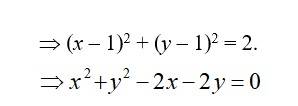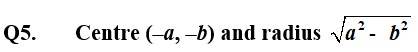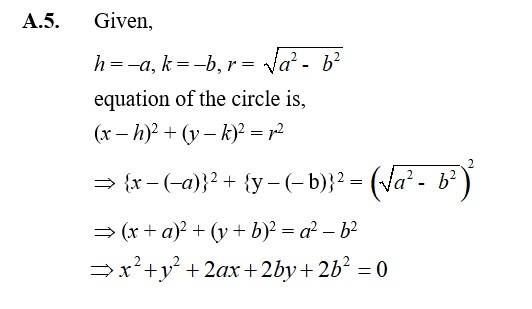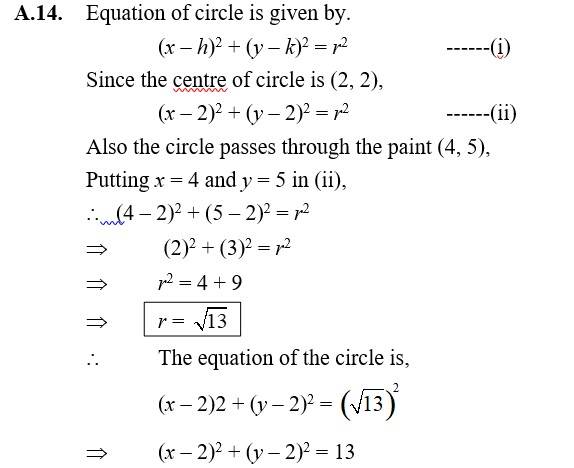Conic Sections Class 11 NCERT Solutions is an important chapter of Mathematics. It covers the following curves: circles, parabolas, ellipses, and hyperbolas. These curves are called the conic sections or conics. These curves have a variety of applications in fields such as reflectors in flashlights, the design of telescopes and antennas, planetary motion, and automobile headlights.
The experts at Shiksha designed the Conic Sections Class 11. The study material is accurate and reliable. It can help students improve their problem-solving skills. There is also a free Conic Sections Class 11 PDF link given on this page, which students can download.
If you want chapter-wise Class 11 Maths NCERT Notes with solved examples and important topics, Explore Here.
- Summary of Conic Sections Class 11 Mathematics
- Class 11 Math Conic Section: key Topics, Weightage
- Important Formulas of Class 11 Maths Chapter 10 Conic Sections
- Class 11 Math Conic Section NCERT Solution PDF: Download Free PDF
- Class 11 Math Conic Section: Exercise-wise Solutions
- Class 11 Math Conic Section Exercise 10.1 Solutions
- Class 11 Math Conic Section Exercise 10.2 Solutions
- Class 11 Math Conic Section Exercise 10.3 Solutions
- Class 11 Math Conic Section Exercise 10.4 Solutions
- Class 11 Math Conic Section Miscellaneous Exercise Solution
- Conic Sections - FAQs
Summary of Conic Sections Class 11 Mathematics
Here is a quick summary of the Conic Sections Class 11 Solutions:
- It covers circle, which is the set of all points in a plane that are at an equal distance from a fixed point in a plane. Mathematically, a circle's equation with centre (h,k), and radius r is:
- It defines parabola, it is a set of all points in a plane at an equal distance from a fixed point and a fixed line in the plane. The parabola with focus at (a, 0) a > 0 and directrix x = – a is:
- Chapter 10 Class 11 Mathematics also covers latus rectum, ellipse, and latus rectum of ellipse.
To get access to the quick NCERT revision notes of Class 11 of Physics, Chemistry and Maths, do check out here.
Class 11 Math Conic Section: key Topics, Weightage
NCERT Solutions Conic Sections Class 11 Mathematics is an important chapter for entrance exams. Coordinate geometry, which is part of conic sections, is significant in JEE Main and carries a high weightage of around 15-20%. The following are the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 10.1 | Introduction |
| 10.2 | Sections of a Cone |
| 10.3 | Circle |
| 10.4 | Parabola |
| 10.5 | Ellipse |
| 10.6 | Hyperbola |
Conic Sections Class 11 Weightage in JEE Main
| Exams | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 2-5 questions | 9.9% |
Important Formulas of Class 11 Maths Chapter 10 Conic Sections
Important Formulae of Conic Sections for CBSE and JEE Mains
Circle
- General Form:
where (0,0) is the center, and r is the radius.
- Equation with Center (h, k) and Radius r:
- General Equation of a Circle:
where:
-
- Center =
- Radius =
- Equation of a Tangent to a Circle
- Tangent at a Point on the Circle:
- Equation of Normal to a Circle
A normal at a point on the circle passes through the center, so its equation is:
Parabola
- Standard Parabola Equation:
- Parametric Form:
- Tangent Equation:
- Normal Equation:
- Length of Latus Rectum:
- Condition for Tangency:
Hyperbola
- Standard Hyperbola Equation:
- Parametric Form:
- Tangent Equation:
- Equation of Asymptotes:
- Eccentricity:
Class 11 Math Conic Section NCERT Solution PDF: Download Free PDF
To get the free Conic Sections Class 11 PDF, students must click the link given below. It contains solutions to all the NCERT questions. By practicing these solutions, the students will understand how to solve complex questions and will gain confidence to score high in the CBSE Board exam and other competitive exams like JEE Main exams.
Class 11 Math Chapter 11 Conic Section Solution: Download Free PDF
Related Links
| NCERT Solutions for Class 12 Physics | NCERT Notes for Class 11 & 12 |
| NCERT Solutions for Class 11 Maths | NCERT Solutions Class 11 and 12 for Maths, Physics, Chemistry |
Class 11 Math Conic Section: Exercise-wise Solutions
Coni Section is one of the most vital chapters to build an advanced understanding of 2D and 3D geometry. This chapter helps Students to understand all the sections that could be possible by cutting a cone in different ways. The Conic section chapter in class 11 NCERT Mathemtics primarily contains concepts related to circles, ellipses, parabolas, and hyperbolas. Students will get problems based on the concepts of conic sections, such as let's rectum, dirctix, general form, standard form of circle, parabola, ellipse and hyperbola, and more. Students can access the solutions to all the exercises below. Class 11 Math conic section is now numbered as chapter 10 earlier, it used to be chapter 11. Check out the solutions below;
Class 11 Math Conic Section Exercise 10.1 Solutions
Conic Section Exercise 10.1 focuses on concepts related to the circle and its properties. Ex 10.1 Conic section focuses on the general equation (form) of a conic section, Radius, Center, Chord, Secant and its equation, Tangent and its equation, and more. Students can check the solution and learn the details of problem-solving for concepts related to circles. The conic section ex 10.1 consists of 15 questions, mostly short-answer type. Find the Class 11 Math conic section ex 10.1 solution below;
Class 11 Conic Section Exercise 10.1 SolutionIn each of the following Exercises, 1 to 5, find the equation of the circle with Q1. centre (0,2) and radius 2 |
| A.1. Centre (0, 2) and radius 2 . Here, h = 0, k = 2, r = 2 The equation of the circle is given by' (x – h)2 + (y – k)2 = r2 x2 + (y – 2)2 = 4
|
| Q2.centre (–2,3) and radius 4 |
| A.2. Centre (–2, 3) and radius 4. Given, h = –2, k = 3, r = 4 ⸫ Equation of the circle is, (x – h)2 + (y – k)2 = 22 (x + 2)2 + (y – 3)2 = 16
|
| Q3.Centre and radius |
| A.3. Given, h = , k = , r = ⸫ Equation of the circle is, (x – h)2 + (y – k)2 = r2
|
| Q4. centre (1,1) and radius |
| In each of the following Exercises 6 to 9, find the centre and radius of the circles. Q6. (x + 5)2 + (y – 3)2 = 36 |
| Q7. x2 + y2 – 4x – 8y – 45 = 0 |
| Q8. x2 + y2 – 8x + 10y – 12 = 0 |
| Q9. 2x2 + 2y2 – x = 0 |
| A.9. 2x2 + 2y2= x 2(x2 + y2) = x x2 + y2 = x2 – + y2= 0 x2 – 2 + y2 = 0 x2 – x2 – Using, (a – b)2 = a2 + b2 – 2ab, We get
Comparing with the equation of a circle (x – h)2 + (y – k)2 = r2 We get, h = , k = 0, r = ⸫Centre = (h, k) = Radian = r = |
| Q10. Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16. |
| A.10. Let the equation of the circle be, (x – h)2 + (y – k)2 = r2 -------(i) Since the circle passes through (4, 1) and (6, 5) Putting x = 4 and y = 1 in (i), (4 – h)2 + (1 – k)2 = 22 ---------(ii) Putting x = 6 and y = 5 in (i), (6 – h)2 + (5 – k)2 = r2---------(iii) Equating equation (ii) and (iii), We get. (4 – h)2 + (1 – k)2 = (6 – h)2 + (5 – k)2 42 + h2 – 2.4.h + 12 + k2 – 2.1.k = 62 + h2 – 2.6.h + 52 + k2 – 2.5.k 16 + h2 – 8h + 1 + k2 – 2k = 36 + h2 – 12h + 25 + k2 – 10k 17 + h2 – 8h + k2 – 2k = 61 + h2 – 12h + k2 – 10k –8h + 12h – 2k + 10k = 61 – 17 4h + 8k = 44 4(h + 2k) = 44 h + 2k = = 11-------------(iv) Since the centre of the circle passes through 4x + y = 16 ⸫4h + k = 16 (4h + k = 16) × 2 8h + 2k = 32--------------(v) Subtract (v) – (iv). 8h + 2k = 32 –(h + 2k = 11) 7h = 21 h = = 3 Putting h = 3 in (iv), we get 3 + 2k = 11 2k = 11 – 3 k = = 4 Putting the values of h and k in, (ii) (4 – 3)2 + (1 – 4)2 = r2 12 + (–3)2 = r2 1 + 9 = r2 r = √10 Thus the equation of the circle is, (x – 3)2 + (y – 4)2 = (x – 3)2 + (y – 4)2 = 10 x2 |
| Q11. Find the equation of the circle passing through the points (2,3) and (–1,1) and whose centre is on the line x – 3y – 11 = 0. |
| A.11. Let the equation of the circle be. (x – h)2 + (y – k)2 = r2 -----(i) Since the circle passes through (2, 3) and (–1, 1), Putting x = 2 and y = 3 in (i), (2 – h)2 + (3 – k)2 = r2---------(ii) Putting x = –1 and y = 1 in (i), (–1 – h)2 + (1 – k)2 = r2 Equating equation (ii) and (iii), We get:– (2 – h)2 + (3 – k)2 = (–1 – h)2 + (1 – k)2 22 + h2 – 2.2.h + 32 + k2 – 2.3.k = (–1)2 + h2 – 2.(–1).h + 12 + k2 – 2(1)(k) 4 + h2 – 4h + 9 + k2 – 6k = 1 + h2 + 2h + 1 + k2 – 2k 13 – 4h – 6k = 2 + 2h – 2k –4h – 2h – 6k + 2k = 2 – 13 –6h – 4k = 11 –(6h + 4k) = 11 6h + 4k = 11-------(iv) Since the centre of the circle is on the line x – 3y – 11 = 0 ⸫ h – 3k = 11 (h – 3k = 11) × 6 = 6h – 18k = 66-----(v) Subtract (v) – (iv),
– 22k = 55 k = Putting the value of k in (iv), we get 6h + × 6h + 6h = 11 + 6h = 11 + 10 h = Putting values of h and k in (ii), we get
r2 = r2 = r = Than the equation of the circle is,
|
| Q12. Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2,3). |
| A.12. Given, r = 5. Since the centre lies on x – axis. k = 0. ⸫Centre of circle = (h, k) = (h, 0) The equation of the circle in given by, (x – h)2 + (y – k)2 = r2 (x – h)2 + (y – 0)2 = (5)2 (x – h)2 + y2 = 25--------(i) Since the curie parses through the point (2, 3), Putting x = 2 and y = 3 in equation (1), We get. (2 – h)2 + (3)2 = 25 22 + h2 – 22.h + 9 = 25 4 + h2– 4h + 9 = 25 h2 – 4h + 13 – 25 = 0 h2 – 4h – 12 = 0 h2 – (6 – 2)h – 12 = 0 h2 – 6h + 2h – 12 – 0 h(h – 6) + 2(h – 6) = 0 (h – 6)(h + 2) = 0 h = 6 and h = –2 When h = 6, From (i), Equation of circle is, (x –6)2 + y2 = 25 (x – 6)2 + (y – 0)2 = 52 When h = –2, Equation of circle is, (x + 2)2 + (y – 0)2 = 52 or x2 |
| Q13. Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes. |
| A.13. Let the equation of the circle be, (x – h)2 + (y – k)2 = r2 – 0-----(i) As the circle is passing through (0, 0) we get, (0 – h)2 + (0 – k)2 = r2 (–h)2 + (–k)2 = r2 h2 + k2 = r2--------(ii) The circle also makes intercepts a and b on the cooperate axes. Let intercept on x–axis be 'a' and on y–axis be 'b' ⸫Circle also passes through (a, 0) and (0, b) Putting x = a and y = 0 in (i) (a – h)2 + (0 – k)2 = r2 a2 + h2 – 2.a.h + (–k)2 = r2 a2 – 2ah + h2 + k2 = r2 Putting value of r2 from (ii), we get a2 – 2ah + h2 + k2 = h2 + k2 a2 = 2ah a = 2h h = Putting x = 0 andy = b in (i). (0 – h)2 + (b – k)2 = r2 h2 + b2 + k2 – 2bk = r2 Putting value of r2 from (ii), h2 + b2 + k2 – 2bk = h2 + k2 b2 = 2bk b = 2k k = Putting values of h and k in (ii),
r2 = Putting the values of h1 k and r2 in (i),
x2 + – 2.x. + y2 + – 2 .y. = x2 + – ax + y2 + – yb = ⸫The equation of the circle is, x2 – ax + y2 – by = 0 |
| Q14. Find the equation of a circle with centre (2,2) and passes through the point (4,5). |
|
|
| Q15. Does the point (–2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25? |
Commonly asked questions
Class 11 Conic Section Exercise 10.2 Solution
In each of the following Exercises 16 to 22, find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.
16. y2 = 12x
16. Centre (0, 2) and radius 2 .
Here, h = 0, k = 2, r = 2
The equation of the circle is given by'
(x – h)2 + (y – k)2 = r2
x2 + (y – 2)2 = 4
11. Find the equation of the circle passing through the points (2,3) and (–1,1) and whose centre is on the line x – 3y – 11 = 0.
11. Let the equation of the circle be.
(x – h)2 + (y – k)2 = r2 -----(i)
Since the circle passes through (2, 3) and (–1, 1),
Putting x = 2 and y = 3 in (i),
(2 – h)2 + (3 – k)2 = r2---------(ii)
Putting x = –1 and y = 1 in (i),
(–1 – h)2 + (1 – k)2 = r2
Equating equation (ii) and (iii), We get:–
(2 – h)2 + (3 – k)2 = (–1 – h)2 + (1 – k)2
22 + h2 – 2.2.h + 32 + k2 – 2.3.k = (–1)2 + h2 – 2.(–1).h + 12 + k2 – 2(1)(k)
4 + h2 – 4h + 9 + k2 – 6k = 1 + h2 + 2h + 1 + k2 – 2k
13 – 4h – 6k = 2 + 2h – 2k
–4h – 2h – 6k + 2k = 2 – 13
–6h – 4k = 11
–(6h + 4k) = 11
6h + 4k = 11-------(iv)
Since the centre of the circle is on the line x – 3y – 11 = 0
? h – 3k = 11
(h – 3k = 11) × 6 = 6h – 18k = 66-----(v)
Subtract (v) – (iv),
– 22k = 55
k =
Putting the value of k in (iv), we get
6h + ×
6h +
6h = 11 +
6h = 11 + 10
h =
Putting values of h and k in (ii), we get
r2 =
r2 =
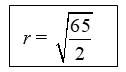
Than the equation of the circle is,
18. y2 = –8x
18. y2 = –4ax
Comparing with the given equation y2 = –8x
We get,
–4ax = –8x
a =
? Co–ordinates of focus is (–0, 0) = (–2, 0)
Axis of Parabola : x-axis.
Equation of directrix is,
x = a
x = 2
Length of latus rectum =4a
= 4 × 2 = 8
23. Four (0, –3); directrix y = 3.
23. Since the focus (0, –3) lies on the y–axis, the y–axis is the axis of parabola.
Hence the equation is either x2 = 4ay or x2 = –4ay
Since the directrix is y = 3 and the forces (0, –3) has negative y Co–ordinate.
The equation must be
x2 = –4ay
Co–ordinate of focus = (0, –a)
(0, –a) = (0, –3)
–a = –3
a = 3
? Equation of parabola is
x2 = –4ay
x2 = –4 (3)y
x2 = –12y
26. Vertex (0, 0) passing through (2, 3) and axis is along x-axis
26. Since the axis of parabola is x-axis,
The equation parabola is either y2 = 4ax or y2 = 4ax.
Also it passes through (2, 3) which lies in the first quadrant.
So the equation is,
y2= 4ax
Putting x = 2 and y = 3, we set
(3)2 = 4 (a) (2)
a =
? The equation of parabola is y2 = 4
y2 =
2y2 = 9x
27. Vertex (0, 0) passing through (5, 2) and symmetric with respect to y-axis
27. Since the parabola is symmetric with respect to y-axis and has vertex (0, 0)
The equation in of the form x3 = 4ay or x2 = 4ay.
The parabola passes through (5, 2) which lies on the 1st quadrant
? The equation of parabola is of the form,
x2 = 4ay
Putting x = 5 and y = 2,
(5)2 = 4 (a) (2)
25 = 8a
a =
? The equation of the parabola is,
x2 = 4ay
2x2 = 25y
Class 11 Conic Section Exercise 10.1 Solution
In each of the following Exercises, 1 to 5, find the equation of the circle with
1. centre (0,2) and radius 2
1. Centre (0, 2) and radius 2 .
Here, h = 0, k = 2, r = 2
The equation of the circle is given by'
(x – h)2 + (y – k)2 = r2
x2 + (y – 2)2 = 4
2. Centre (–2,3) and radius 4
2. Centre (–2, 3) and radius 4.
Given, h = –2, k = 3, r = 4
? Equation of the circle is,
(x – h)2 + (y – k)2 = 22
(x + 2)2 + (y – 3)2 = 16
3. Centre and radius
3. Given,
h = , k = , r =
? Equation of the circle is,
(x – h)2 + (y – k)2 = r2
9. 2x2 + 2y2 – x = 0
9. 2x2 + 2y2= x
2(x2 + y2) = x
x2 + y2 =
x2 – + y2= 0
x2 – 2 + y2 = 0
x2 –
x2 –
Using,
(a – b)2 = a2 + b2 – 2ab,
We get
Comparing with the equation of a circle (x – h)2 + (y – k)2 = r2
We get,
h = , k = 0, r =
?Centre = (h, k) =
Radian = r =
10. Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16.
10. Let the equation of the circle be,
(x – h)2 + (y – k)2 = r2 - (i)
Since the circle passes through (4, 1) and (6, 5)
Putting x = 4 and y = 1 in (i),
(4 – h)2 + (1 – k)2 = 22 - (ii)
Putting x = 6 and y = 5 in (i),
(6 – h)2 + (5 – k)2 = r2- (iii)
Equating equation (ii) and (iii), We get.
(4 – h)2 + (1 – k)2 = (6 – h)2 + (5 – k)2
42 + h2 – 2.4.h + 12 + k2 – 2.1.k = 62 + h2 – 2.6.h + 52 + k2 – 2.5.k
16 + h2 – 8h + 1 + k2 – 2k = 36 + h2 – 12h + 25 + k2 – 10k
17 + h2 – 8h + k2 – 2k = 61 + h2 – 12h + k2 – 10k
–8h + 12h – 2k + 10k = 61 – 17
4h + 8k = 44
4 (h + 2k) = 44
h + 2k = = 11- (iv)
Since the centre of the circle passes through 4x + y = 16
? 4h + k = 16
(4h + k = 16) × 2
8h + 2k = 32- (v)
Subtract (v) – (iv).
8h + 2k = 32
– (h + 2k = 11)
7h = 21
h = = 3
Putting h = 3 in (iv), we get
3 + 2k = 11
2k = 11 – 3
k = = 4
Putting the values of h and k in, (ii)
(4 – 3)2 + (1 – 4)2 = r2
12 + (–3)2 = r2
1 + 9 = r2
r = √10
Thus the equation of the circle is,
(x – 3)2 + (y – 4)2 =
(x – 3)2 + (y – 4)2 = 10
x2
12. Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2,3).
12. Given,
r = 5.
Since the centre lies on x – axis.
k = 0.
? Centre of circle = (h, k) = (h, 0)
The equation of the circle in given by,
(x – h)2 + (y – k)2 = r2
(x – h)2 + (y – 0)2 = (5)2
(x – h)2 + y2 = 25- (i)
Since the curie parses through the point (2, 3),
Putting x = 2 and y = 3 in equation (1), We get.
(2 – h)2 + (3)2 = 25
22 + h2 – 22.h + 9 = 25
4 + h2– 4h + 9 = 25
h2 – 4h + 13 – 25 = 0
h2 – 4h – 12 = 0
h2 – (6 – 2)h – 12 = 0
h2 – 6h + 2h – 12 – 0
h (h – 6) + 2 (h – 6) = 0
(h – 6) (h + 2) = 0
h = 6 and h = –2
When h = 6,
From (i), Equation of circle is,
(x –6)2 + y2 = 25
(x – 6)2 + (y – 0)2 = 52
When h = –2,
Equation of circle is, (x + 2)2 + (y – 0)2 = 52 or x2 +2
13. Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
13. Let the equation of the circle be,
(x – h)2 + (y – k)2 = r2 – 0-----(i)
As the circle is passing through (0, 0) we get,
(0 – h)2 + (0 – k)2 = r2
(–h)2 + (–k)2 = r2
h2 + k2 = r2--------(ii)
The circle also makes intercepts a and b on the cooperate axes.
Let intercept on x–axis be 'a' and on y–axis be 'b'
?Circle also passes through (a, 0) and (0, b)
Putting x = a and y = 0 in (i)
(a – h)2 + (0 – k)2 = r2
a2 + h2 – 2.a.h + (–k)2 = r2
a2 – 2ah + h2 + k2 = r2
Putting value of r2 from (ii), we get
a2 – 2ah + h2 + k2 = h2 + k2
a2 = 2ah
a = 2h
h =
Putting x = 0 andy = b in (i).
(0 – h)2 + (b – k)2 = r2
h2 + b2 + k2 – 2bk = r2
Putting value of r2 from (ii),
h2 + b2 + k2 – 2bk = h2 + k2
b2 = 2bk
b = 2k
k =
Putting values of h and k in (ii),
r2 =
Putting the values of h1 k and r2 in (i),
x2 + – 2.x. + y2 + – 2 .y. =
x2 + – ax + y2 + – yb =
?The equation of the circle is,
x2 – ax + y2 – by = 0
22. Focus (6, 0); directrix x = –6.
22. Since the focus (6, 0) lien on the x–axis, the x–axis is the axis of parabola
Hence the equation is either y2 = 4ax or y2 = –4ax
Since the directrix is x = –6 and the focus (6, 0) has positive x – Coordinate,
The equation must be y2 = 4ax
with a = 6
Hence, equation of parabola is,
y2 = 4ax
y2 = 4 (6)x
y2 = 24x
24. Vertex (0, 0); focus (3, 0)
24. Since the focus (3, 0) lies on the x-axis, the x-axis is the axis of parabola.
Hence the equation is either y2 = 4ax or y2 = –4ax
Since the focus has positive x co-ordinate,
The equation must be y2 = 4ax
Co-ordinate of focus (a, 0) = (3, 0)
a = 3
? The equation is given by
y2 = 4 (3)x
y2 = 12x
25. Vertex (0, 0); focus (–2, 0)
25. Focus (-2, 0) lies on x-axis and the x-Co-ordinate is negative.
The equation must be, y2 = 4ax
Co-ordinate of focus = (–a, 0) = (–2, 0)
–a = –2
a = 2
? Equation of a parabola is,
y2 = –4 (2)x
y2 = –8x
Class 11 Math Conic Section Exercise 10.2 Solutions
Conic Section Exercise 10.2 focuses on concepts and properties related to the Parabola. Ex 10.2 Conic Section Class 11 Math Solutions will include problems based on finding focus, axis, directix and equation of directix, latus rectum of parabola, finding equation of parabola when other information is available and more. This Class 111 Math exercise 10.2 includes 12 questions, and their solutions are available below;
Class 11 Conc Section NCERT Solution below;In each of the following Exercises 1 to 6, find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum. Q1. y2 = 12x |
| A.1. y2 = 4ax Comparing with the given equation, y2 = 12x, We get, 4a = 12 a = ⸫Co–ordinates of the focus are (a, 0) = (3, 0) Axis of Parabola : x-axis. Equation, of directrix as, x = –a x = –3 Length of latus rectum = 4a = 4 × 3 = 12 |
| Q2. x2 = 6y |
| A.2. x2 = 4ay. Comparing with the given equation x2 = 6y We get, 4a = 6 a = Co–ordinates of focus are (0, a) = Axis of Parabola : y-axis. Equation of directrix is, y = –a y = – Length of latus rectum =4a = 4 × = 2 × 3 = 6. |
| Q3. y2 = –8x |
| A.3. y2 = –4ax Comparing with the given equation y2 = –8x We get, –4ax = –8x a = ⸫ Co–ordinates of focus is (–0, 0) = (–2, 0) Axis of Parabola : x-axis. Equation of directrix is, x = a x = 2 Length of latus rectum =4a = 4 × 2 = 8 |
| Q4.x2 = –16y |
| A.4. x2 = –4ay Comparing with the given equation x2 = –16y We get, –4a = –16 a = a = 4 Co–ordinate of focus is (0, –a) = (0, –4) Axis of Parabola : y-axis. Equation of directrix is y = a y = 4 Length of latus rectum =4a = 4 × 4 = 16 |
| Q5. y2 = 10x |
| A.5. y2 = 4ax Comparing with the given equation y2 = 10x, We get, 4a = 10 a = a = ⸫ Co–ordinates of focus is (a, 0) = Axis of Parabola : x-axis. Equation of directrix is. x = –a x = Length of latus rectum =4a = = 2 × 5 = 10. |
| Q6.x2 = –9y |
| A.6. The given equation involves x2, so its axis is y–axis. Also the Co–efficient of y is negative. Hence we use the equation, x2 = –4ay Comparing with the given equation x2 = –9y, We get, –4a = –9 a = a = Co–ordinates of focus in (0, –a) = Axis of Parabola : y-axis. equation of directrix is, y = a y = Length of latus rectum =4a = 4 × = 9 In each of the Exercises 7 to 12, find the equation of the parabola that satisfies the given conditions: |
| Q7. Focus (6, 0); directrix x = –6. |
| A.7. Since the focus (6, 0) lien on the x–axis, the x–axis is the axis of parabola Hence the equation is either y2 = 4ax or y2 = –4ax Since the directrix is x = –6 and the focus (6, 0) has positive x – Coordinate, The equation must be y2 = 4ax with a = 6 Hence, equation of parabola is, y2 = 4ax y2 = 4(6)x y2 = 24x |
| Q8. Four (0, –3); directrix y = 3. |
| A.8. Since the focus (0, –3) lies on the y–axis, the y–axis is the axis of parabola. Hence the equation is either x2 = 4ay or x2 = –4ay Since the directrix is y = 3 and the forces (0, –3) has negative y Co–ordinate. The equation must be x2 = –4ay Co–ordinate of focus = (0, –a) (0, –a) = (0, –3) –a = –3 a = 3 ⸫ Equation of parabola is x2 = –4ay x2 = –4(3)y x2 = –12y |
| Q9. Vertex (0, 0); focus (3, 0) |
| A.9. Since the focus (3, 0) lies on the x-axis, the x-axis is the axis of parabola. Hence the equation is either y2 = 4ax or y2 = –4ax Since the focus has positive x co-ordinate, The equation must be y2 = 4ax Co-ordinate of focus (a, 0) = (3, 0) a = 3 ⸫ The equation is given by y2 = 4(3)x y2 = 12x |
| Q10. Vertes (0, 0); focus (–2, 0) |
| A.10. Focus (-2, 0) lies on x-axis and the x-Co-ordinate is negative. The equation must be, y2 = 4ax Co-ordinate of focus = (–a, 0) = (–2, 0) –a = –2 a = 2 ⸫ Equation of a parabola is, y2 = –4(2)x y2 = –8x |
| Q11. Vertex (0, 0) passing through (2, 3) and axis is along x-axis |
| A.11. Since the axis of parabola is x-axis, The equation parabola is either y2 = 4ax or y2 = 4ax. Also it passes through (2, 3) which lies in the first quadrant. So the equation is, y2= 4ax Putting x = 2 and y = 3, we set (3)2 = 4(a) (2) a = ⸫ The equation of parabola is y2 = 4 y2 = 2y2 = 9x |
| Q12. Vertex (0, 0) passing through (5, 2) and symmetric with respect to y-axis |
| A.12. Since the parabola is symmetric with respect to y-axis and has vertex (0, 0) The equation in of the form x3 = 4ay or x2 = 4ay. The parabola passes through (5, 2) which lies on the 1st quadrant ⸫ The equation of parabola is of the form, x2 = 4ay Putting x = 5 and y = 2, (5)2 = 4(a) (2) 25 = 8a a = ⸫ The equation of the parabola is, x2 = 4ay
2x2 = 25y, |
Class 11 Math Conic Section Exercise 10.3 Solutions
Class 11 Math Conic Section Exercise 10.4 Solutions
Class 11 Math Conic Section Miscellaneous Exercise Solution
Conic Sections - FAQs
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Binomial Theorem
- Probability
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test