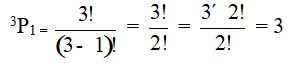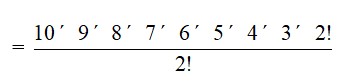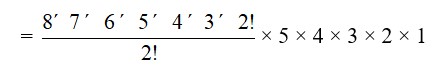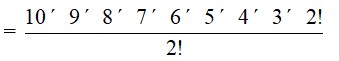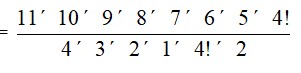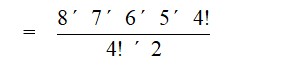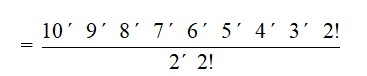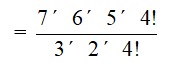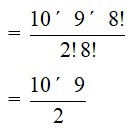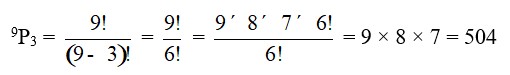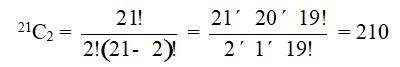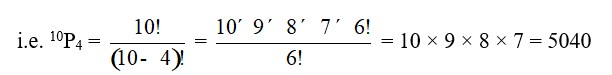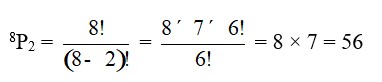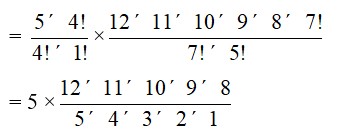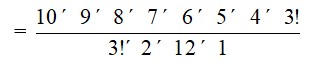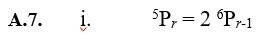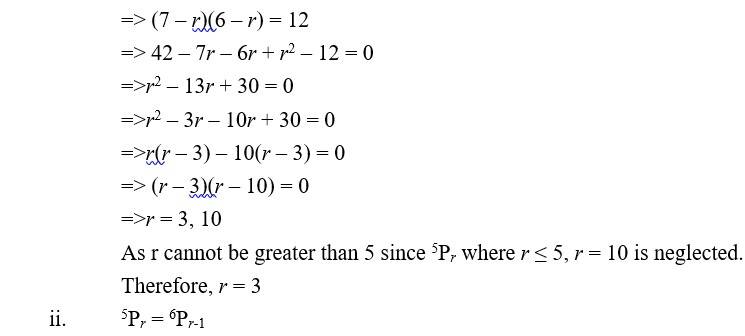Class 11 Permutation and Combination explores the basic counting techniques that help students find many ways of arranging and selecting objects without listing all possible sequences. The chapter covers the fundamentals of counting, including permutations and combinations. Permutation and Combination Class 11 is designed by the subject matter experts at Shiksha to help students deepen their understanding of the concepts. According to this chapter, if an event can occur in x different ways, and another event can occur in y different ways, the total number of events can be given by -
.
The solutions will help them improve their problem-solving skills and boost their confidence in solving the complex questions of this chapter. The step-by-step solutions will help students to score high in the Class 11 exams, CBSE Board, and entrance exams like NEET and JEE Main.
To access the chapter-wise Class 11 Maths NCERT Notes with important topics and solved examples, students can check here. It will provide them with comprehensive notes for Class 11 Maths.
Related Links
| NCERT Notes for Class 11 & 12 | NCERT Solutions for Class 11 Maths | NCERT Solutions Class 11 and 12 for Maths, Physics, Chemistry |
- Overview of Permutations and Combinations Class 11
- Class 11 Permutation and Combinations: Key Topics, Weightage
- Important Formulas of Permutation and Combination Class 11
- Class 11 Permutation and Combinations NCERT Solution PDF: Download PDF for Free
- Class 11 Permutation and Combinations Exercise 6.1 Solutions
- Class 11 Permutation and Combinations Exercise 6.2 Solutions
- Class 11 Permutation and Combinations Exercise 6.3 Solutions
- Class 11 Permutation and Combinations Exercise 6.4 Solutions
- Class 11 Permutation and Combinations Miscellaneous Exercise Solutions
Overview of Permutations and Combinations Class 11
Here is a quick summary of the Class 11 Permutation and Combination:
- It covers the fundamental principle of counting. It says that if an event can occur in x different ways, and after this, another event can occur in y ways, then the total number of events can occur in the following times -
- If P denotes the number of permutations of n different things taken r at a time, P is mathematically shown as -
- Here, p1 objects are of one kind, and p2 objects are of another kind.
- The number of combinations of n different things taken r at a time -
Class 11 Permutation and Combinations: Key Topics, Weightage
A proper understanding of the concepts of Permutations and Combinations Class 11 is important as it forms the basis for probability and other advanced topics in Mathematics. The chapter is also significant for its real-life problem-solving applications. See below the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 6.1 | Introduction |
| 6.2 | Fundamental Principle of Counting |
| 6.3 | Permutations |
| 6.4 | Combinations |
Class 11 Permutation and Combination Weightage in JEE Mains
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Mains | 1 Question | 3.33% |
Important Formulas of Permutation and Combination Class 11
Important Formulae in Permutations and Combinations for CBSE and Competitive Exams
Permutations (Arrangements)
- Permutation Formula:
- Permutation with Repetition:
-
- Permutation of Identical Objects:
- Circular Permutations:
- (for distinct objects in a circle)
- (if clockwise & anti-clockwise arrangements are identical)
Combinations (Selections)
- Combination Formula:
- Properties of Combinations:
-
-
and
- Pascal’s Identity:
-
Special Counting Cases
- Total ways to arrange
distinct objects:
- Total ways to distribute
identical objects among
people:
-
- Total ways to divide
objects into
groups:
- (where are sizes of groups)
Class 11 Permutation and Combinations NCERT Solution PDF: Download PDF for Free
It is recommended for students to download the Permutation and Combination Class 11 Solutions PDF from the link given below. The solutions help students to understand the concepts properly. Explore here the quick revision notes of Class 11 for the subjects Physics, Chemistry, and Maths. These notes help in creating a basic foundation for CBSE Class 12 and competitive exams.
Class 12 Math Chapter 6 Permutation and Combination Solution PDF: Free PDF Download
Class 11 Permutation and Combinations Exercise 6.1 Solutions
Permutations and Combinations Exercise 6.1 of Class 11 Math dives into the basics of Permutations and Combinations such as the Principle of Counting, the basics of arrangements and selections. exercise 6.1 covers essential topics such as the Addition Principle and Multiplication Principle, which help determine the number of ways. There are 6 short answer questions in Class 11 Permutations and Combinations Ex 6.1. Find the Solutions below;
Permutation and Combination Exercise 6.1 SolutionsQ1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed? |
| A.1. i.Since repetition of number is allowed and there are five numbers which can be used to form the necessary 3-digit numbers we can have five numbers that can fill the ones, tens and hundreds place. So, total number of possible 3-digit number = 5 × 5 × 5 = 125 ii.Since repetition of number is not allowed. There are total 5 numbers which can fill the ones places then 4 and 3 numbers which can fill the tens and hundreds place simultaneously. So, total number of possible 3-digit number = 3 × 4 × 5 = 60 |
| Q2. How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated? |
| A.2. Since we are given with six numbers (1, 2, 3, 4, 5, 6) to form 3-digit even number and also repetition is allowed. We can have only the number 2, 4, 6 in the ones place and all the six numbers can fill the tens and hundreds place. So, total number of 3-digit even number that can be formed by 1, 2, 3, 4, 5, 6 = 6 × 6 × 3 = 108 |
| Q3. How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated? |
| A.3. To form a 4-letter code using the first 10 letters of the English alphabet without repeating we can have 10, 9, 8 and 7 numbers of letters to be filled at ones, tens, hundreds and thousands place simultaneously. Hence, total no. of 4-letter code that can be made using the first 10-letter of English alphabet = 7 × 8 × 9 × 10 = 5040 |
| Q4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once? | |||||
| A.4. For the 5-digit telephone number that can be constructed using 0 to 9 if each number starts with 67 and no digit appears more than once we can have
So total number of possible combination = 1 × 1 × 6 × 7 × 8 = 336 |
| Q5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there? |
| A.5. When a coin is tossed one time a head or a tail is the possible outcome. So, when a coin is tossed 3 times the total number of possible outcomes = 2 × 2 × 2 = 8 |
| Q6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other? |
| A.6. To generate a signal which requires 2 flags one below another we can have the following combination of any of the 5 flag at top and the one of the remaining 4 flag at the bottom. Hence, total no. of possible combination = 5 × 4 = 20 |
Commonly asked questions
Permutation and Combinations Miscellaneous Exercise Solutions
32. How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER ?
32. In the word DAUGHTER, there are 3 vowels, namely A, U, E and 5 consonants, namely D, G, H, T, R.
The number of ways of selecting 2 vowels out of 3
= 3C2
=

= 3
The number of ways of selecting 3 consonants out of 5
= 5C3
=
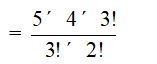
= 5 × 2
= 10
Therefore, the number of combination of 3 consonants and 2 vowels is 3 × 10 = 30.
Each of these 30 combinations has 5 letters which can be arranged among themselves in 5! Ways.
Therefore, the required numbers of different words is
= 30 × 5! = 30 × 5 × 4 × 3 × 2 × 1 = 3600
2. How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
2. Since we are given with six numbers (1, 2, 3, 4, 5, 6) to form 3-digit even number and also repetition is allowed.
We can have only the number 2, 4, 6 in the ones place and all the six numbers can fill the tens and hundreds place.
So, total number of 3-digit even number that can be formed by 1, 2, 3, 4, 5, 6
= 6 * 6 * 3
= 108
33. How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
33. In the word EQUATION, there are vowels (E, U, A, I, O) and 3 consonants (Q, T, N).
Treating vowels as a whole as 1st object and consonants as a whole as 2nd object, we can have an arrangement of 2! = 2.
Similarly, arrangement within the vowels = 5! = 5 * 4 * 3 * 2 * 1 = 120
And arrangement within the consonants = 3! = 3 * 2 * 1 = 6
Therefore, total number of possible arrangement = 2 * 120 * 6 = 1440
14. How many 3-digit even numbers can be made using the digits1, 2, 3, 4, 6, 7, if no digit is repeated?
14. The permutation of having even number at the last digit from the given 6 different digits namely 1, 2, 3, 4, 5, 6 to form a 3-digit number is
After taking one of the even number as last digit we can rearrange the remaining 5 digits taking 2 at a time. i.e.
Therefore, The required number = 20 × 3 = 60
22. In how many ways can the letters of the word PERMUTATIONS be arranged if the
(i) Words start with P and end with S,
(ii) Vowels are all together,
(iii) Thereare always 4 letters between P and S?
22. There are 12 letters in which T appears 2 times and rest are all different.
i. When P and S are fixed as first and last letter we can arrange the remaining 10 letter taking all at a time. i.e.
Number of permutation =
= 18,14,400
ii. We take the 5 vowels (E, U, A, I, O) as one single object. This single object with the remaining 7 object are treated as 8 object which have 2 – T's.
So, number of permutations in which the vowels come together
= permutation of 8 object x permutation within the vowels
= * 5!
= 20160 * 120
= 2419200
iii. In order to have 4 letters between P and S, (P, S) should have the possible sets of places (1, 6), (2, 7), (3, 8), (4, 9), (5, 10), (6, 11) and (7, 12) similarly (S, P) should have the same possible sets of places.
So, total number of possible positions fixed for P and S = 14
After fixing P and S we can rearrange the remaining 10 places with the remaining 10 letters of which 2 are T's.
So, required permutation =
= 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3
= 18,14,400
Therefore, total permutation for which there are always 4 letters between P and S
= 14 * 18,14,400
= 2,54,01,600
28. Determine the number of 5 card combinations out of a deck of 52 cards if thereis exactly one ace in each combination.
28. In a deck of 52 cards there are 4 ace cards. The required number of ways of selecting one ace card from the four = 4C1 = = = = 4
After selecting one ace we need to select the remaining 4 card from the remaining 48 card to have a combination of 5 cards. The required number of ways
= 48C4
=

= 1,94,580
Therefore, the total number of ways for selecting 5 card combination out of a deck of 52 cards if there is exactly one ace in each combination
= 4C1×48C4
= 4 × 1,94,580
= 7,78,320
10. If , find x
10. We have,
+ =
=> + =
=> 1 + =
=> =
=>x = 8 * 8
=>x = 64
Permutation and Combination Exercise 6.1 Solutions
1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
1. i. Since repetition of number is allowed and there are five numbers which can be used to form the necessary 3-digit numbers we can have five numbers that can fill the ones, tens and hundreds place.
So, total number of possible 3-digit number = 5 * 5 * 5 = 125
ii. Since repetition of number is not allowed. There are total 5 numbers which can fill the ones places then 4 and 3 numbers which can fill the tens and hundreds place simultaneously.
So, total number of possible 3-digit number = 3 * 4 * 5 = 60
21. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
21. There are 11 letters of which M appears 1 time, I appears 4 times, S appears 4 times and P appears 2 times.
The required number of arrangements =
= 11 * 10 * 9 * 5
= 34650
When the four I occurs together we treat them as single object IIII. This single object together with 7 remaining object will account for 8 object which have 1-M. 2-P and 4-S.
So, required number of permutation =
= 840
Therefore, total no. of permutation in which 4-I's do not come together
= 34650 – 840
= 33810
34. If the different permutations of all the letter of the word EXAMINATION arelisted as in a dictionary, how many words are there in this list before the firstword starting with E ?
34. In the eleven-letter word EXAMINATION there are 2A's, 2I's and 2N's and the rest are all different.
Since in a dictionary the words are listed according to the English alphabet we can only find words starting with A (as B, C, D are not a part of the letters forming the word EXAMINATION) listed before E.
Hence after fixing one A as first word we can rearrange the remaining 10 letters of which 2 are I, 2 are N and rest are all different.
Therefore, the required number of ways =
= 10 * 9 * 8 * 7 * 6 * 5 * 2 * 3
= 9,07,200
39. It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
39. As out of the total 9 seats 4 women are to be at even places we can have the following arrangement.
Seat places
| M | W | M | W | M | W | M | W | M |
Seat places | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th |
Also from this arrangement the women and men can rearrange among themselves.
Therefore, the required number of ways = 4! * 5!
= (4 * 3 * 2 * 1) * (5 * 4 * 3 * 2 * 1)
= 24 * 120
= 2880
27. Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5blue balls if each selection consists of 3 balls of each colour.
27. Since we are to select 3 balls from each colour in order to select 9 balls from the collections of 6, 5 and 5 balls of red, white and blue colours respectively, we can have the combination
6C3 (red) ×5C3 (white) ×5C3 (blue)
= × ×
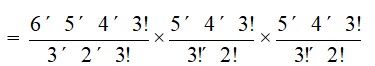
= 20 × 10 × 10
= 2000
31. In how many ways can a student choose a programme of 5 courses if 9 coursesare available and 2 specific courses are compulsory for every student?
31. A student can choose 5 out of 9 available courses. However 2 specific courses are made compulsory.
So, now a student has 3 choices out of the remaining 7 courses.
Therefore, the required number of ways
=7C3
=
= 35
35. How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7 and 9 which are divisible by 10 and no digit is repeated ?
35. Since the 6-digit numbers to be formed from the digits 0, 1, 3, 5, 7 and 9 has to be divisible by 10 we have to fix the unit place as 0. Now, the remaining 5 places can be filled only by the digits 1, 3, 5, 7 and 9.
Therefore, the required number of ways
= 5!
= 5 * 4 * 3 * 2 * 1
= 120
36. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?
36. In an English word there are 5 vowels and 21 consonants.
The number of ways of selecting 2 vowel out of 5 = 5C2
=
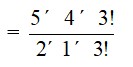
= 5 * 2 = 10
The number of ways of selecting 2 consonants out of 21 = 21C2
=
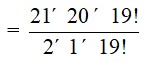
= 21 * 10
= 210
Therefore, the number of combinations of 2 vowels and 2 consonants is 10 * 210 = 2100
Each of these 2100 combinations has 4 letters which can be rearranged among themselves in 4! Ways.
Therefore, the required number of ways
= 4! * 2100
= 4 * 3 * 2 * 1 * 2100
= 50400
20. How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but first letter is a vowel?
20. i. The permutation of 6 letters in MONDAY taken 4 at a time without repetition is
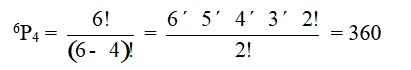
ii. The permutation of 6 letters in MONDAY when all letters are taken at a time is
6P6 = = = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
iii. The permutation of having one of the two vowels (O, A) as first letter from the word MONDAY when all letters are taken at a time is
2P1 = = 2
After fixing one of the vowel as first letter we can rearrange the remaining 5 letters taking 5 at a time
5P5 = = = 5! = 5 × 4 × 3 × 2 × 1 = 120
Therefore, total permutation when all letters are used but first letter is vowel from the word MONDAY = 2 × 120 = 240
Class 11 Permutation and Combinations Exercise 6.4 Solutions
23. nC8 = nC2, find nC2.
23. nC8 = nC2
As, nCa = nCb
=>a = b or a = n – b
=>n = a + b
We have,
nC8 = nC2
=>n = 8 + 2
=>n = 10
Therefore,
nC2
= nC2
=
=
= 45
Permutations and Combinations Exercise 6.3 Solutions
12. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
12. The permutation of 9 different digits taken 4 at a time is given by
25. How many chords can be drawn through 21 points on a circle?
25. A chord is drawn by connecting 2 points on a circle.
As we are given with 21 points on the circle, we have the following combination to find the number of chords.
8. Is 3 ! + 4 ! = 7 ! ?
8. L.H.S = 3! + 4!
= (1 × 2 × 3) + (1 × 2 × 3 × 4)
= 6 + 24
= 30
R.H.S = 7!
= 1 × 2 × 3 × 4 × 5 × 6 × 7
= 5040
As, L.H.S ≠ R.H.S
3! + 4! ≠ 7!
24. Determine n if (i) 2nC3 : nC3 = 12 : 1 (ii) 2nC3 : nC3 = 11 : 1
24. i. 2nC3 : nC3 = 12 : 1
=> ÷ =
=> × = 12
=> = 12
=> = 12
=> 4(2n - 1) = 12(n – 2)
=> 8n – 4 = 12n – 24
=> 24 – 4 = 12n – 8n
=> 20 = 4n
=>n =
=>n = 5
ii. 2nC3 : nC3 = 11 : 1
=> ÷ =
=> × = 11
=> = 11
=> 4(2n – 1) = 11(n – 2)
=> 8n – 4 = 11n – 22
=> 22 – 4 = 11n – 8n
=> 18 = 3n
=>n =
=>n = 6
9. Compute
9. = = 4 * 7 = 28
13. How many 4-digit numbers are there with no digit repeated?
13. For every four-digit number we have to count the permutation of 10 digits namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 taken 4 at a time
However, these permutation will include those where 0 is at 1000's place.
So, fixing 0 at 1000's place and rearranging the remaining 9 digits taking 3 at a time.
3. How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
3. To form a 4-letter code using the first 10 letters of the English alphabet without repeating we can have 10, 9, 8 and 7 numbers of letters to be filled at ones, tens, hundreds and thousands place simultaneously.
Hence, total no. of 4-letter code that can be made using the first 10-letter of English alphabet = 7 * 8 * 9 * 10 = 5040
4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
4. For the 5-digit telephone number that can be constructed using 0 to 9 if each number starts with 67 and no digit appears more than once we can have
6 | 7 | 6 numbers | 7 numbers | 8 numbers |
So total number of possible combination = 1 * 1 * 6 * 7 * 8 = 336
5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
5. When a coin is tossed one time a head or a tail is the possible outcome.
So, when a coin is tossed 3 times the total number of possible outcomes = 2 * 2 * 2 = 8
6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
6. To generate a signal which requires 2 flags one below another we can have the following combination of any of the 5 flag at top and the one of the remaining 4 flag at the bottom.
Hence, total no. of possible combination = 5 * 4 = 20
Permutation and Combinations Ex 6.2 Solutions
7. Evaluate
(i) 8 !
(ii) 4 ! – 3!
1. We know that, n! = n (n – 1) (n – 2)…….
i. 8!
8! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8
= 40320
ii. 4! – 3!
= (1 * 2 * 3 * 4) – (1 * 2 * 3)
= 24 – 6
= 18
11. Evaluate when (i) n = 6, r = 2 (ii) n = 9, r = 5.
11. i. n = 6, r = 2
=
=
= 30
ii. n = 9, r = 5
=
=
= 9 × 8 × 7 × 6 × 5
= 15,120
15. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4,5 if no digit is repeated. How many of these will be even?
15. The permutation of 5 different digits namely 1, 2, 3, 4, 5 taken 4 at a time is
5P4 = = = 5 × 4 × 3 × 2 × 1 = 120
The permutation of having 2 or 4 at ones place is
2P1 = = = 1 × 2 = 2
After fixing one of the even number at last digit we can rearrange the remaining four digits taking 3 at a time. i.e.
4P3 = = = 4 × 3 × 2 × 1 = 24
Therefore, total permutation of 4 digit even number using 1, 2, 3, 4, 5
= 24 × 2
= 48
16. From a committee of 8 persons, in how many ways can we choose a chairmanand a vice chairman assuming one person can not hold more than one position?
16.The permutation of 8 persons taken 2 positions at a time is
19. How many words, with or without meaning, can be formed using all the letters ofthe word EQUATION, using each letter exactly once?
19. Since no letter is repeated in the word EQUATION.
The permutation of 8 letters taken all at a time
= 8P8
=
=
= 8! [since, 0! = 1]
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
26. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
26.The number of ways of selecting a team consisting of 3 boys from 5 boys and 3 girls from 4 girls is
5C3×4C3
= ×
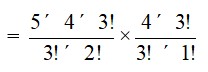
= ×
= 40
29. In how many ways can one select a cricket team of eleven from 17 players inwhich only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
29. We are given 17 players of which 5 players can bowl and 17 – 5 = 12 can bat. But we need to select a team of 11 in which there are exactly 4 bowlers.
Hence, the required number of ways
=5C4 (bowl) x 12C (11-4) (bat)
= ×
= 5 × 11 × 9 × 8
= 3960
30. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
30. We are given 5 black and 6 red balls of which 2 black and 3 red balls can be selected.
Thus the required number of ways
= 5C2×6C3
= ×
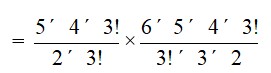
= 10 × 20
= 200
37. In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
37. Since out of 8 total questions at least 3 questions has to be attempted from each of part I and II containing 5 and 7 questions respectively we can have the choices.
(a) 3 questions from I and 5 questions from II selected in 5C3×7C5 ways.
(b) 4 questions from I and 4 questions from II selected in 5C4×7C4 ways.
(c) 5 questions from I and 3 questions from II selected in 5C5×7C3 ways.
Therefore, the required number of ways.
= (5C3×7C5) + (5C4×7C4) + (5C5×7C3)
= × + × + ×
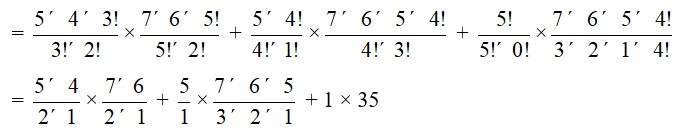
= (10 × 21) + (5 × 35) + 35
= 210 + 175 + 35
= 420
38. Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.
38. In a deck of 52 card there are four kings.
So, number of ways of selecting exactly one king is 4C1.
Now, after fixing one king card, we need to have the remaining 4 out of 5 cards to be a non-king i.e., only from the other 48 cards. So, number of ways of selecting is 48C4
Therefore, the required number of ways
= 4C1*48C4
40. From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?
40. In a class of 25 students, 10 students are to be selected for excursion. As 3 students decided that either all of them will join or none of them will join we have the options:
For the 3 students to be selected along with 7 other students from the remaining 25 – 3 = 22 students. This can be done in 3C3*22C7 ways.
For the 3 students to not be selected so that all 10 students will be from the remaining 25 – 3 = 22 students. This can be done in 3C0*22C10 ways.
Therefore, the required number of ways
= 3C3* 22C7 + 3C0*22C10
= 22C7 + 22C10
41. In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?
41. In the 13 letter word ASSASSINATION there are 3-A, 4-S, 2-I, 2-N, 1-T and 1-O.
Since all the S are to be occurred together we treat them i.e. (SSSS) as single object. This single object together with 13 – 4 = 9 remaining object will account for 10 objects having 3-A, 2-I, 2-N, 1-T and 1-O and can be rearranged in
= 10 * 9 * 8 * 7 * 6 * 5
= 151200
Class 11 Permutation and Combinations Exercise 6.2 Solutions
Permutation and Combinations Exercise 6.2 focuses on the concept of combinations, including selecting objects without considering their arrangement. exercise 6.2 focuses on the combination formula and its applications in different selection-based problems. Key topics covered include properties of combinations, the relation between permutations and combinations, and solving problems involving real-life scenarios such as forming teams, distributing objects, and selecting committees. Class 11 Permutation and Combinations Ex 6.2 solutions below;
Permutation and Combinations Ex 6.2 SolutionsQ1. Evaluate (i) 8 ! (ii) 4 ! – 3! |
| A.1. We know that, n! = n(n – 1)(n – 2)…….. i. 8! 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320 ii. 4! – 3! = (1 × 2 × 3 × 4) – (1 × 2 × 3) = 24 – 6 = 18 |
| Q2. Is 3 ! + 4 ! = 7 ! ? |
| A.2. L.H.S = 3! + 4! = (1 × 2 × 3) + (1 × 2 × 3 × 4) = 6 + 24 = 30 R.H.S = 7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040 As, L.H.S ≠ R.H.S 3! + 4! ≠ 7! |
| Q3.Compute |
| A.3. = = 4 × 7 = 28 |
| Q4.If , find x |
| A.4.We have, + = => + = => 1 + = => = =>x = 8 × 8 =>x = 64 |
| Q5.Evaluate when n = 6, r = 2(ii)n = 9, r = 5. |
| A.5.i.n = 6, r = 2
= = = 30 ii.n = 9, r = 5
= = = 9 × 8 × 7 × 6 × 5 = 15,120 |
Class 11 Permutation and Combinations Exercise 6.3 Solutions
Permutations and Combinations Class 11 Math Ex 6.3 focuses on the practical applications of permutations and combinations in different counting problems. This exercise 6.3 covers important topics such as arrangements of distinct and identical objects, selection under constraints, and real-life applications of counting principles. Students will find the solution to the Permutations and Combinations exercise 6.3 below.
Permutations and Combinations Exercise 6.3 SolutionsQ1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated? |
| A.1. The permutation of 9 different digits taken 4 at a time is given by 9P3 = = = = 9 × 8 × 7 = 504 |
| Q2. How many 4-digit numbers are there with no digit repeated? |
| A.2. For every four-digit number we have to count the permutation of 10 digits namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 taken 4 at a time i.e. 10P4 = = = 10 × 9 × 8 × 7 = 5040 However, these permutation will include those where 0 is at 1000’s place. So, fixing 0 at 1000’s place and rearranging the remaining 9 digits taking 3 at a time. i.e. 9P3= = = = 9 × 8 × 7 = 504 Therefore, The required number = 10P4 – 9P3 = 5040 – 504 = 4536 ways |
| Q3. How many 3-digit even numbers can be made using the digits1, 2, 3, 4, 6, 7, if no digit is repeated? |
| A.3. The permutation of having even number at the last digit from the given 6 different digits namely 1, 2, 3, 4, 5, 6 to form a 3-digit number is 3P1= = = = 3 After taking one of the even number as last digit we can rearrange the remaining 5 digits taking 2 at a time. i.e. 5P2 = = = = 5 × 4 = 20 Therefore, The required number = 20 × 3 = 60 |
| Q4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4,5 if no digit is repeated. How many of these will be even? |
| A.4. The permutation of 5 different digits namely 1, 2, 3, 4, 5 taken 4 at a time is 5P4 = = = 5 × 4 × 3 × 2 × 1 = 120 The permutation of having 2 or 4 at ones place is 2P1 = = = 1 × 2 = 2 After fixing one of the even number at last digit we can rearrange the remaining four digits taking 3 at a time. i.e. 4P3 = = = 4 × 3 × 2 × 1 = 24 Therefore, total permutation of 4 digit even number using 1, 2, 3, 4, 5 = 24 × 2 = 48 |
| Q5. From a committee of 8 persons, in how many ways can we choose a chairmanand a vice chairman assuming one person can not hold more than one position? |
| A.5.The permutation of 8 persons taken 2 positions at a time is 8P2 = = = 8 × 7 = 56 |
Q6. Find n if 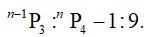 |
|
=> ÷ = => × = => = Therefore, n = 9 |
| Q7. Find r if |
|
=> = 2 => = => = => = 2 × 6 |
| Q8. How many words, with or without meaning, can be formed using all the letters ofthe word EQUATION, using each letter exactly once? |
| A.8. Since no letter is repeated in the word EQUATION. The permutation of 8 letters taken all at a time = 8P8 = = = 8! [since, 0! = 1] = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40320 |
| Q9. How many words, with or without meaning can be made from the letters of theword MONDAY, assuming that no letter is repeated, if. 4 letters are used at a time, all letters are used at a time, all letters are used but first letter is a vowel? |
| A.9. i.The permutation of 6 letters in MONDAY taken 4 at a time without repetition is 6P4 = = = 360 ii.The permutation of 6 letters in MONDAY when all letters are taken at a time is 6P6 = = = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720 iii.The permutation of having one of the two vowels (O, A) as first letter from the word MONDAY when all letters are taken at a time is 2P1 = = 2 After fixing one of the vowel as first letter we can rearrange the remaining 5 letters taking 5 at a time 5P5 = = = 5! = 5 × 4 × 3 × 2 × 1 = 120 Therefore, total permutation when all letters are used but first letter is vowel from the word MONDAY = 2 × 120 = 240 |
| Q10. In how many of the distinct permutations of the letters in MISSISSIPPI do thefour I’s not come together? |
| A.10. There are 11 letters of which M appears 1 time, I appears 4 times, S appears 4 times and P appears 2 times. The required number of arrangements = = = 11 × 10 × 9 × 5 = 34650 When the four I occurs together we treat them as single object IIII. This single object together with 7 remaining object will account for 8 object which have 1-M. 2-P and 4-S. So, required number of permutation = = = 840 Therefore, total no. of permutation in which 4-I’s do not come together = 34650 – 840 = 33810 |
| Q11. In how many ways can the letters of the word PERMUTATIONS be arranged if the words start with P and end with S, vowels are all together, there are always 4 letters between P and S? |
| A.11. There are 12 letters in which T appears 2 times and rest are all different. i.When P and S are fixed as first and last letter we can arrange the remaining 10 letter taking all at a time. i.e. Number of permutation = = = 18,14,400 ii.We take the 5 vowels (E,U,A,I,O) as one single object. This single object with the remaining 7 object are treated as 8 object which have 2 – T’s. So, number of permutations in which the vowels come together = permutation of 8 object x permutation within the vowels = × 5! = × 5 × 4 × 3 × 2 × 1 = 20160 × 120 = 2419200 iii.In order to have 4 letters between P and S, (P, S) should have the possible sets of places (1, 6), (2, 7), (3, 8), (4, 9), (5, 10), (6, 11) and (7, 12) similarly (S, P) should have the same possible sets of places. So, total number of possible positions fixed for P and S = 14 After fixing P and S we can rearrange the remaining 10 places with the remaining 10 letters of which 2 are T’s. So, required permutation = = = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 = 18,14,400 Therefore, total permutation for which there are always 4 letters between P and S = 14 × 18,14,400 = 2,54,01,600 |
Class 11 Permutation and Combinations Exercise 6.4 Solutions
Class 11 Permutation and Combinations Miscellaneous Exercise Solutions
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
- Relations and Functions
- Sets
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test