
Motion is everywhere in the universe, whether a person walks, runs, or when automobiles and planes carry people, and so on. In Class 11 Motion in a Straight Line, we will learn how to describe the motion, which is a change in the position of an object with respect to time. The chapter covers the velocity and acceleration concepts. Moreover, about the rectilinear motion and Kinematics.
The following are a few of the key topics covered in the Motion in a Straight Line Class 11:
- Relative Velocity
- Acceleration
- Kinematic Equations for Uniformly Accelerated Motion
- Instantaneous velocity and speed
To enhance their understanding of the NCERT Class 11 Physics, students should explore here. They will get important topics and free PDFs.
- Class 11 Physics Motion in a Straight Line: Key Topics, Weightage
- NCERT Solutions for Class XI Physics Motion in a Straight Line PDF Download
- Motion in a Straight Line Solutions
Class 11 Physics Motion in a Straight Line: Key Topics, Weightage
NCERT Solutions Motion in a Straight Line Class 11 explores the concepts and formulas related to motion. It is a crucial chapter for the JEE Main and NEET exams. The topics on which the students should focus are - displacement, acceleration, velocity, and equations of motion. See the table below for the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 2.1 | Introduction |
| 2.2 | Instantaneous Velocity and Speed |
| 2.3 | Acceleration |
| 2.4 | Kinematic Equations for Uniformly Accelerated Motion |
Motion in a Straight Line Class 11 Weightage in NEET and JEE Main Exams
| Exams | Number of Questions | Weightage |
|---|---|---|
| NEET | 1-2 questions | 4-5% |
| JEE Main | 1-2 questions | 4-8% |
NCERT Solutions for Class XI Physics Motion in a Straight Line PDF Download
Motion in a Straight Line Class 11 PDF explains the concepts of motion, path length, displacement, average velocity, instantaneous velocity, acceleration, and related topics. Practicing it helps students boost their exam preparation. They become more confident in solving complex problems. Students must download the free PDF from the link given below:
Download Here: NCERT Solutions for Class XI Physics Motion in a Straight Line PDF
Motion in a Straight Line Solutions
| Q.3.1 In which of the following examples of motion, can the body be considered approximately a point object: (a) A railway carriage moving without jerks between two stations
(b) A monkey sitting on top of a man cycling smoothly on a circular track
(c) A spinning cricket ball that turns sharply on hitting the ground
(d) A tumbling beaker that has slipped off the edge of a table |
| Ans.3.1 (a) The length of the carriage is very small compared to the distance between 2 stations. Hence the carriage can be considered a point object
(b) The size of the monkey is very small compared to the length of the track, hence it can be considered as a point object
(c) The size of the cricket ball is comparable considering the distance between wickets, hence it cannot be considered as a point object
(d) The height of the beaker is comparable considering the height, from which it has fallen. Hence it cannot be considered as point object |
| Q.3.2 The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. 3.19. Choose the correct entries in the brackets below; (a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice) |
| Ans.3.2 (a) A lives closer to the school than B ( OP
(b) A starts earlier than B from school. From the graph, A starts from O at time 0 whereas B starts after some finite value t
(c) B walks faster than as the slope for B is steeper than A
(d) Both B and A reaches home at the same time
(e) At the intersection of the two lines, it is evident that B overtakes A once |
| Q 3.3 A woman starts from her home at 9.00 am, walks with a speed of 5 km h–1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h–1. Choose suitable scales and plot the xt graph of her motion.
|
| Ans.3.3 Office distance = 2.5 km Walking speed = 5 kph Time taken to reach office = 5/2.5 = 0.5 h OA is the path to reach office AB is the duration of office stay Auto speed = 25 kph Time taken by auto = 2.5/25 h = 6 minutes BC is the path for returning |
| Q.3.4 A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1 s. Plot the xt graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start. |
| Ans.3.4 The time taken for each step is 1s, he covers 5 m in 5 secs and goes backward by 3 m in 3 secs. So in 8 s he covers 2 m. To cover 13m distance he needs to complete 8 m (13-5). To cover 8m, he will require 8 × 4 = 32 s. To fall in a pit, he needs to move anther 5m in 5s. So total time taken = 32 +5 = 37 s |
Commonly asked questions
3.12 A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Given data:
Initial height, h = 90 m
Acceleration due to gravity, g = 9.8 ms2
Speed lost at each collision = 1/10 of its speed
time interval to be considered: 0 to 12 secs.
Step 1: Time to fall from 90 m
h = ½ gt2 ⇒ 90 = 21 × 9.8 × t2 ⇒ t2 = 9.8180 ≈ 18.37 ⇒ t ≈ 4.29 seconds
Step 2: Speed before first impact
v = gt = 9.8 × 4.29 ≈ 42 m/s
After hitting the floor with 42 m/s, ball rebound with;
vrebound = 0.9×42 = 37.8m/s
Step 3:
Max height after rebound:
Use:
t = g / v = 37.8 / 9.8 ≈ 3.86s
Again, the ball fall back in time 3.86 s, hitting the ground with
v = g × 3.86 ≈ 37.8 m/s
Rebound = 0.9×37.8=34.0 m/s
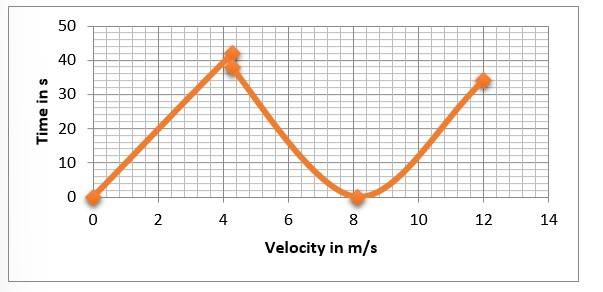
3.14 A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h–1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h–1.
What is the
(a) Magnitude of average velocity, and
(b) Average speed of the man over the interval of time
(i) 0 to 30 min,
(ii) 0 to 50 min,
(iii) 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]
3.14
The distance from home to market = 2.5 km = 2500 m
The speed of the walking while going = 5 kmph = 1.388 m/s
The speed of walking back from market to home = 7.5 kmph = 2.083 m/s
(a) Magnitude of the average velocity = Displacement / time = 0, since the total displacement is zero.
(b)
i. Time taken to reach the market = distance / onward speed = 2500/1.388 = 1801 s = 30 minutes. So the average speed over 0 – 30 min is 5 kmph
ii. Time taken to reach back home = 2500 / 2.083 = 20 minutes. So the average speed = total distance covered / total time taken = (2500 +2500)/ (30 +20) m/min = 100 m/min = 6 kmph
iii. Average speed over the interval of time 0 to 40 mins = Distance covered / time taken = 2500 + (2.083 * 10 * 600) / (40 * 60) = 1.5624 m/s = 5.62 kmph
3.16 Look at the graphs (a) to (d) (Fig. 3.20) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.
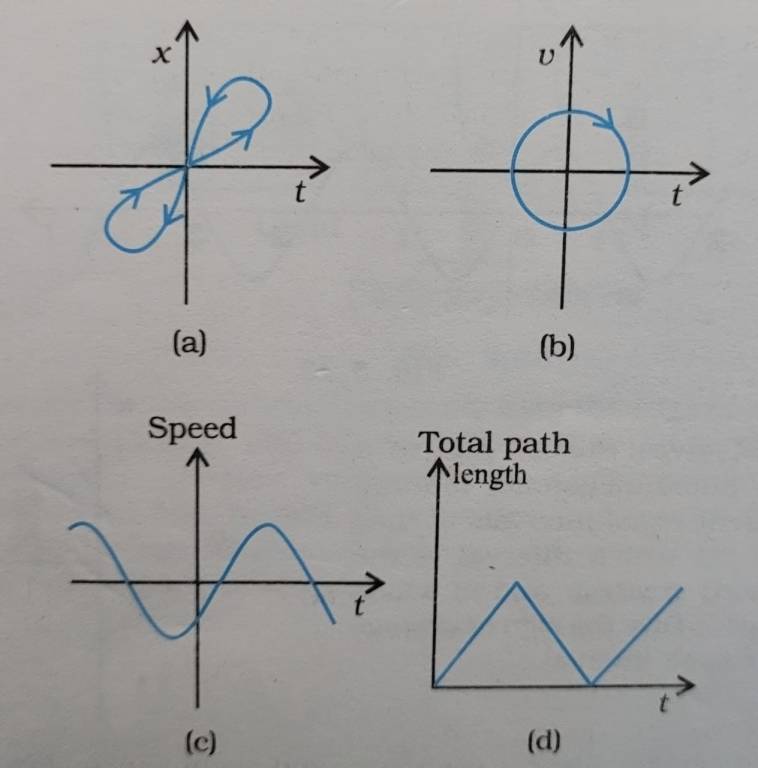
3.16
(a) Figure (a) shows two positions at the same time, which is not possible for a one-dimensional motion
(b) A particle cannot have velocity in two directions at the same time in one-dimensional motion
(c) The graph shows negative speed, which is not possible because speed is always positive
(d) Total path length decreases, which is not possible for a one – dimensional motion
3.18 A police van moving on a highway with a speed of 30 km h–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h–1. If the muzzle speed of the bullet is 150 m s–1, with what speed does the bullet hit the thief’s car?
(Note: Obtain that speed which is relevant for damaging the thief’s car).
3.18 Speed of the police van = 30 kmph = 8.33 m/s
Speed of the thief's car = 192 kmph = 53.33 m/s
The muzzle speed of the bullet = 150 m/s
Speed of the bullet = speed of the police van + muzzle speed of the bullet = 8.33 + 150m/s = 158.33 m/s
The relative velocity of the bullet = speed of the bullet – speed of the thief's car = 158.33 – 53.33 m/s = 105 m/s
3.6 A car moving along a straight highway with speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
3.6 The speed of the car = 126 kmph = (126 * 1000/3600) m/sec = 35 m/s
From the relation V2 = U2 + 2fs, where Final velocity V = 0, U = 35 m/s, s = 200m, we get retardation, f = -U2/2s= 3.06 m2/s
From the relation V = U – ft, we get t = U/f = 35/3.06 = 11.42 s.
3.21 Figure 3.24 gives the x-t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest, and in which is it the least? Give the sign of average velocity for each interval.
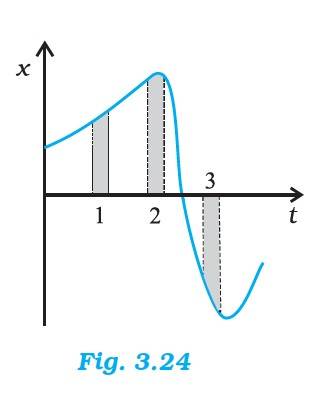
3.21 The average speed in Interval 3 is the greatest and in Interval 2 is the least.
The average velocity is +ve in Interval 1 & 2 and –ve in Interval 3.
3.22 Figure 3.25 gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?
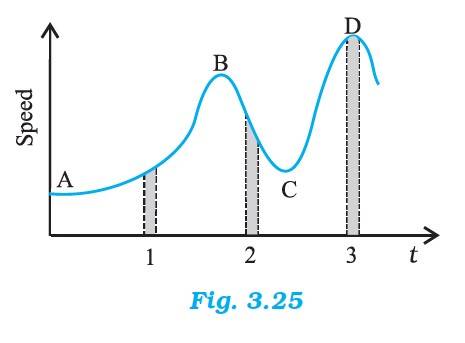
3.22 The change in the speed with time is maximum in interval 2. Therefore, the average acceleration is the greatest in magnitude in interval 2
The average speed is maximum in interval 3
The sign of velocity is positive in intervals 1,2 and 3
Acceleration depends on the slope. The acceleration is positive in interval 1 and 3, as the slope is positive. The acceleration is negative in interval 2, as the slope is negative
Acceleration at A, B, C and D is zero since the slope is parallel to the time axis at these instants
3.13 Explain clearly, with examples, the distinction between:
(a) Magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval
(b) Magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]
Show in both (a) and (b) that the second quantity is either greater than or equal to the first
When is the equality sign true? [For simplicity, consider one-dimensional motion only]
3.13
(a) Let us take the example of football world cup 2022. During Argentina match, Di Mario (A) passed the ball to Messi (B). Messi instantly passed the ball to Di Mario. Now the magnitude of displacement of the ball is 0 as the ball returns to Di Mario at the initial position. But the total length covered by the ball is AB + BA = 2AB. Hence total length covered by the particle (the ball) is more than the magnitude.
(b) If t is the time taken to cover the entire distance, the magnitude of the average velocity of the ball over time interval t = Magnitude of displacement / t = 0 / t = 0
The average speed of the ball = Total length of the path / time interval = 2AB / t
Thus the second quantity is greater than the first.
If the ball moves only in one direction from A to B, both the quantities are equal (considering one-dimensional motion)
3.10 A player throws a ball upwards with an initial speed of 29.4 m s–1.
(a) What is the direction of acceleration during the upward motion of the ball?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion
(d) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance)
3.10
(a) The direction of the acceleration is downward during the upward motion of the ball because the acceleration is due to gravity. Gravity always pulls the object toward the centre of the earth.
(b) Velocity: At the peak the velocity is zero because the ball momentarily stops before falling downwards.
Acceleration: g = 9.8 ms–2
(c) If we consider the highest point x = 0 m, t= 0 s,
During upward motion of the ball before it reaches the maximum height, x = +ve, velocity = -ve, acceleration = +ve. During downward motion, x = +ve, velocity = +ve, acceleration = +ve
(d) At the highest point, final velocity v = 0, initial velocity = 29.4 m/s, acceleration = 9.8m/s2
From the equation v2-u2 = 2gs, we get s = (29.4)2/2 * 9.8 = 44.1 m. From v –u = gt we get t = 29.4/9.8 s = 3 s. So the total time taken by the ball to reach player's hand = 3 * 2s = 6 s
3.19 Suggest a suitable physical situation for each of the following graphs (Fig 3.22):

(a) This graph is a Displacement-Time Graph (x- t) that shows the displacement increasing From A to B, and decreasing From B to C. The graph may represent a carom board where the striker hits the edge, rebounds with reduced speed, then moves in the opposite direction, hits the opposite wall and stops.
(b) This graph is a Velocity-Time Graph (v- t) that shows Sudden spikes and drops in velocity. There is a rapid change in velocity. This graph may represent a ball that falls on the ground from a certain height and rebounds with a reduced speed
(c) This graph is an Acceleration -Time Graph (a- t) that shows an instantaneous spike in acceleration. The graph looks like of a baseball, thrown on to a batter, moves with a uniform speed and then hit by the bat for a very short time interval.
3.17 Figure 3.21 shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t >0? If not, suggest a suitable physical context for this graph.
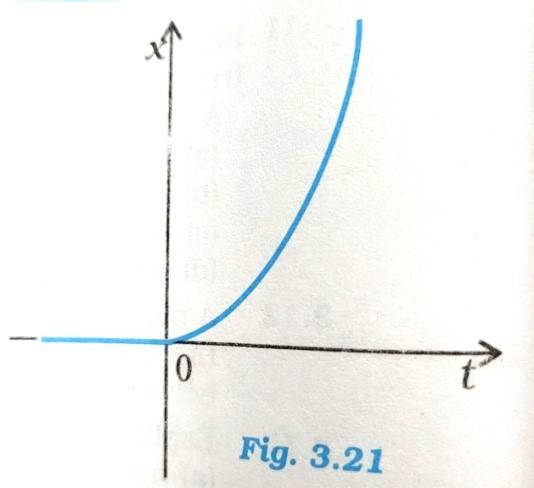
3.17 For t<0, we cannot say that the particle moved in a straight line and for t>0 on a parabolic path as the x-t graph does not indicate. Instead, this x-t graph denotes a particle is dropped from a height at t=0
3.27 The speed-time graph of a particle moving along a fixed direction is shown in Fig. 3.28. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s (b) t = 2 s to 6 s.

3.27
(a) Distance travelled by the particle between t = 0 s and t = 10 s is the area of the triangle = (1/2) x base x height = (1/2) x 10 x 12 = 60 m
The average speed of the particle is 60/10 m/s = 6 m/s
(b) Distance travelled by the particle between t = 2 s and t = 6 s
Let S1 be the distance travelled by the particle in time 2 to 5 s and S2 be the distance travelled between 5 to 6s.
For the motion from 0 to 5 sec, u = 0, t = 5, v = 12 m/s
From the equation v = u + at we get a = (v-u)/t = 12/5 = 2.4 m/s2
Distance covered from 2 to 5 sec, S1 = distance covered in 5 s – distance covered in 2 s
From the equation s = ut + at2 we get,
= (1/2) * 2.4 * 25 – (1/2) * 2.4 * 4 = 30 – 4.8 = 25.2 m
For the motion from 5 sec to 10 sec, u = 12 m/s and a = -2.4 m/s2
and t = 5 sec to t = 6 sec means n = 1 for this motion
Distance covered in the 6th sec is S2 = u + (1/2) a (2n-1) = 12 + (1/2) (-2.4) (2 * 1-1) = 10.8 m
Therefore the total distance covered from t = 2 to 6 s = 25.2 + 10.8 m = 36 m
3.7 Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m s–2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
3.7 The uniform speed of A and B = 72 kmph = 20 m/s
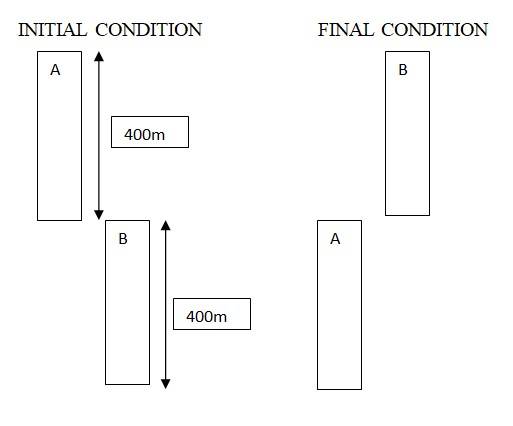
The acceleration f = 1 m/s2, time t = 50 s
Distance covered by train B = ut + 0.5 * ft2 = 20 * 50 + 0.5 * 1 * 50 2 = 2250 m
Distance covered by train A in the same period = ut = 50 * 20 = 1000 m
So the initial distance train A and train B was = 2250 – 1000 = 450 m
3.11 Read each statement below carefully and state with reasons and examples, if it is true or false;
A particle in one-dimensional motion
(a) With zero speed at an instant may have non-zero acceleration at that instant
(b) With zero speed may have non-zero velocity
(c) With constant speed must have zero acceleration
(d) With positive value of acceleration must be speeding up
3.11
(a) True – zero speed may have a non zero instantaneous non-zero acceleration
(b) False – zero speed will always make zero velocity
(c) True – constant speed will have zero acceleration
(d) False – If the positive value of acceleration is in the direction of its motion then it can speed up
3.15 In Exercises 3.13 and 3.14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
3.15 Instantaneous speed and velocity are applicable for a small interval of time because the magnitude of the displacement is effectively equal to the distance travelled by the particle.
3.5 A jet airplane travelling at the speed of 500 km h–1 ejects its products of combustion at the speed of 1500 km h–1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?
3.5 The speed of the jet plane, Vj = 500 kmph. If the speed of the product of combustion is Vpc, then V pc = Vpc-Vj = -1500 kmph (relative to the jet plane)
Speed of the combustion product relative to the observer on the ground,
Vpc = -1500 + Vj = -1500+500 = -1000 kmph
3.20 Figure 3.23 gives the x-t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
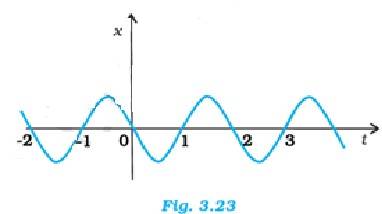
3.20 In simple harmonic motion, the acceleration is expressed as a = - 2x, where is the angular frequency.
(a) At t = 0.3 s, position x is negative, velocity v is negative and acceleration a ( from above equation) will be positive
(b) At t = 1.2 s, position x is positive, velocity is positive, acceleration a will be negative
(c) At t = -1.2 s, position x is negative, velocity is positive and acceleration will be positive.
3.28 The velocity-time graph of a particle in one-dimensional motion is shown in Fig 3.29 :
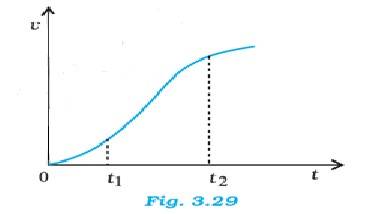
Which of the following formulae are correct for describing the motion of the particle
over the time-interval t1 to t2:
(a) x(t2 ) = x(t1) + v (t1) (t2 – t1) +(½) a (t2 – t1)2
(b) v(t2 ) = v(t1) + a (t2 – t1)
(c) vaverage = (x(t2) – x(t1))/(t2 – t1)
(d) aaverage = (v(t2) – v(t1))/(t2 – t1)
(e) x(t2 ) = x(t1) + vaverage (t2 – t1) + (½) aaverage (t2 – t1)2
(f) x(t2 ) – x(t1) = area under the v-t curve bounded by the t-axis and the dotted line
shown.
3.28 The graph has a non-uniform slope between the intervals t1 and t2 – the graph is not a straight line. The equations (a), (b), and (e) do not describe the motion of the particle. Only the relations (c), (d) and (f) are correct.
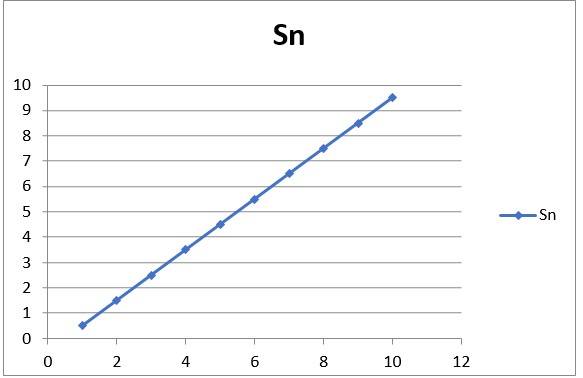
3.23 A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
3.23 The distance covered by the 3 wheeler on a straight line in the nth second can be expressed as:
Sn = u + a (2n-1)/2 …… (1),
Where
a = acceleration
u = initial velocity
n = time = 1,2,3, ……., n
Given, u = 0, a = 1m/s2, from equation (1) we get Sn = (2n-1)/2 ……. (2)
With various values of n, we get Sn
n Sn
1 0.5
2 1.5
3 2.5
4 3.5
5 4.5
6 5.5
7 6.5
8 7.5
9 8.5
10 9.5
3.4 A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1 s. Plot the xt graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
3.4
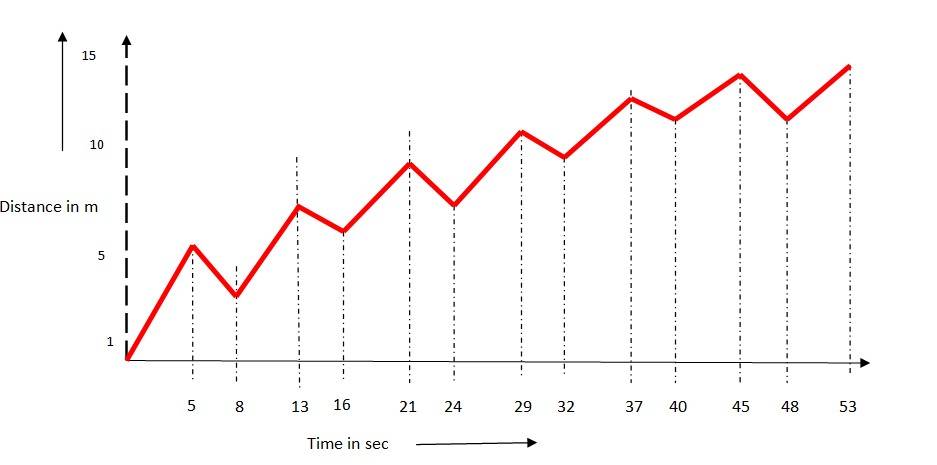
The time taken for each step is 1s, he covers 5 m in 5 secs and goes backward by 3 m in 3 secs.
So in 8 s he covers 2 m. To cover 13m distance he needs to complete 8 m (13-5). To cover 8m, he will require 8 * 4 = 32 s. To fall in a pit, he needs to move another 5m in 5s.
So total time taken = 32 +5 = 37 s
Let’s have a look at how we came to this answer.
We have to calculate how long it will take for the drunkard to fall into a pit located 13 metres from his starting point.
In each cycle of movement, the drunkard takes 5 steps forward and 3 steps backward. We calculate the net displacement per cycle.
Time for one cycle = 5 seconds (forward) + 3 seconds (backward) = 8 seconds.
Net displacement in one cycle = 5 meters (forward) - 3 meters (backward) = 2 meters.
Reaching the pit: The pit is 13 metres away. We can determine the time taken by analysing his position after each cycle.
After 1 cycle (8 s): Position = 2 m
After 2 cycles (16 s): Position = 4 m
After 3 cycles (24 s): Position = 6 m
After 4 cycles (32 s): Position = 8 m
At the 32-second mark, the drunkard is at the 8-metre position. This we get to know when learning about instantaneous velocity.
In his next set of forward steps, he will cover 5 metres in 5 seconds. This means he will reach the 13-metre mark and fall into the pit.
Total time calculation: The total time is the time taken to reach the 8-metre mark plus the time to take the final 5 steps.
Total time = 32 seconds + 5 seconds = 37 seconds.
Practice more NCERT Solutions for Motion in a Straight Line chapter.
3.9 Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h–1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
3.9 Cycling speed = 20 kmph
Let as assume speed of the bus is
The relative velocity of the buses in the direction of motion of the cyclist = -
Buses go past him every 18 mins = 18/60h = 0.3h
Distance covered = ( ) × 0.3
Since the buses leave every T minutes, ( ) × 0.3 = × (T/60) ……(1)
The relative velocity of the buses in the opposite direction of the cyclist = +
Buses go past him in the opposite direction = every 6 m = 6/60 h
Distance covered = ( + ) × 1/10
Since the buses leave every T minute, we get ( + ) × 1/10 = × T/60 …….(2)
From equations (1) & (2), we get
( + ) / 10 = ( ) × 0.3
+ = 3( - 3 )
2 = 4 , = 2 So = 2 × 20 = 40 kmph
From the equation (1), we get
(40-20) × 0.3 = 40 × T/60, T = 9 min
3.25 On a long horizontally moving belt (Fig. 3.26), a child runs to and fro with a speed 9 km h –1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h–1. For an observer on a stationary platform outside, what is the
(a) Speed of the child running in the direction of motion of the belt?
(b) Speed of the child running opposite to the direction of motion of the belt?
(c) Time taken by the child in (a) and (b)?
Which of the answers alter if motion is viewed by one of the parents?
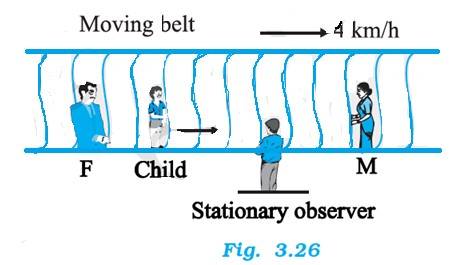
Speed of belt = 4 km/h
(a) When the boy runs in the direction of motion of the belt, then the speed of the child observed by the stationary observer = 9 + 4 = 13 km/h
(b) When the boy runs in the opposite direction of motion of the belt, then the speed of the child observed by the stationary observer = 9-4 = 5 km/h
(c) Distance between the parents = 50 m = 0.05km
Speed of the boy, as observed by both parents = 9 km/h.
Time required by the boy to move to any parent = 0.05 / 9 h = 20s
Q.3.1 In which of the following examples of motion, can the body be considered approximately a point object:
(a) A railway carriage moving without jerks between two stations
(b) A monkey sitting on top of a man cycling smoothly on a circular track
(c) A spinning cricket ball that turns sharply on hitting the ground
(d) A tumbling beaker that has slipped off the edge of a table
This question belongs to the Motion in a straight line chapter that we will be solving this with explanation.
(a) A railway carriage moving without jerks between two stations
Whenever a railway carriage moves between two stations smoothly without jerks, it is considered as a point object. This is due to the fact that distance between the two stations is larger as compared to the size of carriage. However, we are interested in the overall motion instead of the movement of specific parts of carriage.
(b) A monkey sitting on top of a man cycling smoothly on a circular track
Here, both monkey as well as the cyclist are considered as a single point object if we analyze their motion on the circular track. The radius of the circular path is much larger as compared to the size of the monkey and cyclist. This makes the point object approximation valid for studying overall motion.
There are more complex and other important questions in the NCERT excercise of Motion in a Straight Line that you can check out for verifying if you are answering questions correctly.
(c) A spinning cricket ball that turns sharply on hitting the ground
A spinning cricket ball that turns sharply on hitting the ground is not a point object. The spin and sharp turn are highly influenced by the size, shape and rotation of the ball. This affects the trajectory of the ball and its interaction with the ground.
(d) A tumbling beaker that has slipped off the edge of a table
A tumbling beaker which has slipped off a table is not a point object since it involves rotation and changes in the orientation. These depend on the shape and size of beaker.
Students must go through those solutions if they are currently studying in class 12th and soon they have to take the 12th CBSE board exam.
3.8 On a two lane road, car A is travelling with a speed of 36 km h–1. Two cars B and C approach car A in opposite directions with a speed of 54 km h–1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?
3.8

Speed of car A, Va = 36 kmph = 10m/s
Speed of car B, Vb = 54 kmph = 15 m/s
Speed of car C, Vc = -54 kmph = -15 m/s
Relative speed of A, w.r.t. C = Va – (-Vb) = 10 +15 = 25 m/s
Relative speed of B, w.r.t. A = Vb-Va = 15-10 = 5 m/s
Distance between AB & AC = 1 km = 1000m
Time taken by the car C to cover the distance AC, from s = ut
We get t = 1000/25 = 40s
To avoid collision with C, the minimum acceleration the vehicle B must have, from the relation, s = ut + (1/2) ft2
We get 1000 = 5 * 40 + (1/2) f * 402 f = 1 m/s2
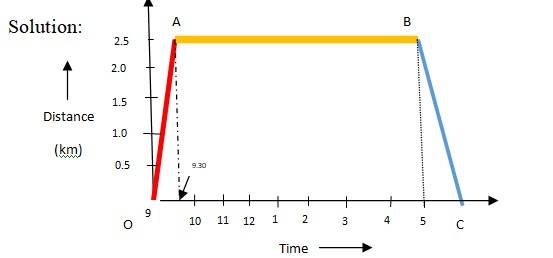
3.3 A woman starts from her home at 9.00 am, walks with a speed of 5 km h–1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h–1. Choose suitable scales and plot the xt graph of her motion.
3.3 Office distance = 2.5 km
Walking speed = 5 kph
Time taken to reach office = 5/2.5 = 0.5 h
OA is the path to reach office
AB is the duration of office stay
Auto speed = 25 kph
Time taken by auto = 2.5/25 h = 6 minutes
BC is the path for returning
On the position-time graph, this is a straight line sloping downwards. It starts at the point representing 5:00 PM and 2.5 km, and ends at 5:06 PM at 0 km. It tells us that the woman has arrived home.
The slope of this line represents instantaneous velocity. Because the return trip is by the auto at a much higher speed (25 km/h), the slope of line BC is significantly steeper than the line for the outward journey. A steeper slope on a position-time graph denotes a higher speed.
Master such questions with our NCERT Solutions for Motion in a Straight Line.
3.2 The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. 3.19. Choose the correct entries in the brackets below;
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice)
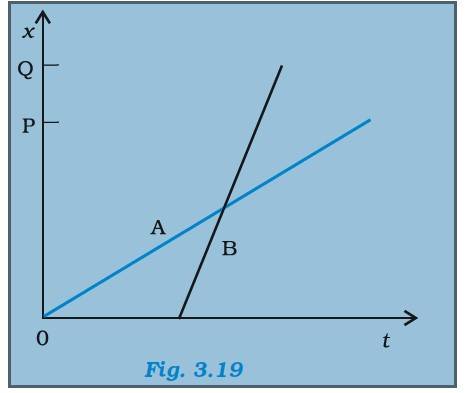
3.2
(a) A lives closer to the school than B ( OP
(b) A starts earlier than B from school. From the graph, A starts from O at time 0 whereas B starts after some finite value t
(c) B walks faster than as the slope for B is steeper than A
(d) Both B and A reaches home at the same time
(e) At the intersection of the two lines, it is evident that B overtakes A once
3.24 A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m s–1. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m s-1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
3.24 The initial velocity of the ball, u = 49m/s
First Case: When the ball returns to his hands, total displacement = 0
From the relation s = ut + 0.5at2, we get 0 = 49t + 0.5 (-9.81) t2
4.905 = 49t Hence t = 10s
Second Case:
As the lift started moving up with a speed of 5 m/s, the initial velocity of the ball = 49 + 5 m/s = 54 m/s
If t' is time for the ball to return to his hand, the displacement of the ball will be = 5t'
From the relation s = ut + 0.5 x at2, we get
5t' = 54t' + 0.5 * (-9.8) t'2
49t' = 4.9 t'2
t' = 10 s
3.26 Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m s–1 and 30 m s–1. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m s–2. Give the equations for the linear and curved parts of the plot.
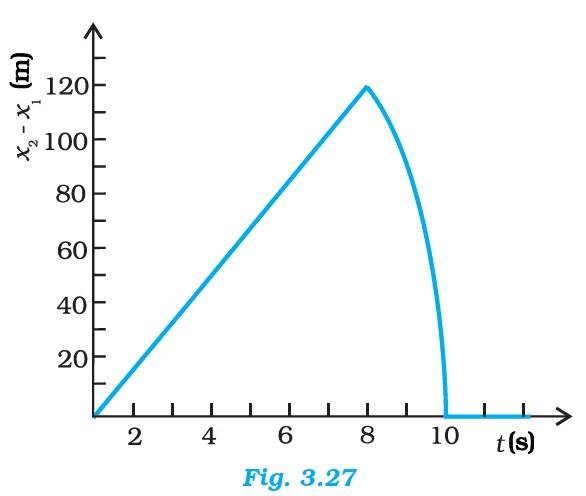
Initial velocity, u1 = 15m/s, acceleration, a = -g = -10 m/s
From the relation s1=s0+u1t+ (1/2)at2 where
s0 = cliff height, s1 = total height of the fall of the first stone, we get
s1 = 200 + 15t – 5t2 ………. (1)
When the stone hit the floor, s1 = 0, so the equation (1) becomes
0 = 200 +15t - 5t2 = t2 -3t – 40 = (t-8) (t+5) = 0
So t = 8s or -5s
Since the stone was thrown at t=0, so t cannot be –ve. Hence t = 8s
For the second stone,
Initial velocity, u1 = 30 m/s, acceleration, a = -g = -10 m/s
From the relation s2=s0+u1t+ (1/2)at2 where
s0 = cliff height, s2= total height of the fall of the second stone, we get
s2 = 200 + 30t – 5t2 ………. (2)
When the stone hit the floor, s2 = 0, so the equation (2) becomes
0 = 200 +30t - 5t2 = t2 -6t – 40 = (t-10) (t+4) = 0
So t = 10s or -4s
Since the stone was thrown at t=0, so t cannot be –ve. Hence t = 10s
Subtracting equation (1) from equation (2), we get
s2 – s1 = (200 + 30t – 5t2 ) – (200 + 15t – 5t2 ) = 15t ……. (3)
Equation (3) represents the linear trajectory of the two stones because to this linear relation between (s2 – s1) and t, the projection is straight line till 8s (from the graph)
The maximum distance between the two stones is at t = 8s. So
(s2 – s1) max = 15 x 8 = 120 m. This value has been depicted correctly in the graph.
After 8s, only the second stone is in motion (t for first stone has been found out to be 8s), the trajectory of second stone is obtained in equation (2), = 200 + 30t – 5t2 , which is a curved path.
Explore exams which ask questions on physics ncert solutions class 11th
Select your preferred stream
physics ncert solutions class 11th Exam
Student Forum
Other Similar chapters for you
- NCERT Physics 11th
- Physical World
- Units and Measurements
- Motion in a Straight Line
- Motion in a Plane
- Laws of Motion
- Work, Energy, and Power
- System of Particles and Rotational Motion
- Gravitation
- Mechanical Properties of Solids
- Mechanical Properties of Fluids
- Thermal Properties of Matter
- Thermodynamics
- Kinetic Theory
- Oscillations
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test
