When at the end of the Work, Energy, Power chapter, you will come across the topic of collision. It's an interesting phenomenon to decode.
Today we explore the collision definition in detail, with some basic to intermediate level explanations of its types and calculations so that you are confident with your exams - whether in school or your engineering entrances you are planning to prepare for.
So, follow this guide along with the Physics NCERT Solutions for Chapter 5.
- What is Collision?
- Types of Collision
- Process of Collision and Coefficient of Restitution
- Impulse-Momentum Theorem during Impact
- Coefficient of Restitution
- Head on Collision
- Special cases of head on elastic collision
- Oblique Collision
What is Collision?
Collision or Impact is the interaction between two bodies during a minimal duration in which they exert relatively large forces on each other. Interaction forces during an impact are created either due to direct contact, strong repulsive force fields, or some connecting links.
The duration of the interaction is short enough to permit us only to consider the states of motion just before and after the event, and not during the impact. The duration of an impact ranges from for impacts between elementary particles to millions of years for impacts between galaxies. The impacts we observe in our everyday life, such as those between two balls that last from to few seconds.
Let's look into some examples of collision to understand it better.
Direct collision: - When a rubber ball strikes a floor, it remains in contact with the floor for a very short time during which it changes its velocity. This is an example of a collision where physical contact takes place between the colliding bodies.
Indirect collision: - When an -particle passes by the nucleus of a gold atom in Rutherford's experiment, it gets deflected in a very short time. Deflection means a change in the direction of motion- a change in velocity. In this process, the particles do not touch each other.
Effects of collision, the momentum and kinetic energy of the interacting bodies change.
Interacting forces during collision are so large compared to other external forces acting on either of the bodies that the effects of the latter can be neglected. Then, forces involved in a collision are action-reaction pairs, i.e., the internal forces of the system and thus the total momentum remains conserved in any type of collision.
Understanding this concept of collision will be quite helpful for your JEE Mains.
Types of Collision
We can categorise different types of collisions based on the following criteria.
(a) On the basis of direction
On the basis of direction there are two types of collision.
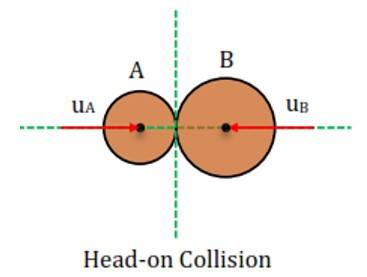
(i) Head-on Collision
A Collision in which the particles move along the same straight line before and after the collision is defined as Head-on Collision or One-dimensional Collision.
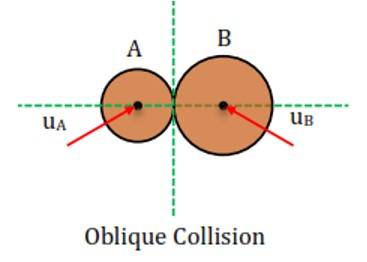
(ii) Oblique Collision
A Collision in which the particles move along the same plane at different angles before and after the collision is defined as an Oblique Collision or a Two-dimensional Collision.
(a) On the basis of kinetic energy: -
On the basis of kinetic energy, there are three types of collision.
(i) Elastic Collision
A Collision is said to be elastic if the total kinetic energy before and after the collision remains the same.
(ii) Inelastic Collision
A Collision is said to be Inelastic if the total kinetic energy before and after the collision does not remain same.
(iii) Perfectly Inelastic Collision
A Collision in which interacting particles get stuck together after the collision is called a Perfectly Inelastic Collision. In this type of collision, the loss of energy is maximum.
Process of Collision and Coefficient of Restitution
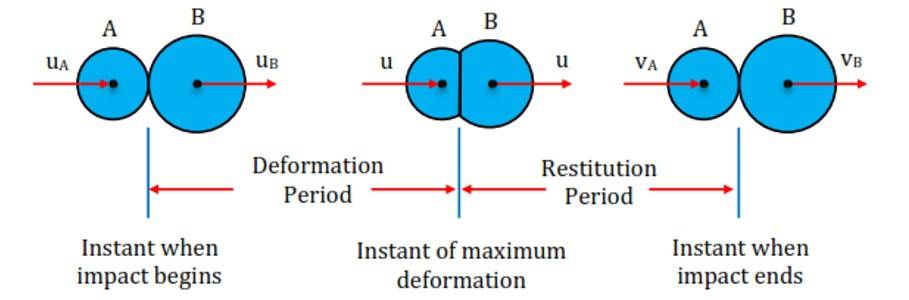
To understand mechanism of a collision, let us consider two balls and of masses and moving with velocities and in the same direction as shown. Velocity is larger than so that the ball hits the ball B. During the impact, both the bodies push each other and first they get deformed till the deformation reaches a maximum value and then they try to regain their original shapes due to elastic behaviour of the materials the balls formed of.
Deformation period: - The time interval during which deformation takes place.
During the period of deformation, due to push applied by the balls on each other during period of deformation speed of ball A decreases and that of ball B increases and at the end of the deformation period, when the deformation is maximum both the balls move with the same velocity say it is .
Thereafter, the balls will either move together with this velocity or follow the period of restitution.
Restitution period: - The time interval in which the bodies try to regain their original shapes.
During the period of restitution due to push applied by the balls on each other, speed of the ball A decreases further and that of ball B increases further till they separate from each other.
Let us denote the velocities of the balls
and
after the impact by
and
respectively.
Impulse-Momentum Theorem during Impact
(a) Deformation period
Applying impulse-momentum principle on ball A during deformation period
…..(i)
Applying impulse-momentum principle on ball during deformation period

….(ii)
(b) Restitution period
Applying impulse-momentum principle on ball A during restitution period
…..(iii)
Applying impulse-momentum principle on ball during restitution period
……(iv)
Conservation of Momentum during impact
From equations, (i) and (ii) we have
From equations, (iii) and (iv) we have
From equations, (v) and (vi) we obtain the following equation.
Hence, Total Initial Momentum = Total Final Momentum
The above equation elucidates the principle of conservation of momentum.
Coefficient of Restitution
Usually the force D applied by the bodies A and B on each other during the period of deformation differs from the force R applied by the bodies on each other during the period of restitution.
Therefore, it is not necessary that the magnitude of impulse due to deformation equals to that of impulse due to restitution.
The ratio of magnitudes of impulse of restitution to that of deformation is called the coefficient of restitution and is denoted by e.
Coefficient of restitution depends on various factors as elastic properties of materials forming the bodies, velocities of the contact points before impact, state of rotation of the bodies and temperature of the bodies. In general, its value ranges from zero to one but in collisions where additional kinetic energy is generated, its value may exceed one.
Depending on the values of coefficient of restitution, two particular cases are of special interest.
Perfectly Plastic or Inelastic Impact For these impacts e , and bodies undergoing impact stick to each other after the impact.
Perfectly Elastic Impact For these impacts e .
Strategy to solve problems of head-on impact:
Write the momentum conservation equation;
Write the equation involving coefficient of restitution
Head on Collision
If velocity vectors of the colliding bodies are directed along the line of impact, the impact is called a direct or Head-on impact.
Head on Elastic Collision
The head on elastic collision is one in which the colliding bodies move along the same straight-line path before and after the collision.
Assuming initial direction of motion to be positive and (so that collision may take place) and applying law of conservation of linear momentum
…..(i)
For elastic collision, kinetic energy before collision must be equal to kinetic energy after collision, i.e.,
…..(ii)
Dividing equation (ii) by (i)
…..(iii)
In 1-D elastic collision 'velocity of approach' before collision is equal to the 'velocity of separation after collision, no matter what the masses of the colliding particles are.
This law is called Newton's law for elastic collision.
Thus, value of coefficient of restitution for elastic collision;
If we multiply equation (iii) by
and subtract it from (i)
…..(iv)
Similarly, multiplying equation (iii) by and adding it to equation (i)
…..(v)
Special cases of head on elastic collision
Case-1: If the two bodies are of equal masses: then and
Thus, if two bodies of equal masses undergo elastic collision in one dimension, then the bodies exchange their velocities after the collision.
Case-2: If the two bodies are of equal masses and second body is at rest.
and initial velocity of second body
When body collides against body of equal mass at rest, then body comes to rest and body moves on with the velocity of body . In this case transfer of energy is hundred percent e.g. Billiard's Ball, Nuclear moderation.
Case-3: If the mass of one body is negligible as compared to the other.
If
and
then
When a heavy body A collides against a light body B at rest, then body A should keep on moving with same velocity whereas body
moves with velocity double that of
.
If
and
then
When a light body A collides against a heavy body B at rest, the body A starts moving with same speed just in opposite direction while the body B practically remains at rest.
Head on Inelastic Collision
By definition of coefficient of restitution
Loss in Kinetic Energy of particles
Value of coefficient of restitution for Inelastic collision is
Head on Perfectly Inelastic Collision
Where final velocity
Loss in Kinetic Energy of particles
Value of coefficient of restitution for Perfectly Inelastic collision e
.
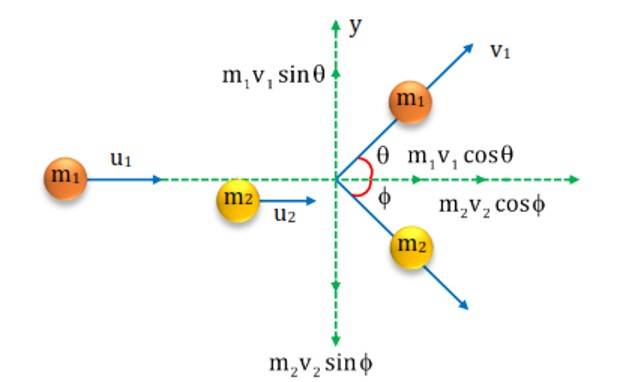
Oblique Collision
Physics Work, Energy and Power Exam
Student Forum
Other Topics under this Chapter
- Disadvantages of Biogas
- Concept of Potential Energy
- Power
- Potential Energy of Spring
- Conservation of Mechanical Energy
- Kinetic Energy
- Collision
- Work
- Types of Potential Energy
- Derivation of Work Energy Theorem
- Derivative of Potential Energy
- Elastic Potential Energy
- Thermal Power Plant Diagram
- Kinetic Energy and Potential Energy
- Derivation of Kinetic Energy
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test