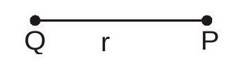Potential due to a point charge is where the concept of electrostatic potential starts becoming more interesting. Because it shows how the influence of an electric charge changes with distance from the charge itself, at any specific point. It’s the first step to calculate more complex charge distributions on 3D shapes and real-world devices, including sensors and capacitors.
In Class 12 Physics, this topic is too brief a section. But there is more to uncover when preparing for entrances after CBSE boards, such as CUET, or moving into electrical engineering. Today, we help you learn about electric potential at a point due to a point charge. We will cover the NCERT derivation, as well as its extended applications, below.
- What is Electric Potential at a Point Due to a Point Charge?
- NCERT Derivation of Potential Due to a Point Charge Class 12
- Derivation of Potential Due to a Point Charge
- Potential Due to a Ring
- Potential Due to Uniformly Charged Disc
- Potential Due to Uniformly Charged Spherical shell
- Potential Due To Uniformly Charged Solid Sphere
What is Electric Potential at a Point Due to a Point Charge?
Electric potential at a point due to a point charge is the amount of work needed to bring a tiny test charge from very far away (infinity) to a specific point near a source charge, without any acceleration. The electric potential at that point due to a point charge depends on two factors.
- How large the source charge is (larger charge = higher potential at the same distance)
- How far the point is from it (closer points have higher potential)
Whether you want to delve deeper or simply brush up, here are two observations.
- Tiny Test Charge: It’s a hypothetical, infinitesimally small charge. It’s used to probe an electric field without disturbing it.
- Source Charge: This is the charge that creates the electric field or potential being investigated. The typical representation is Q.
Importance of Learning Electric Potential Due to a Point Charge
- Electric potential due to a point charge requires knowledge of derivatives to tackle questions on JEE Main. The previous year questions include those of finding the potential difference between two points and calculating the potential energy of systems with point charges.
- This is a concept that is quite interrelated, connecting Gauss' Law and other principles of electromagnetism to derive equations. You may quickly refer to the relationship between electric field and electric potential. Or, even revisit NCERT Solutions for Chapter 1 in Class 12 Physics.
NCERT Derivation of Potential Due to a Point Charge Class 12
Section 2.3 of Chapter Two, Electrostatic Potential and Capacitors, contains the derivation of potential due to a point charge.
This is the definition of potential due to a point charge, as per the NCERT book.
“..the potential at P due to the charge Q is
".
Explanation of the NCERT Derivation for Electric Potential Due to a Point Charge
To derive this, the NCERT book primarily uses Coulomb’s Law and work equations.
Let’s understand how and why.
1. Coulomb Force (Equation 2.5 in NCERT)
We can consider that the electrostatic force on a unit positive charge at distance r' from charge Q is
F = Q/(4πε₀r'²) r̂'
Why so?
This equation comes from Coulomb's law. The force has some key characteristics.
- It's proportional to the charges (Q × 1 for unit test charge)
- The same is also inversely proportional to the square of the distance (1/r'²)
- Based on the law, force directs radially outward (repulsive for like charges)
- The unit vector r̂' shows direction along the line from Q to the test charge
2. Work Done for Small Displacement (Equation 2.6 in NCERT)
ΔW = -Q/(4πε₀r'²) Δr'
Why are we introducing the equation of work?
In the Class 11 Chapter on Work, Energy, and Power, we found that the Work done against a force has the mathematical representation as
So as we're moving radially inward (against the repulsive force), Δr' < 0
The dot product
This gives the negative sign, making ΔW positive (work must be done against repulsion).
If you are considering testing your old knowledge before our competitive exams, go practice NCERT Solutions for Chapter 5.
3. Total Work Done (Equation 2.7 in NCERT)
Now we use integration to calculate work, which is necessary to understand the distance between infinity and the final point. We also need to apply limits.
W = -∫[∞ to r] Q/(4πε₀r'²) dr' = Q/(4πε₀r')|[∞ to r] = Q/(4πε₀r)
What's the reasoning behind this?
So, we can now integrate how work goes up in increments between two points, i.e., from infinity (r' = ∞) to final position (r' = r)
∫(1/r'²)dr' = -1/r' (standard integral)
By applying limits, we get [-1/r - (-1/∞)] = [-1/r - 0] = -1/r
The overall negative sign will cancel out as -Q/(4πε₀) × (-1/r) = Q/(4πε₀r)
4. Electric Potential (Equation 2.8 in NCERT)
V(r) = Q/(4πε₀r)
Since we used a unit test charge, the work done equals the potential directly.
Derivation of Potential Due to a Point Charge
Derivation of the expression for potential due to point charge Q, at a point which is at a distance r from the point charge.
From definition of potential
Finding potential due to continuous charges
If formula of is tough, then we take a small element and integrate
If formula of is easy then, we use
(i.e. for sphere, plate, infinite wire etc.)
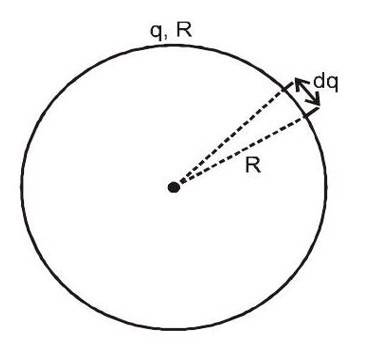
Potential Due to a Ring
(i) Potential at the centre of uniformly charged ring:
Potential due to the small element dq
∴ Net potential:
(ii) For non-uniformly charged ring potential at the center is
(iii) Potential due to half ring at center is:
(iv) Potential at the axis of a ring: Calculation of potential at a point on the axis which is a distance from centre of uniformly charged (total charge Q ) ring of radius R .
Consider an element of charge dq on the ring. Potential at point due to charge dq will be
Net potential at point
due to all such element will be :
Potential Due to Uniformly Charged Disc
, where
is the charge density and
is the distance of the point on the axis from the center of the disc
is the radius of disc.
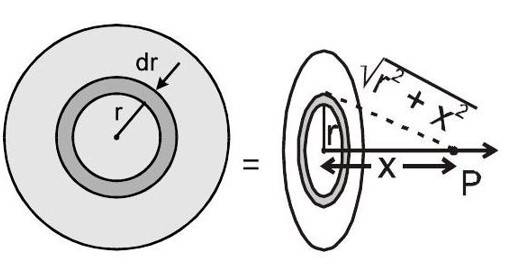
Finding potential due to a uniformly charged disc:
A disc of radius '
' has surface charge density (charge/area)
. We have to find potential at its axis, at point ' P ' which is at a distance x from the centre.
For this, we can divide the disc into thin rings and let's consider a thin ring of radius
and thickness
. Suppose charge on the small ring element
. Potential due to this ring at point '
' is:
So, net potential :
Here, charge area
So, area
Here, area of the small ring element length of ring width of the ring
So,
To integrate it, let
. Substituting we will get :
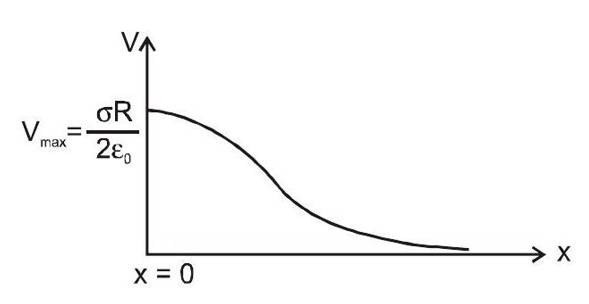
If a test charge is placed at point , then potential energy of this charge due to the disc
Graph of
v/s
at
to check whether V will increase with x or decrease, lets multiply and divide by conjugate.
Now, we can say that as so curve will be
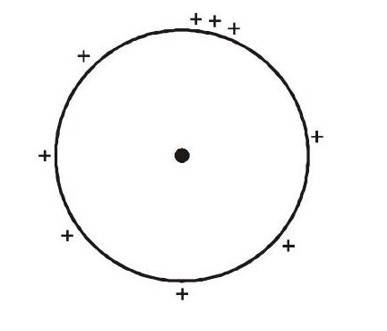
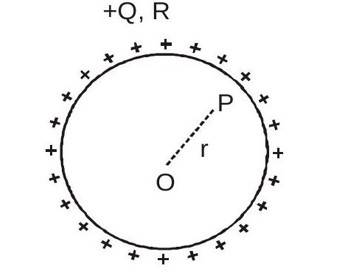
Potential Due to Uniformly Charged Spherical shell
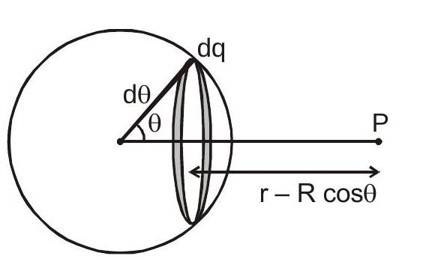
Derivation of expression for potential due to uniformly charged hollow sphere of radius
and total charge
, at a point which is at a distance
from centre for the following situation
(i)
(ii)
Assume a ring of width at angle from axis (as shown in figure). Potential due to the ring at the point will be
Where
where
then, net potential
Solving this eq. we find
(for
)
&
for
Alternate Method : As the formula of
is easy, we use
(i) At outside point
For outside point, the hollow sphere acts like a point charge.
(ii) Potential at the centre of the sphere : As all the charges are at a distance from the centre,
So,
(iii) Potential at inside point (
) : Suppose we want to find potential at point P , inside the sphere.
Potential difference between Point P and O :
Where,
So
Potential Due To Uniformly Charged Solid Sphere
Derivation of expression for potential due to uniformly charged solid sphere of radius R and total charge
(distributed in volume), at a point which is at a distance
from centre for the following situations.
(i)
(ii)
Consider an elementary shell of radius
and width
(i) For
(ii) For
From definition of potential
(i) For
(ii) For
Physics Electrostatic Potential and Capacitance Exam
Student Forum
Other Topics under this Chapter
- Overview
- Combination of Capacitors
- Electrostatic Potential
- Electrostatics
- Potential Due to Point Charge
- Energy Stored in a Capacitor
- Capacitors and Capacitance
- Effect of Dielectric on Capacitance
- Electrostatics of Conductors
- Potential Energy of a System of Charges
- Potential due to a System of Charges
- Potential Energy in an External Field
- Parallel Plate Capacitor
- Dielectrics and Polarisation
- Equipotential Surfaces
Other Class 12th Physics Chapters
- Physics Alternating Current
- Physics Ray Optics and Optical Instruments
- Physics Electromagnetic Induction
- Physics Dual Nature of Radiation and Matter
- Physics Semiconductor Devices
- Physics Wave Optics
- Physics Current Electricity
- Physics Nuclei
- Physics Electrostatic Potential and Capacitance
- Physics Atoms
- Physics Moving Charges and Magnetism
- NCERT Class 12 Notes
- NCERT Class 12 Physics
- Physics Electric Charge and Field
- Physics Electromagnetic Waves
- Physics Magnetism and Matter