Potential Due to a System of Charges: For Point Charges and Continuous Charge Distribution

The superposition principle in physics is used whenever you want to find the result of the interaction between two or more forces in a linear system. (You may recall using the superposition principle of waves). The result we get is through an algebraic or vector sum of the individual forces, depending on their scalar or vector nature.
In the Electrostatic Potential and Capacitance chapter, we are dealing with forces in the electric field, which also obey this superposition rule.
We’re dealing with multiple charges here, and the resultant electric field (E_net) they together create is the vector sum of the fields from each charge.
This approach is a direct consequence of Coulomb’s Law. In rudimentary vector form, this law shows the Coulomb force between two point charges (q_1 and q_2) separated by a distance r as 

F = k x (q_1q_2) x 1/r^2 x r

But in reality, the total force on a charge in the presence of other charges in the system is the vector sum of all the individual forces that together act on it.
If you went through our detailed topic explanation on the forces between multiple charges, which shows the additivity property, you will know that the force on charge 1 is due to charges 2, 3, and so on up to n.

F_net = F_12 + F_13 + F_14 +...+ F_1n

Going back, NCERT in the first Class 12 physics chapter establishes the fact that the electric field that one charge creates, remains independent of other charges in the field. 

This is because you learn the electric field at a specific point with the expression, E = F/q, which explains the force experienced per unit positive charge at that very point. 

Remember this is the property of how source charges are arranged, and not really about the test charge q.
You change the value of test charge q, the ratio of F/q remains the same. So, E or the electric field does not depend on the test charge. 

So for a quick example, if we’re to calculate the total field three source charges (q_1, q_2, and q_3) are exerting, we would sum those fields

E_net = E_1 + E_2 + E_3

Electric Field’s Relation to Electric Potential Due to a System of Charges

Hoping you’re clear until here on how electric field obeys the superposition principle.
Now, when we are talking about electrostatic potential, by definition, it is the work done by the electric field.  And if we’re able to find the electric field by superposition principle, it also means we can use this principle to find the potential due to a system of charges.
What’s more convenient to know is that electrostatic potential is NOT a vector, because work done is a scalar quantity. Instead of tedious and complicated vector addition, we will be using simple algebraic summation using the same superposition principle. 

By understanding the Coulomb’s Law again here, we’re treating each source charge as independent. In this calculation, we look at the source charge magnitude and the position, as well as the field point. Only after finding the individual fields, you can combine them using superposition.

What is the electric potential due to a system of charges then?

If the source charges are q_1, q_2, q_3 and the test charge is q, the superposition applied below for total or net electric potential, a scalar quantity, will be

V_net = V_1 + V_2 + V_3

Here, we’re treating each source charge having its own field. We are not considering the affect of other charges, as they would have their own individual fields.
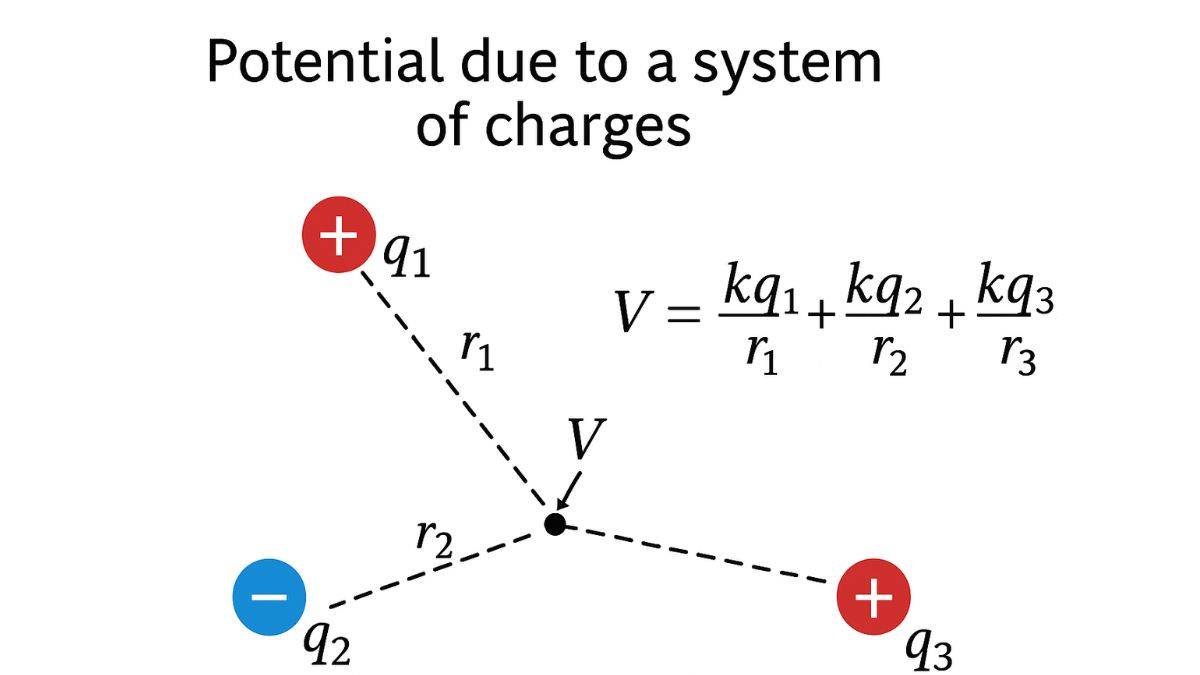
The expression of a potential due to a point charge q_1 at a distance r_1 is

V(r_1) = kq_1/r_1

Similarly for q_2 and q_3, the equations of potential will be

V(r_2) = kq_2/r_2 and V(r_3) = kq_3/r_3

The distances r_1, r_2, and r_3 are also different as each charge is located at different positions with respect to the test charge. We can assign the point of the test charge to be P. (Note, in your NCERT textbook, you will find r_1 as r_1P. It means the same and only specifies the distance between q_1 and R_1)
k is the constant throughout, and you can learn why in our article about the value of k in electrostatics. 

For now, if we are to expand on the total electric potential due to a system of charges at a point P, we get,

V_P = k (q_1/r_1 + q_2/r_2 + q_3/r_3)

This is the main equation of potential due to a system of charges when the superposition principle is applied. There are plenty of problems to practice with this on electrostatic potential and capacitance NCERT Solutions.

Until here, you learnt about the potential of a test charge at an arbitrary point in relation to point charges. How would you deal with this calculation when multiple charges are spread across a line, surface, or volume?
The deal is, the calculation will become incorrect if you leave it at

V_P = k (q_1/r_1 + q_2/r_2 + q_3/r_3)

It will not hold true if the charge is spread along a wire, a sheet, and sphere, as each of them has a different charge density.
Continuous charge distribution is more common in the real world objects and surfaces, and you learnt that linear charge distribution (usually considered as a one-dimensional calculation over length), will differ in charge density from surface charge (area with two sides) and volume charge (three-dimensional). 

We cannot treat such types of charge spreads as point charges.
Instead we focus on taking a small sample of the surface and treat that as a point charge to approximate, that is, differentials and then move to the integral form to get the whole picture.
If the charge spread is linear, recall the formula of linear charge distribution, λ = dq/dl, so a small section of this charge will result in dq = λdl 

When at surface level, we know the surface charge distribution is 𝜎 = dq/ds, for which we get dq = 𝜎ds

For volume, that is ρ = dq/dv, equating to dq = ρdv
Now we’re getting somewhere. 

The total electric potential due to a system of charges for a linear spread. 

Using dq = λdl in the electrostatic potential equation and integrate for the surface
V = k ∫λdl/r

Same for surface and volume, we equate to
V = k ∫𝜎ds/r (surface)
V = k ∫ρdv/r (volume)

Gain more mastery across PCM Class 12 with these.  

Complete CBSE Class 12 Study Material
NCERT Class 12 Maths Solutions	NCERT Physics Class 12 Solutions	Class 12 Chemistry NCERT Solutions
Class 12 Maths NCERT Notes	Physics Class 12 NCERT Notes	Class 12 Chemistry NCERT Notes
CBSE Sample papers for class 12 Maths	CBSE Class 12 Physics Sample Papers	CBSE Class 12 Sample Paper for Chemistry
CBSE Class 12 Maths Previous Year Question Papers	CBSE Class 12 Physics Previous Year Question Papers	CBSE Chemistry Class 12 Question Papers