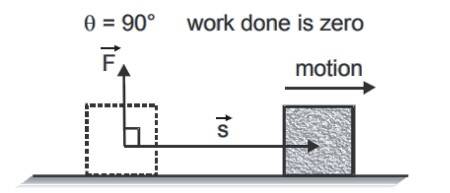
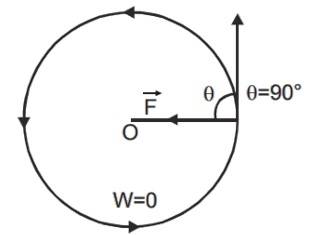
The definition of work in physics is different from that in everyday usage. The fifth chapter of your Class 11 Physics textbook, Work, Energy, and Power, defines work as energy transfer through force that causes displacement.
This guide explores Work in physics as a scalar quantity with constant and variable forces. We have made it as detailed as you need to secure solid marks in your annuals. With it, you can easily practise most of the chapter 5 NCERT Solutions of Class 11.
- What is Work in Physics?
- NCERT Definition of Work
- Work Done by a Constant Force
- Work Done by a Variable Force
- Calculating Work from Graph
- Types of Work | Nature of Work Done
- Dependency on Frame of Reference
- Unit and Dimensions of Work in Physics
What is Work in Physics?
In physics, work is done only when a force moves something.
That means two things.
- You apply force to an object, such as a box
- The object (the box) moves or displaces in the direction of the force
There is no work without movement, even after pushing an object hard.
Let’s see how we represent that in physics!
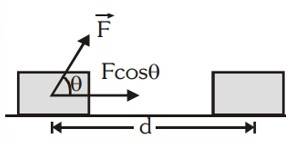
Whenever a force acts on a body and displaces it, work is said to be done (by the force).
Mathematically, work done by a constant force is equal to the scalar product of the force, i.e.,
applied and the displacement of the point of application,
Here it how it looks visually.
NCERT Definition of Work
Section 5.3 of the Chapter - Work, Energy and Power, defines work after briefly explaining about Scalar Products and the Work Energy Theorem.
It does so because with scalar products, you get to learn what is work is in terms of dot product of force and displacement vectors. The textbook also touches upon the theorem to show the direct link between the work done on an object and the changes in its kinetic energy.
So the NCERT definition of work is
"The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement. Thus W = (F cos θ )d = F.d"
Some important points that follow along this textbook definition of work are below.
- Work is a scalar. It means that it has magnitude but no direction.
- If the object does not move, it is not work. But it could be a situation when the force is perpendicular to the displacement - even then it would be zero work.
- It's called positive work, when force and displacement are in the same direction.
- It would be negative work, when force and displacement are opposite to each other.
So, these are all you need to know when work is done and when it isn't. Let's show you how to calculate work in different situations. Follow along the next sections!
Work Done by a Constant Force
Let's understand work done by a constant force.
When the direction and magnitude of a force applied to a body is constant, the force is said to be constant.
Mathematically, it shows this way.
Work done by a constant force,
Force
component of displacement along the force
i.e., work done will, be
In vector form,
Note: The force of gravity (within small altitudes) serves as an example of a constant force.
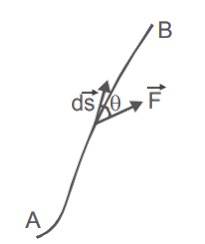
Work Done by a Variable Force
When the force applied to a body is changing in direction or magnitude or both, the force is variable.
Let's see how to calculate work done by a variable force.
Suppose a variable force causes displacement of a body from position to position . To calculate the work done by the force, the path from to can be divided into infinitesimal elements.
Each element is so small that during the displacement of the body through it, the force is considered constant. If dr be the small displacement of the point of application and be the force acting on the body, the work done by force is
The total work done in displacing the body from to is given by
If
and
be the position vectors of the points
and
respectively then the total work done
Cartesian Form
When the magnitude and direction of the force varies with position, work done by the force for infinitesimal displacement
is
The total work done for the displacement from position to is In terms of rectangular components
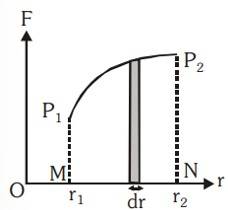
Calculating Work from Graph
Suppose a body, whose initial position is , is acted upon by a variable force and consequently the body acquires its final position . From position to or for small displacement , the work done will be whose value will be the area of the shaded strip of width .
The work done on the body in displacing it from position to will be equal to the sum of areas of all such strips
Thus, total work done,
Area of
The area of the graph between curve and displacement axis is equal to the work done.
Note : To calculate the work done by graphical method, for the sake of simplicity, here we have assumed the direction of force and displacement as same, but if they are not in same direction, the graph must be plotted between and r .
Types of Work | Nature of Work Done
A basic formula for positive work is below.
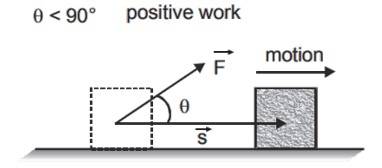
If the angle
is acute
then the work is said to be positive. Positive work signifies that the external force favours the motion of the body.
- When a body falls freely under the action of gravity , the work done by gravity is positive.
- When a spring is stretched, stretching force and the displacement both are in the same direction. So work done by stretching force is positive.
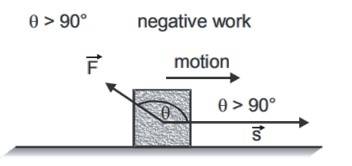
Negative work
If the angle
is obtuse (
).
Then the work is said to be negative.
It signifies that the direction of force is such that it opposes the motion of the body.
- Work done by frictional force is negative when it opposes the motion.
- Work done by braking force on the car is negative.
Zero work
Work done will be zero if or or
Some examples of zero work are below.
- body moving with uniform velocity.
- net force on the particle is zero.
- we push the wall, and it remains at rest.
- a pendulum is oscillating, work done by tension.
- electron is moving round the nucleus.
- satellite is moving around the earth.
- coolie "Sahayak" is carrying baggage on a horizontal platform (W.D. by gravitational force is zero)
Dependency on Frame of Reference
A force does not depend on frame of reference and assumes the same value in all frame of references. But displacement depends on frame of reference and may assume different values relative to different reference frames.
So, the work of a force depends on choice of reference frame.
For example, consider an individual with a suitcase standing in a lift that is moving up. In the reference frame attached to the lift, they apply a force equal to the weight of the bag. But the displacement of the bag is zero. So, the work due to this force on the bag is zero.
But, also know, that in a reference frame attached to the ground the bag has displacement equal to that of the lift and the force applied by this individual does a non-zero work.
Unit and Dimensions of Work in Physics
Physics Work, Energy and Power Exam
Student Forum
Other Topics under this Chapter
- Disadvantages of Biogas
- Concept of Potential Energy
- Power
- Potential Energy of Spring
- Conservation of Mechanical Energy
- Kinetic Energy
- Collision
- Work
- Types of Potential Energy
- Derivation of Work Energy Theorem
- Derivative of Potential Energy
- Elastic Potential Energy
- Thermal Power Plant Diagram
- Kinetic Energy and Potential Energy
- Derivation of Kinetic Energy
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test