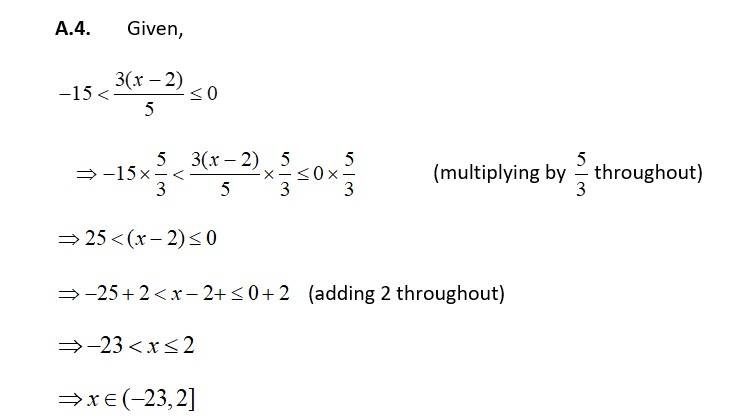In the Linear Inequalities Class 11 NCERT solutions, the students will study the linear inequalities in one and two variables. The concepts are extremely important for solving problems in mathematics, science, statistics, psychology, economics, etc. The Linear Inequalities Class 11 Chapter covers the Inequalities, and Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation.
Class 11 Linear Inequalities solutions are designed by the subject matter experts at Shiksha. The solutions given here are step-by-step and reliable. Students must study from these solutions to get a high score in the Class 11 exams and other competitive exams later on. The solutions are well-designed to improve students' problem-solving skills.
The Class 11 science students looking for the NCERT notes of all chapters of Maths can explore them here. They will also get the important topics and solved examples.
- Quick Overview of NCERT Solutions for Class 11 Maths Chapter 5: Linear Inequalities
- Class 11 Math Linear Inequalities: Key Topics, Weightage
- Important Formulas of Class 11 Linear inequalities
- Class 11 Maths Chapter 5 Linear Inequalities NCERT Solutions PDF – Free Download
- Class 11 Math Linear Inequalities Exercise 5.1 NCERT Solutions
- Class 11 Math Linear Inequalities Exercise 6.2 NCERT Solutions (Old NCERT)
- Class 11 Math Linear Inequalities Exercise 6.3 NCERT Solutions (OLD NCERT)
- Class 11 Math Linear Inequalities Miscellaneous Exercise Solution(Old NCERT)
Quick Overview of NCERT Solutions for Class 11 Maths Chapter 5: Linear Inequalities
Here is a snapshot of the Class 11 Linear Inequalities:
- Linear Inequalities Class 11 states that two algebraic expressions or real numbers related by the following symbols - form an inequality.
- In such a case, the same numbers can be added to or subtracted from both sides of an inequality.
- Both sides of the inequality can be multiplied or divided by the same positive number, but when multiplied or divided by a negative number, the condition of inequality is reversed.
To get the Physics, Chemistry, and Maths NCERT Class 11 notes in one place for quick revision, check here.
Class 11 Math Linear Inequalities: Key Topics, Weightage
Class 11 Linear Inequalities is an important chapter from the JEE Mains point of view, as this chapter falls under the broader category of Algebra in the JEE Main syllabus. See below the topics covered in this chapter:
| Exercise | Topics Covered |
|---|---|
| 5.1 | Introduction |
| 5.2 | Inequalities |
| 5.3 | Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation |
Linear Inequalities Class 11 Weightage in JEE Mains
| Exam | Weightage |
|---|---|
| JEE Mains | Linear Inequalities from Class 11 come under Algebra and carry 35% to 40% weightage of Algebra. |
Important Formulas of Class 11 Linear inequalities
Important Formulae of Linear Inequalities for CBSE Examination
General Forms of Linear Inequalities
-
One Variable:
where a, b are real numbers, a ≠ 0, and x is a variable.
-
Two Variables (Linear Inequality Equation):
where a, b, c are real numbers, and x, y are variables.
Graphical Representation Rules
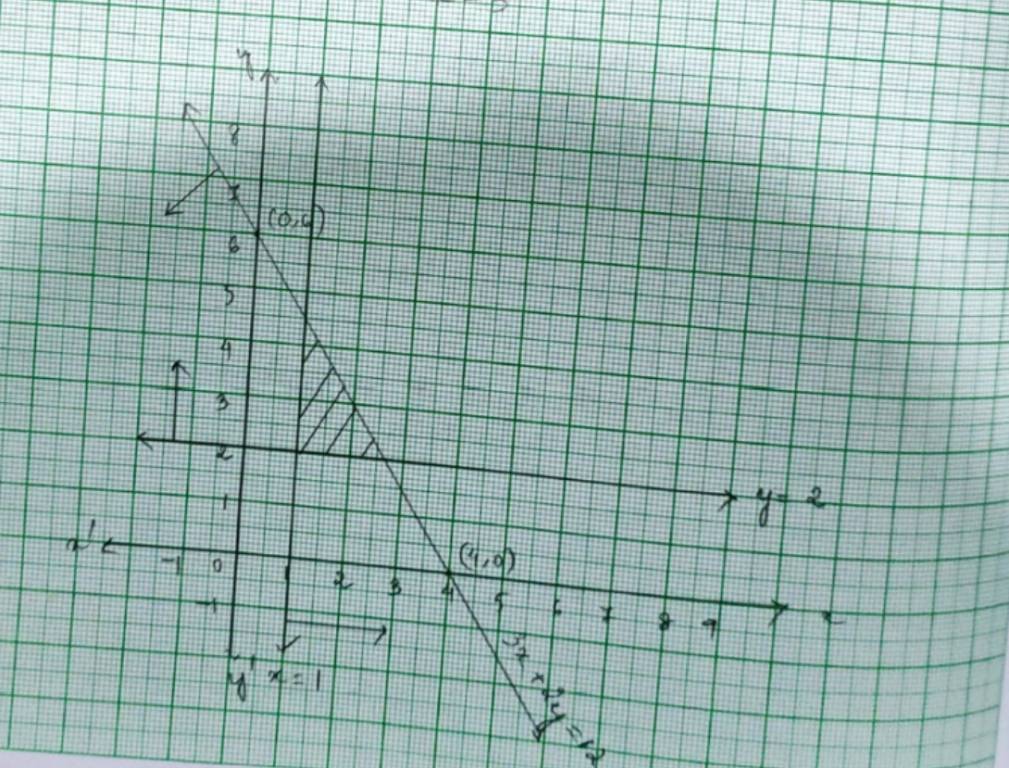
- Convert inequality to equation: ax + by = c (treat as an equation for plotting).
- Find x- and y-intercepts and plot the boundary line.
- Shading the Region:
- If y > mx + c, shade the upper region.
- If y < mx + c, shade the lower region.
Class 11 Maths Chapter 5 Linear Inequalities NCERT Solutions PDF – Free Download
A free Linear Inequality Class 11 PDF is given below for students to download. The well-written PDF helps students to understand the concepts properly and apply them while answering the NCERT textbook questions.
Class 11 Maths Chapter 5 Linear Inequalities NCERT Solutions: Free PDF Download
Other Links
| NCERT Notes for Class 11 & 12 | NCERT Solutions for Class 11 Maths | NCERT Solutions Class 11 and 12 for Maths, Physics, Chemistry |
Class 11 Math Linear Inequalities Exercise 5.1 NCERT Solutions
Exercise 5.1 focuses on fundamental concepts of Linear Inequalities such as the basics of algebraic expressions involving greater than ( > ), less than ( < ), greater than or equal to ( ≥ ), and less than or equal to ( ≤ ) symbols. Class 11 ch 6 exercise 5.1 also helps students differentiate between equations and inequalities and represent inequalities on a number line. Exercise 5.1 consists of 26 questions, all solutions are provided below;
Class 11 Math Linear Inequalities 5.1 SolutionQ1. Solve 24x < 100, when(i) x is a natural number. (ii) x is an integer. |
| A.1. 24x < 100. Dividing both sides by 24 we get,
x< = 4.166 (i) As x is a natural no the soln of the given inequality are 1, 2, 3, 4. (ii) As x is an integer the soln of the given inequality are 4, 3, 2, 1, 0, 1, 2, 3, …. |
| Q2. Solve – 12x > 30, when (i) x is a natural number. (ii) x is an integer. |
| A.2. – 12 x> 30. Dividing both sides by 12 we get,
Multiplying both side by ( – 1) the inequality will change. i e, x< = – 2.5 (i) As x is a natural number, the soln of the given inequality does not exist in natural numbers. (ii) As x is an integer, the soln of the given inequality will be all the integer less than – 5/2 i. e, – 3, – 4, – 5, ….. |
| Q3. Solve 5x – 3 < 7, when (i) x is an integer. (ii) x is a real number. |
| A.3. Given, 5x – 3 < 7. 5x – 3 + 3 < 7 + 3 5x< 10
x< 2. when x∈z, i. e, x is an integer all integers less than 2 are the soln so, x = {…., – 3, – 2, – 1, 0, 1} (ii) when x ∈ R i, e x is a real number all t real number less than 2. are the soln. So, x∈ (– ∞, 2) |
| Q4. Solve 3x + 8 >2, when (i) x is an integer. (ii) x is a real number. |
| A.4. Given, 3x + 8 > 2 3x + 8 – 8 > 2 – 8 3x> – 6
x> – 2 (i) when x is an integer, x ∈ z all integer greater than – 2 are the soln. so, x = { – 1, 0, 1, 2, 3, …}. (ii) when x is a real number, all real number greater than – 2 are the soln. so, x ( –2,∞ ) |
| Solve the inequalities in Exercises 5 to 16 for real x. Q5. 4x + 3 < 5x + 7 |
| A.5. Given, 4 x+ 3 < 5 x+7. 3–7<5 x –4 x. –4
So, x ( –4,∞) |
| Q6. 3x – 7 > 5x – 1 |
| A.6. Given, 3x–7 > 5x–1. 7+1> 5x–3x 6> 2x
–3 > x So, x ∈(–∞,– 3) |
| Q7. 3(x – 1) ≤ 2 (x – 3) |
| A.7. 3(x –1) ≤ 2(x –3) 3x– 3 ≤ 2x –6 => 3x– 2x ≤ –6 + 3 x ≤ –3 So, x ∈(–∞,– 3] |
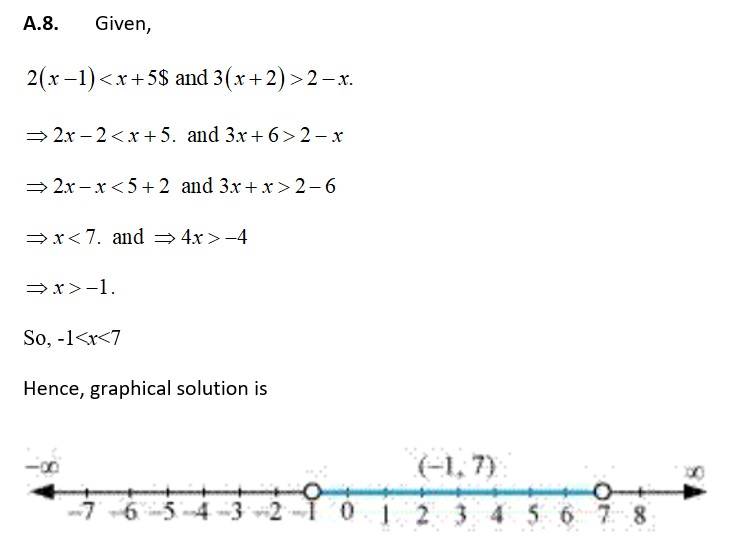
| Q8. (2 – x) ≥2 (1 – x) |
| A.8. 3(2 – x) ≥2(1 – x) 6 – 3x ≥ 2 – 2x 6– 2≥ 3x– 2x 4≥ x So, x∈ (–∞, 4] |
| Q9. |
| A.9. x + < 11
11x< 66
x< 6. So, x∈ (–∞, 6) |
| Q10. |
| A.10. Given,
x> 6 x< –6. So, x (–∞, –6) |
| Q11. |
| A.11. Given, => 3 x 3(x – 2) ≤ 5 x 5(2 – x) => 9x – 18 ≤ 50 – 25x => 9x + 25x ≤ 50 + 18 => 34x ≤ 68 => => x ≤ 2 So, |
| Q12. |
| A.12. Given,
x ≥–120. (–1) x (–x)≤ ( –120)× (–1) x ≤ 120. So, x ∈(–∞, 120]. |
| Q13. 2 (2x + 3) – 10 < 6 (x – 2) |
| A.13. Given 2 (2x + 3) –10 < 6 (x –2) 4x + 6 –10 < 6x– 12. 4x –4 < 6x –12 12 –4 < 6x –4x 8 < 2x
So, x∈ (4, –∞) |
| Q14. 37 – (3x + 5) ≥ 9x – 8 (x – 3) |
| A.14. Given, 37 –(3x + 5) ≥9x –8 (x –3) 37– 3x–5 ≥9x –8x+ 24. 37 – 24–5 ≥9x –8x+ 3x 8 ≥4x.
2 ≥x So, x∈ (–∞, 2] |
| Q15. |
| A.15. Given,
15x<4[25x–10–21x+9] 15x< 4 [4x –1] 15x< 16x–4 4 < 16x –15x 4. <. x So, x ∈(4,∞ ) |
| Q16. |
| A.16. Given,
20(2x- 1) ≥3 [15x- 10 - 8 + 4x]. 40x-20 ≥3[19x-18] 40x-20 ≥ 57x – 54. 54 - 20 ≥ 57x- 40x 34 ≥17x
2 ≥x So, x(- ∞, 2]. |
| Q17. 3x – 2 < 2x + 1 |
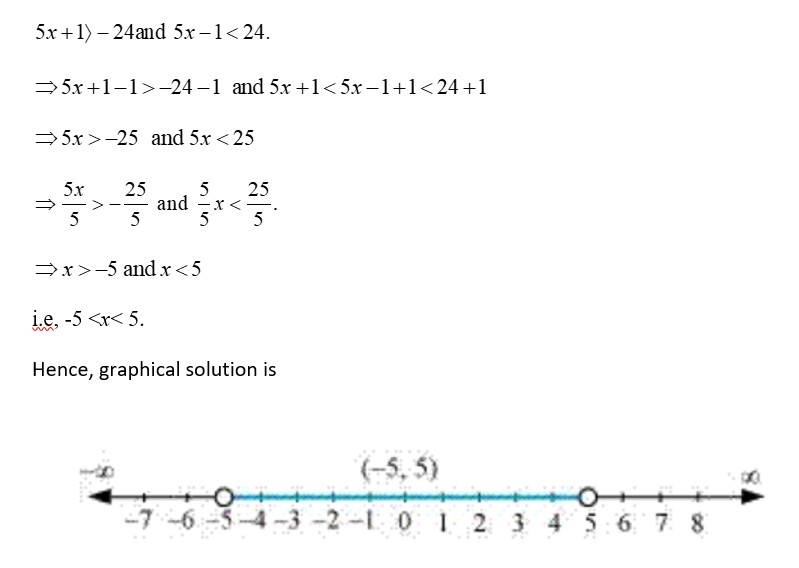
| A.17. Given, 3x – 2 < 2x + 1 3x – 2x< 2 + 1 x< 3. So, x (- ∞, 3).
|
| Q18. 5x – 3 > 3x – 5 |
| A.18. Given, 5x – 3 > 3x 5 5x –3x≥ –5 + 3. 2x ≥ –2. x x ≥ –1. So, x [1,- ∞ ).
|
| Q19. 3 (1 – x) < 2 (x + 4) |
| A.19. Given, 3(1–x) < 2(x + 4) 3 –3x< 2x + 8 3–8< 2x+ 3x –5 < 5x
-1
So, x ∈ (–1,∞ )
|
| Q20. |
| A.20. Given,
15x ≥2[25x –10 –21x + 9]. 15x ≥2[4x –1] 15x≥ 8x –2 15x –8x ≥–2 7x ≥–2 x ≥ So, x
|
| Q21. Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks. |
| A.21. Let x be the marks obtained by Ravi in third test. Then, average mark≥ 60
145 + x≥ 180. x ≥180 - 145 x≥ 35. So minimum mark required = 35. |
| Q22. To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course. |
| A.22. Let ‘x’ be the marks obtained by Sunita in the 5th exam. Then, average marks ≥ 90. . 368 + x ≥90 × 5. 368 + x ≥450. x ≥ 450 - 368. x.≥ 82. Minimum mark required= 82. |
| Q23. Find all pairs of consecutive odd positive integers both of which are smaller than10 such that their sum is more than 11. |
| A.23. Let x be the smaller of the consecutive odd positive integers, then the. other is x + 2 {Since the consecutive odd number are differ by 2.} then the. other is x + 2 so, x< 10 and x + 2 < 10 x< 8 and x + (x + 2) > 11. 2x> 11 - 2 2x> 9
and hence, 4.5
As x∈z, x = 5 and x = 7 and x is odd The reqd. possible pairsby (x, x + 2) are (5, 7),(7, 9). |
| Q24. Find all pairs of consecutive even positive integers, both of which are larger than5 such that their sum is less than 23. |
| A.24. Let x be the smaller no. of the two consecutive even positive integers, hence the other number is x + 2.(Two consecutive even no. differs by 2). Then, x> 5, x + 2 > 5 =>a> 3. And x +(x + 2) < 23 2x + 2 < 23 2x< 23 - 2 2x< 21
So, 5
Hence, x can take the value 6, 8 and 10. So, the required possible pair is given by (x, x + 2) are (6, 8), (8, 10) and (10, 12). |
| Q25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side. |
| A.25. Let x cm be the shortest side of the triangle. Thus, the other 2 sides are “3x”cm and “3x - 2”. cm Given, perimeter of A triangle ≥ 61 x + 3x - 3x- 2 ≥61 7x - 21≥ 61 7x ≥ 61 + 21
x ≥ 9. The minimum length of the shortest side is 9 cm. |
| Q26. A man wants to cut three lengths from a single piece of board of length 91cm.The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second? [Hint: If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x ≤ 91 and2x ≥ (x + 3) + 5]. |
| A.26. Let ‘x’ cm be the length of shortest piece. Then, the two other remaining length is. (x + 3) cm and (2x). cm. So, given that, 2x - (x + 3) ≥ 5 cm. 2x- x - 3 ≥ 5. x ≥ 5 + 3 x ≥ 8. And. total length ≤ 91 cm x + (x + 3) + 2x ≤ 91 4x + 3 ≤ 91 4x + 3 ≤ 91 - 3
x ≤ 22. ⸫ 8 ≤ x ≤ 22. Hence the length of the shortest board is greater than or equal to 8 cm and less than or equal to 22 cm. |
Commonly asked questions
39. 2x + y ≥ 6, 3x + 4y < 12
39.The given system of inequalities is
2x+y ≥ 6 - (1)
3x+4y ≤ 12- (2)
The corresponding equations are
2x + y = 6
and 3x + 4y = 6
So,
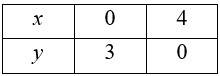
Put (x, y)= (0,0) in (1), (2),
? 2 × 0+0 ≥ 6
0 ≥ 6 which is false.
And 3 × 0+4 × 0 ≤ 12
0 ≤ 12 which is true.
So, solution of inequality (1) lies on the plane which excludes the origin and the solution of inequality (2) lies on the plane which includes the origin.
So, the required solution of the given system of inequality is the shaded region.
20.
20. Given,
15x ≥ 2 [25x –10 –21x + 9].
15x ≥ 2 [4x –1]
15x ≥ 8x –2
15x – 8x ≥ –2
7x ≥ –2
x ≥
So, x
64. How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
64. Let x litre of water is required to added.
Then, total mixture =(x+1125) litre.
As, 0 % of acid is contained in pure mater (neutral).
0% of x + 45% of 1125% > 25% of (x+1125)
(multiplying by 100 throughout)
(dividing by 25 throughout)
……(1)
And 0% of x+ 45% of 1125<30 of (x+1125)
{multiplying by 100 throughout)
45 × 1125 – 30 × 1125 < 30x
{dividing by 30 throughout}
562.5 From (1) and (2), 562.5 Thus, the water to be added has to be more than 562.5 litre but less than 900 litres.
24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
24. Let x be the smaller no. of the two consecutive even positive integers, hence the other number is x + 2. (Two consecutive even no. differs by 2).
Then, x > 5, x + 2 > 5 => a> 3.
And x + (x + 2) < 23
2x + 2 < 23
2x < 23 - 2
2x < 21
So, 5 < x
Hence, x can take the value 6, 8 and 10.
So, the required possible pair is given by (x, x + 2) are (6, 8), (8, 10) and (10, 12).
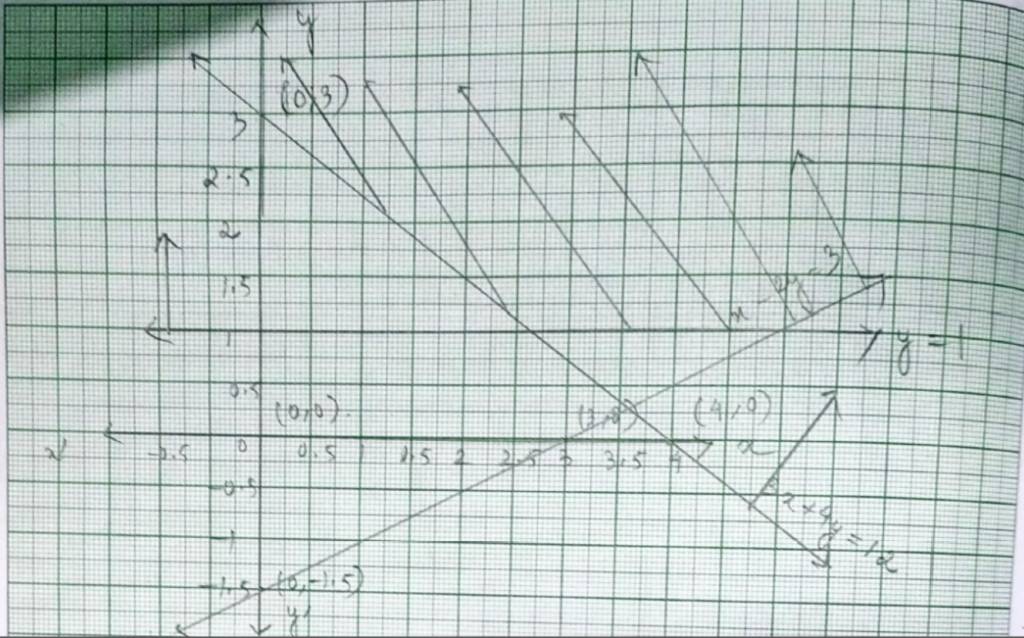
48. x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0 ,y ≥ 1
48. The given system of inequality is
x – 2y≤ 3 - (1)
3x – 4y≥12- (2)
x ≥ 0 - (3)
y≥ 1 - (4)
The corresponding equation of (1) and (2) are
x – 2y= 3
x | 3 | 0 |
y | 0 | –1.5 |
and 3x – 4y=12
x | 4 | 0 |
y | 0 | 3 |
Putting (x, y)= (0,0) in inequality (1) and (2),
0 – 2 × 0 ≤ 3 => 0 ≤ 3 is true.
and 3 × 0+4 × 0 ≥ 12 => 0 ≥ 12 is false.
So, solution of inequality (1) includes plane wilt origin (0,0) while solution plane of inequality (2) includes the origin.
∴ The shaded portion determines the solution region of the given system of inequality.
9.
9. x + < 11
11x < 66
x < 6.
So, x ∈ (–∞, 6)
11.
11. Given,
=> 3 x 3 (x – 2) ≤ 5 x 5 (2 – x)
=> 9x – 18 ≤ 50 – 25x
=> 9x + 25x ≤ 50 + 18
=> 34x ≤ 68
=>
=> x ≤ 2
So,
12.
12. Given,
x ≥–120.
(–1) x (–x)≤ ( –120)× (–1)
x ≤ 120.
So, x ∈ (–∞, 120].
26. A man wants to cut three lengths from a single piece of board of length 91cm.The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second?
[Hint: If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x ≤ 91 and2x ≥ (x + 3) + 5].
26. Let ‘x’ cm be the length of the shortest piece.
Then, the two other remaining length is.
(x + 3) cm and (2x). cm.
So, given that,
2x - (x + 3) ≥ 5 cm.
2x- x - 3 ≥ 5.
x ≥ 5 + 3
x ≥ 8.
And. total length ≤ 91 cm
x + (x + 3) + 2x ≤ 91
4x + 3 ≤ 91
4x + 3 ≤ 91 - 3
x ≤ 22.
? 8 ≤ x ≤ 22.
Hence the length of the shortest board is greater than or equal to 8 cm and less than or equal to 22 cm.
41. 2x – y >1, x – 2y < – 1
41. The given system of inequality is
2x – y> 1 - (1)
x – 2y< –1- (1)
So the corresponding equations are
2x – y=1
x | 0 | 0.5 |
y | –1 | 0 |
and x – 2y= –1
x | –1 | 0 |
y | 0 | 0.5 |
Putting (x, y)= (0,0) in (1) and (2) to cheek the inequality
2 × 0 – 0 > 1
0 > 1 which is not true.
and 0 – 2 × 0< –1
0< –1 which is not true.
So, the solution of plane of inequality (1)and (2) does not include the plane with point (0,0) or origin.
? The reqd. solution of the given system of inequality is the shaded region.

10. Kindly Consider the following
10. Given,
x> 6
x< –6.
So, x (–∞, –6)
63. A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution toit. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
63. Let x litre of 20 % boric acid solution is required to added. Since, we have 640 litres of 8 % boric acid solution.
Total mixture will have (x + 640) litre.
(multiplying throughout by )
(1)
And 2 % of x + 8 % of 640 < 6 % of (x+ 640)
So, from (1) and (2) we get,
320 Thus, the number of litre of 2 % boric acid solution will have to be more than 320 litres but less than 1280 litres.
65. IQ of a person is given by the formula
where MA is mental age and CA is chronological age. If 80 IQ 140 for a group of 12 years old child, find the range of their mental age.
It is given that,
IQ = …. (1)
and 80 IQ 140 ……. (2)
Putting (1) in (2) we get,
Let x be the mental age for chronological age 12, then we can write,
(multypling by 12/1200 throughout)
Thus, the required metal age for 12 yes old children is from 9.6 to 16.8.
2. Solve – 12x > 30, when
(i) x is a natural number.
(ii) x is an integer.
2. – 12 x> 30.
Dividing both sides by 12 we get,
Multiplying both side by ( – 1) the inequality will change.
i e, x< = – 2.5
(i) As x is a natural number, the soln of the given inequality does not exist in natural numbers.
(ii) As x is an integer, the soln of the given inequality will be all the integer less than – 5/2
i. e, – 3, – 4, – 5, ….
21. Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
21. Let x be the marks obtained by Ravi in third test.
Then, average mark ≥ 60
145 + x ≥ 180.
x ≥180 - 145
x ≥ 35.
So minimum mark required = 35.
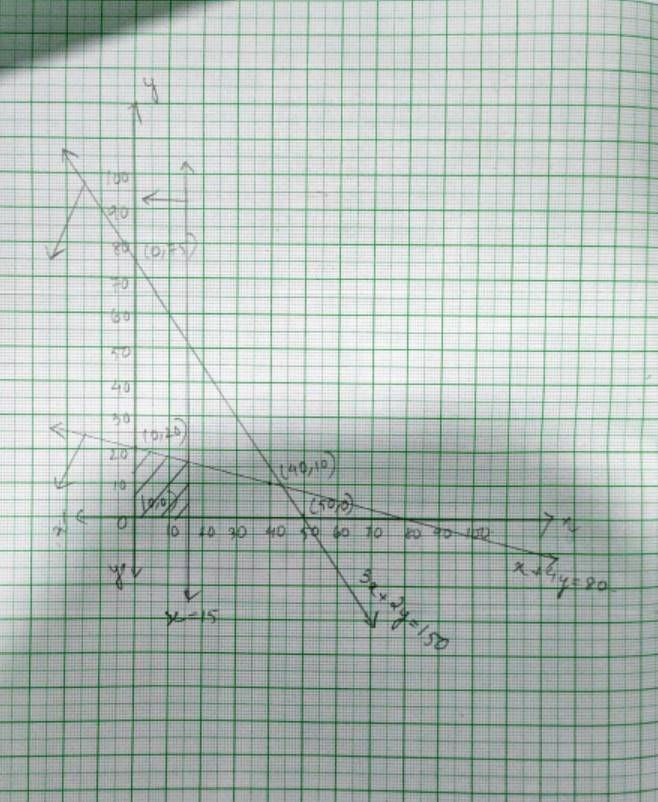
50. 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
50.The given system of inequality is
3x+2y≤ 150- (1)
x+4y≤ 80- (2)
x≤ 15 - (3)
y≥ 0 and x≥ 0 - (4)
The corresponding equation of (1) and (2) are
3x + 2y = 150
x | 50 | 0 |
y | 0 | 75 |
and x + 4y =80
x | 0 | 40 |
y | 20 | 10 |
Putting (0,0)= (x, y) in inequality (1) and (2) we get,
3 × 0+2 × 0 ≤ 150 => 0 ≤ 150 is true.
and 0+4 × 0 ≤ 80 => 0 ≤ 80 is true.
So, the solution plane of both inequality (1) and (2) includes the origin (0,0).
∴ The shaded region is the solution of the given system of inequality.
14. 37 – (3x + 5) ≥ 9x – 8 (x – 3)
14. Given, 37 – (3x + 5) ≥9x –8 (x –3)
37– 3x–5 ≥9x –8x+ 24.
37 – 24–5 ≥9x –8x+ 3x
8 ≥4x.
2 ≥x
So, x∈ (–∞, 2]
Class 11 Math Linear Inequalities 5.1 Solution
1. Solve 24x < 100, when
(i) x is a natural number.
(ii) x is an integer.
1. 24x < 100.
Dividing both sides by 24 we get,
x< = 4.166
(i) As x is a natural no the soln of the given inequality are 1, 2, 3, 4.
(ii) As x is an integer the soln of the given inequality are 4, 3, 2, 1, 0, 1, 2, 3, ….
3. Solve 5x – 3 < 7, when
(i) x is an integer.
(ii) x is a real number.
3. Given, 5x – 3 < 7.
5x – 3 + 3 < 7 + 3
5x< 10
x< 2.
(i) when x ∈ z, i. e, x is an integer all integers less than 2 are the soln so, x = {…., – 3, – 2, – 1, 0, 1}
(ii) when x ∈ R i, e x is a real number all t real number less than 2. are the soln so, x∈ (– ∞, 2)
4. Solve 3x + 8 > 2, when
(i) x is an integer.
(ii) x is a real number.
4. Given, 3x + 8 > 2
3x + 8 – 8 > 2 – 8
3x > – 6
x > – 2
(i) when x is an integer, x ∈ z all integer greater than – 2 are the soln. so, x = { – 1, 0, 1, 2, 3, …}.
(ii) when x is a real number, all real number greater than – 2 are the soln. so, x ( –2, ∞ )
Solve the inequalities in Exercises 5 to 16 for real x.
5. 4x + 3 < 5x + 7
5. Given,
4 x + 3 < 5 x+ 7.
3 – 7 < 5 x – 4 x.
–4 < x.
So, x ( –4, ∞)
6. 3x – 7 > 5x – 1
6. Given, 3x – 7 > 5x – 1.
7+1 > 5x – 3x
6 > 2x
–3 > x
So, x ∈ (–∞, – 3)
7. 3(x – 1) ≤ 2 (x – 3)
7. 3 (x –1) ≤ 2 (x –3)
3x– 3 ≤ 2x –6
=> 3x– 2x ≤ –6 + 3
x ≤ –3
So, x ∈ (–∞, – 3]
8. (2 – x) ≥ 2 (1 – x)
8. 3 (2 – x) ≥ 2 (1 – x)
6 – 3x ≥ 2 – 2x
6– 2 ≥ 3x– 2x
4 ≥ x
So, x ∈ (–∞, 4]
13. 2 (2x + 3) – 10 < 6 (x – 2)
13. Given 2 (2x + 3) –10 < 6 (x –2)
4x + 6 –10 < 6x– 12.
4x –4 < 6x –12
12 –4 < 6x –4x
8 < 2x
So, x∈ (4, –∞)
16.
16. Given,
20 (2x- 1) ≥3 [15x- 10 - 8 + 4x].
40x-20 ≥3 [19x-18]
40x-20 ≥ 57x – 54.
54 - 20 ≥ 57x- 40x
34 ≥17x
2 ≥x
So, x (- ∞, 2].
17. 3x – 2 < 2x + 1
17. Given, 3x – 2 < 2x + 1
3x – 2x< 2 + 1
x< 3.
So, x (- ∞, 3).

18. 5x – 3 > 3x – 5
18. Given, 5x – 3 > 3x 5
5x –3x≥ –5 + 3.
2x ≥ –2.
x
x ≥ –1.
So, x [1, - ∞ ).

19. 3 (1 – x) < 2 (x + 4)
19. Given, 3 (1–x) < 2 (x + 4)
3 –3x < 2x + 8
3–8 < 2x+ 3x
–5 < 5x
-1< x
So, x ∈ (–1, ∞ )

22. To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
22. Let ‘x’ be the marks obtained by Sunita in the 5th exam.
Then, average marks ≥ 90.
.
368 + x ≥ 90 × 5.
368 + x ≥ 450.
x ≥ 450 - 368.
x ≥ 82.
Minimum mark required= 82.
23. Find all pairs of consecutive odd positive integers both of which are smaller than10 such that their sum is more than 11.
23. Let x be the smaller of the consecutive odd positive integers, then the. other is x + 2 {Since the consecutive odd number are differ by 2.}
then the. other is x + 2
so, x < 10 and x + 2 < 10 x< 8
and x + (x + 2) > 11.
2x > 11 - 2
2x > 9
and hence,
4.5 As x ∈ z, x = 5 and x = 7 and x is odd The reqd. possible pairs by (x, x + 2) are (5, 7), (7, 9).
25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
25. Let x cm be the shortest side of the triangle.
Thus, the other 2 sides are “3x” cm and “3x - 2” cm
Given, perimeter of A triangle ≥ 61
x + 3x - 3x- 2 ≥ 61
7x - 21 ≥ 61
7x ≥ 61 + 21
x ≥ 9.
The minimum length of the shortest side is 9 cm.
Class 11 Math Linear Inequalities Ex 6.2 Solutions
Solve the following inequalities graphically in a two-dimensional plane:
27. x + y < 5
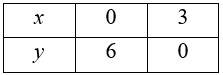
27. For inequality, x+y < 5, the equation of line is x+y = 5.
We consider the tableto plot x+y=5.
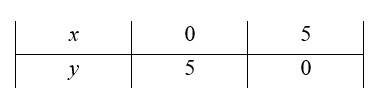
Graph of x+y = 5 is given as dotted line in fig 1. This lines divides by plane in two half planes I and II. We select a point not on the line, say (0,0) which lies in region I.
Since, 0+0 < 5
0 < 5 is true.
The solution region is I. (where origin (0,0) is included)
The dotted line indicates that any point on the line does not satisfy the given inequality.
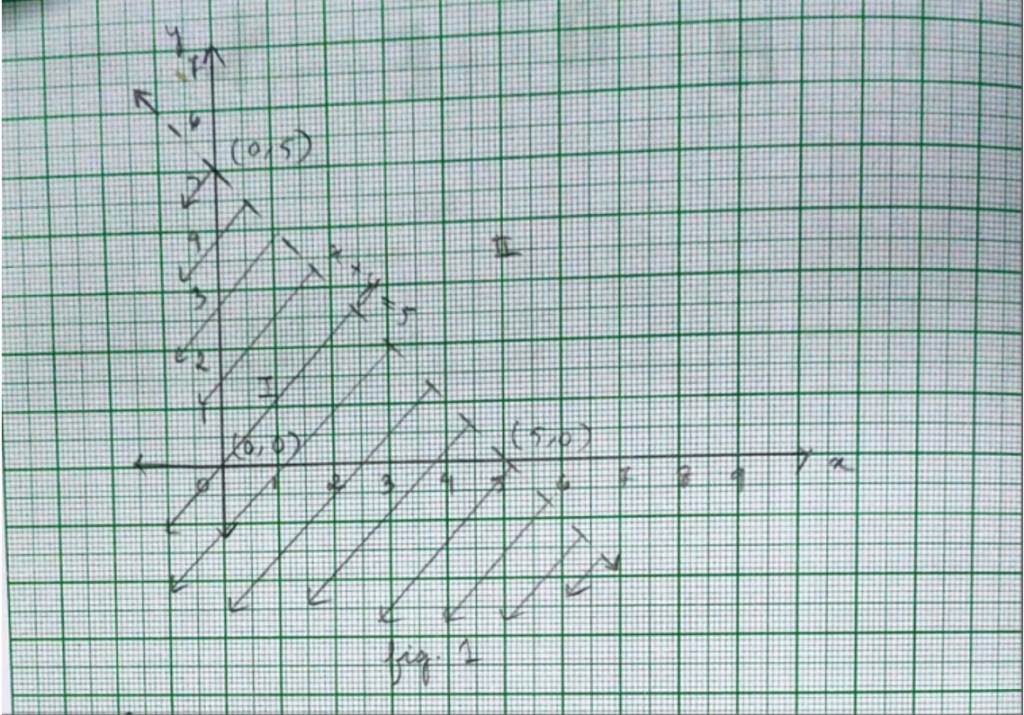
31. x – y ≤ 2
31. For the inequality x – y≤ 2 so the equation of line is x – y=2. We consider the table below to plat x – y=2
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.
0 – 0 ≤ 2
0 ≤ 2 which is true.
So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any point on the line also satisfy the given inequality.
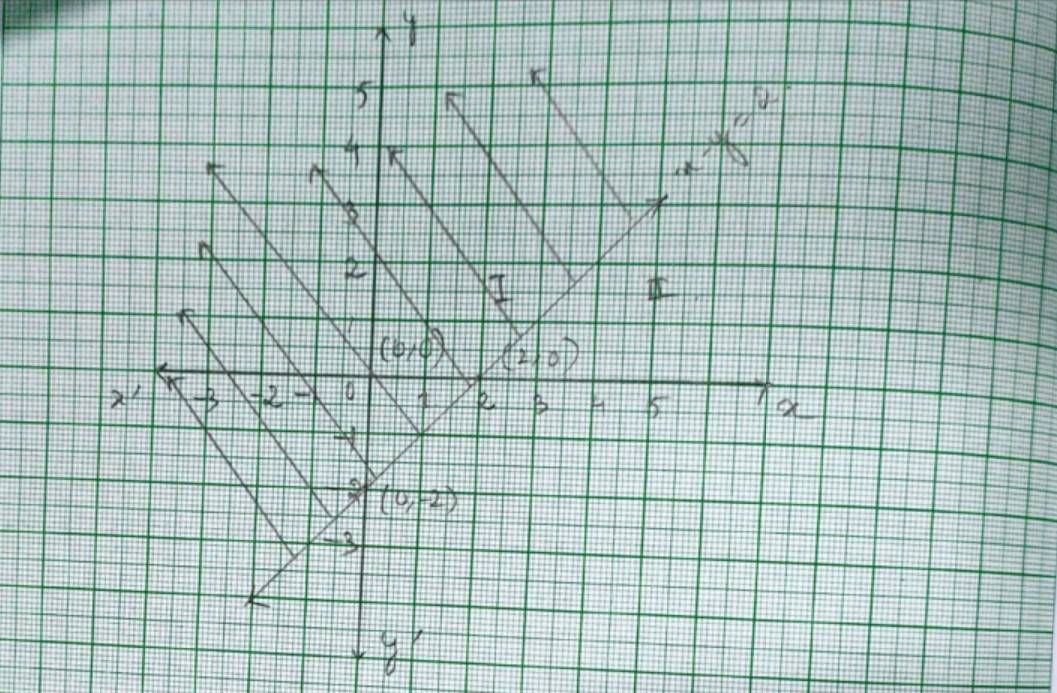
32. 2x – 3y > 6
32. For the inequality, 2x – 3y>6 the eqn is 2x – 3y=6. We consider the table below to plot 2x – 3y=6.
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.
2 × 0 – 3 × 0>6
0>6 which is false.
So, the solution region is II which does not includes the origin (0,0).
The dotted line indicates that the any point on the line does not satisfy the given inequality.
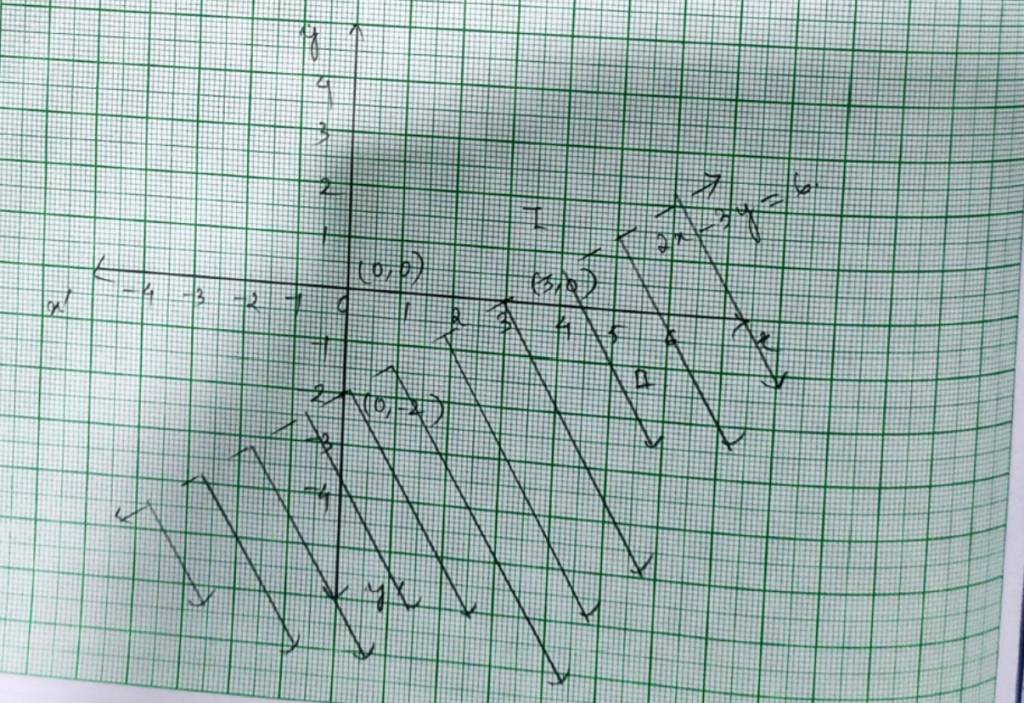
33. – 3x + 2y ≥– 6
33.For the inequality –3x+2y≥ –6 the equation of line is – 3x+2y=6.
We consider the table below to plot – 3x+2y= –6.
This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality,
–3 × 0+2 × 0 ≥ –6
0 ≥ –6 which is true.
So, the solution region is I which includes the origin. The continuous line also indicates that any point on the line also satisfy the given inequality.
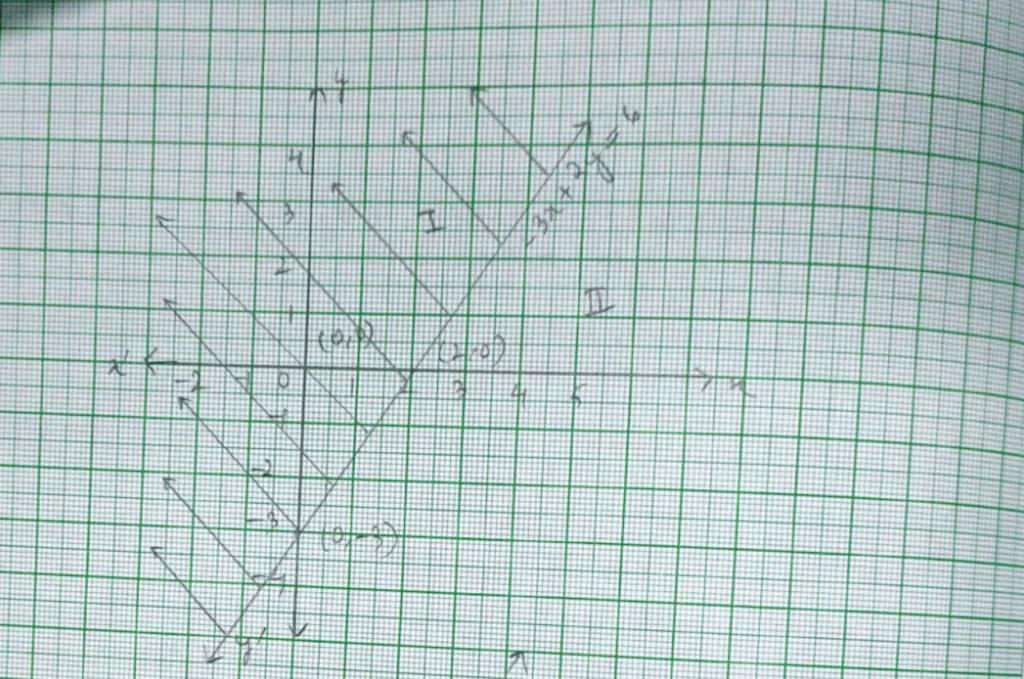
34. 3y – 5x < 30
34. For the inequality 3y – 5x<30, the equation of line is 3y – 5x=30. We consider the table below to plot 3y – 5x =30.
This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality.
3 × 0 – 5 × 0 < 30
0 < 30 which is true.
So, the solution region is I which includes the origin. The dotted line indicates that any point on the line will not satisfy the given inequality.
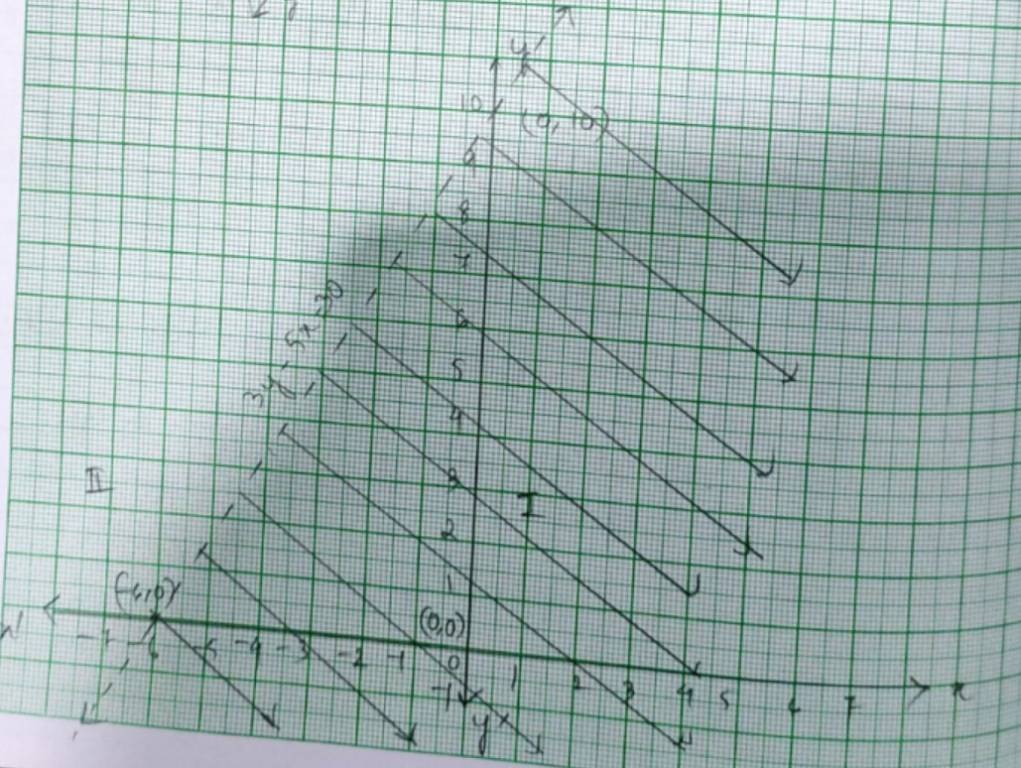
35. y < – 2
35. For the given equation inequality y< –2, the equation of line is y= –2
This line devides the xy-plane into two planer I and II. We take a point (0,0) to check the correctness of the inequality.
So, 0< –2
0< –2 which is false.
So, the solution of the region is II which does not include the origin.
The dotted line indicates that any point on the line does not satisfy the inequality.
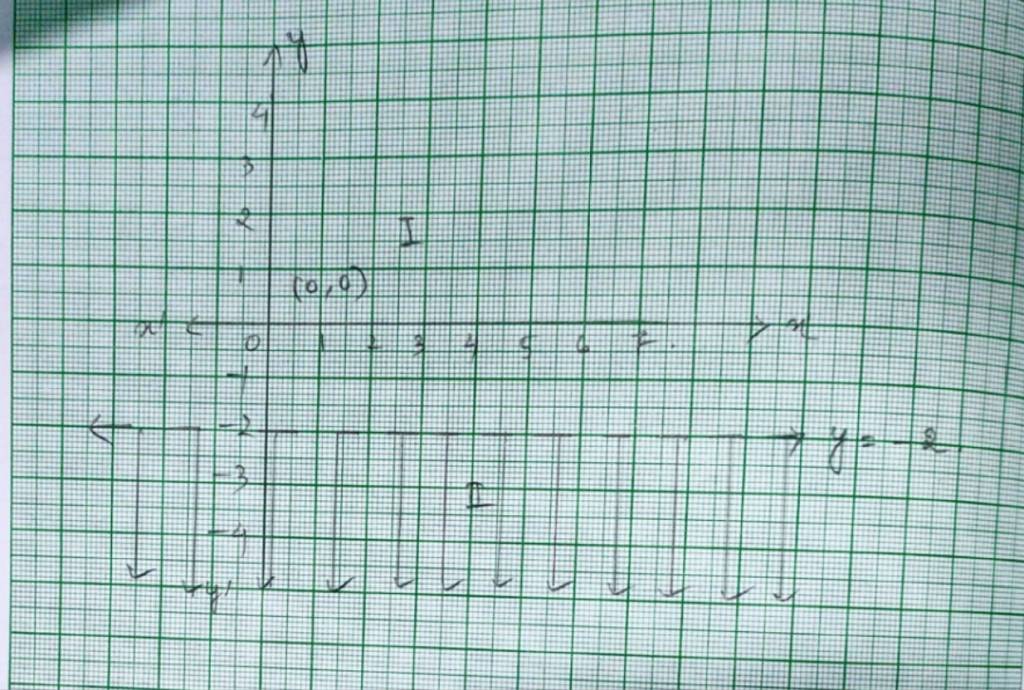
36. x > – 3
36. For the given inequality, x> –3.
The equation of the line is x= –3.
This line divides the xy-plane into planer I and II. We take a point (0,0) to check the correctness of the inequality.
So, 0> –3 which is true.
So, the solution of the region is I which includes the origin.
The dotted line indicates that any point on the line does not satisfy the inequality.

Class 11 Chapter 6 Linear Inequalities Exercise 6.3 Solutions
38. 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
38.
2. The given system of inequalities are
3x+2y≤ 12- (1)
x≥ 1- (2)
y≥ 2- (3)
We draws the graphs of the lines 3x+2y=12 using points and as 3 × 0 + 2 × 0 ≤ 12
The solution is plane which includes the origin (0, 0).
0 ≤ 12
and x = 1 and y = 2.
The inequality (1), (2) and (3) represents the region between these three lines including the points on the respective lines. So, every point on the shaded region in first quadrant represents a solution of the given system of inequalities.
40. x + y ≥ 4, 2x – y < 0
40. The given system of inequalities is
x + y ≥ 4.- (1)
2x – y< 0.- (2)
The corresponding equations are x+y=4 and 2x – y=0.
x | 0 | 4 |
y | 4 | 0 |
and
X | 0 | 1 |
Y | 0 | 2 |
Put (x, y)= (1,1) in (1) and (2).
So, 1+1 ≥ 4
2 ≥ 4 which is not true.
and 2 × 1 – 1<0
1<0 which is not true.
So solution of plane of inequality (1) and (2) does not include the plane with point (1,1).
? The reqd. solution of the given system of inequality is the shaded portion.
42. x + y ≤ 6, x + y ≥ 4
42. The given system of inequality is
x+y≤ 6 - (1)
x+y≥ 4- (2)
So the corresponding equations are
x+y=6
x | 0 | 6 |
y | 6 | 0 |
and x + y = 4
x | 4 | 0 |
y | 0 | 4 |
Putting (x, y)= (0,0) in equality (1) and (2),
0+0 ≤ 6 and 0 + 0 ≥ 4
0 ≤ 6 is true. => 0 ≥ 4 is false.
So, solution of plane of inequality (1) includes the origin and inequality (2) does not includes the origin.
? The reqd solution of the given system of inequality is the shaded region.
43. 2x + y ≥ 8, x + 2y ≥ 10
43. Given system of inequality is
2x+y≥ 8- (1)
x+2y≥ 10- (2)
The corresponding equations are
2x + y = 8
x | 0 | 4 |
y | 8 | 0 |
and x + 2y = 10
x | 10 | 0 |
y | 0 | 5 |
Now, putting (x, y)= (0,0) in inequality (1) and (2),
2 × 0+8 ≥ 8
0 ≥ 8 which is not true.
and 0+2 × 0 ≥ 10
0 ≥ 10 which is not true.
So, solution of plane of inequality (1) and (2) does not include the origin (0,0)
? The required solution of the given system of inequality is the shaded region.

44. x + y ≤ 9, y >x, x ≥ 0
44. The given system of inequality is
x+y≤ 9- (1)
y>x- (2)
x≥ 0 - (3)
The corresponding equation of (1) is x+y=9 and (2) is y=x
x | 9 | 0 |
y | 0 | 9 |
x | 0 | 1 |
y | 0 | 1 |
Substituting (x, y)= (0,0) in (1),
0+0 ≤ 9 => 0 ≤ 9 which is true.
And putting (1,0) in (2)
0> 1which is false.
So, solution region of inequality (1) includes origin (0,0) and solution region of inequality (2) excludes plane having (1,0).
? Solution of region of given system of inequality is the shaded region.

45. 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
45. The given system of inequality is
5x+4y≤ 20 - (1)
x≥ 1 - (2)
and y≥ 2 - (3)
The equation of inequality (1) is 5x+4y=20.
x | 4 | 0 |
y | 0 | 5 |
Putting (x, y)= (0,0) in inequality (1) we get,
5 × 0+4 × 0 ≤ 20 => 0 ≤ 20 which is true.
So, the solution region of inequality (1) includes the plane with origin (0,0).
∴ The shaded region indicates the solution of the given system of inequality.
46. 3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0
46. The given system of inequality is
3x+4y ≤ 60 - (1)
x+3y ≤ 30- (2)
x≥ 0 - (3)
xy≥ 0 - (4)
The corresponding equation of (1) and (2) are
3x + 4y = 60
x | 20 | 0 |
y | 0 | 15 |
and x + 3y = 30
x | 0 | 30 |
y | 10 | 0 |
Putting (x, y)= (0,0) in equality (1) and (2),
3 × 0+4 × 0 ≤ 60 and 0+3 × 0 ≤ 30
0 ≤ 60 which is true and 0 ≤ 30 which is true
So, the solution plane of inequality (1) and (2) is the plane including origin (0,0)
∴ The shaded portion is the solution of the given system of inequality.
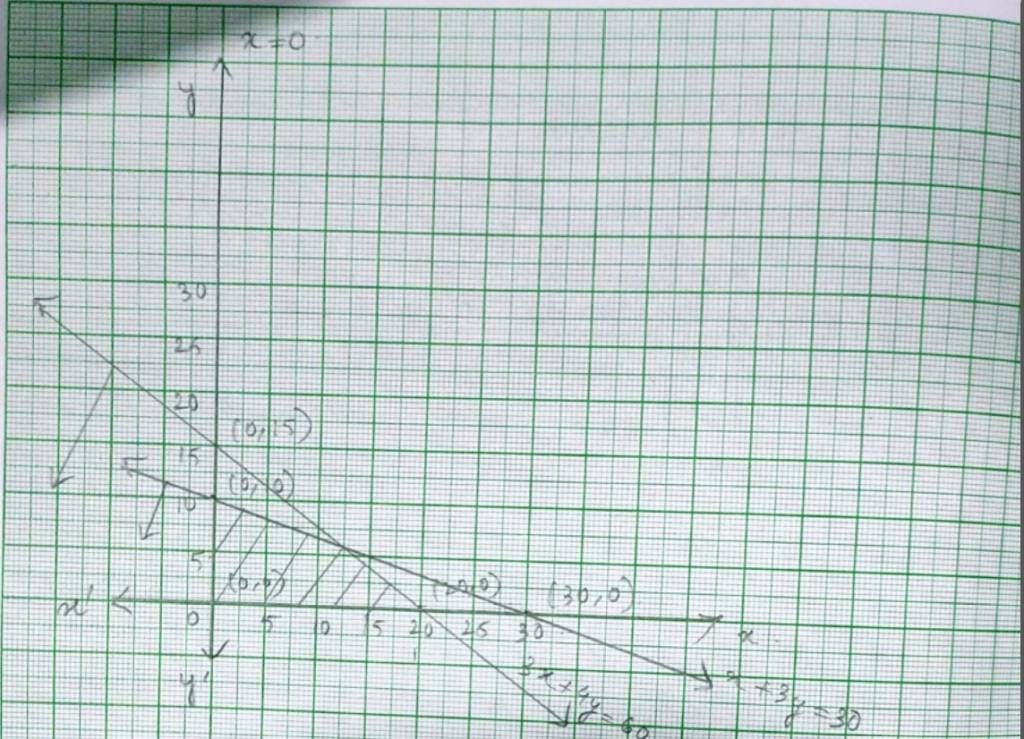
47. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
47. The given system of inequality is
2x + y ≥ 4- (1)
x + y ≤ 3- (2)
2x – 3y ≤ 6- (3)
The corresponding equation are
2x + y = 4
x | 2 | 0 |
y | 0 | 4 |
and x + y = 3
x | 0 | 3 |
y | 3 | 0 |
and 2x + 3y = 6
x | 3 | 0 |
y | 0 | –2 |
Putting (x, y)= (0,0) in (1), (2) and (3),
2 × 0+0 ≥ 4
0 ≥ 4 which is false.
and 0+0 ≤ 3 => 0 ≤ 3 which is true.
and 2 × 0 – 3 × 0 ≤ 6 => 0 ≤ 6which is also true.
So, solution of inequality (1) excludes plane with origin while solution of inequality (2) and (3) includes the plane with origin.

49. 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
49. The given system of inequality is
4x+3y≤ 60- (1)
y≥ 2x- (2)
x≥ 3- (3)
andx, y ≥ 0- (4)
The corresponding equation of inequality (1) and (2) are
4x+3y= 60
x | 0 | 15 |
y | 20 | 0 |
and y = 2x
x | 0 | 1 | 2 |
y | 0 | 2 | 4 |
Putting (1,0) in inequality (1) and (2) we get,
4 × 1+3 × 0 ≤ 60
4 ≤ 60 which is true.
and 0 ≥ 2 × 1
0 ≥ 2 which is false.
So, solution of inequality (1) includes the plane with point (1,0) whereas the solution of inequality (2) excludes the plane with point (1,0).
? The shaded region is the solution of the given system of inequality.

51. x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
51. The given system of inequality is
x+2y≤ 10- (1)
x+y≥ 1 - (2)
x – y ≤ 0 - (3)
x≥ 0 and y≥ 0 - (4)
The corresponding equation of (1), (2) and (3) are
x + 2y = 10
x | 0 | 10 |
y | 5 | 0 |
and x + y =1
x | 0 | 1 |
y | 1 | 0 |
and x – y = 0
x | 0 | 1 |
y | 0 | 1 |
Putting (2,0)= (x, y) in inequality (1), (2) and (3),
2+2 × 0 ≤ 10 => 2≤ 10 is true.
and 2+0 ≥ 1 => 2 ≥ 1 is true.
and 2 – 0 ≤ 0 => 2 ≤ 0 is false.
So, the solution of inequality (1) and (2) is the plane that includes point (2,0) whereas the solution of inequality (3) is the plane which includes point (2, 0)
∴ The shaded region represents the solution of the given system of inequality.
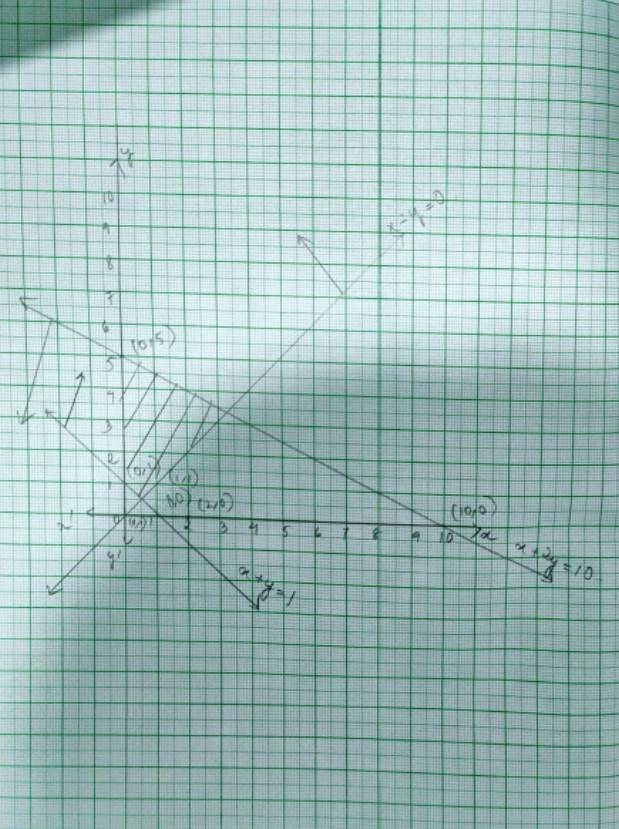
62. A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by
62. It is given that
Putting we get,
(Subtracting 32 throughout)
Multiplying by throughout,
Hence, the required range of temperature is between
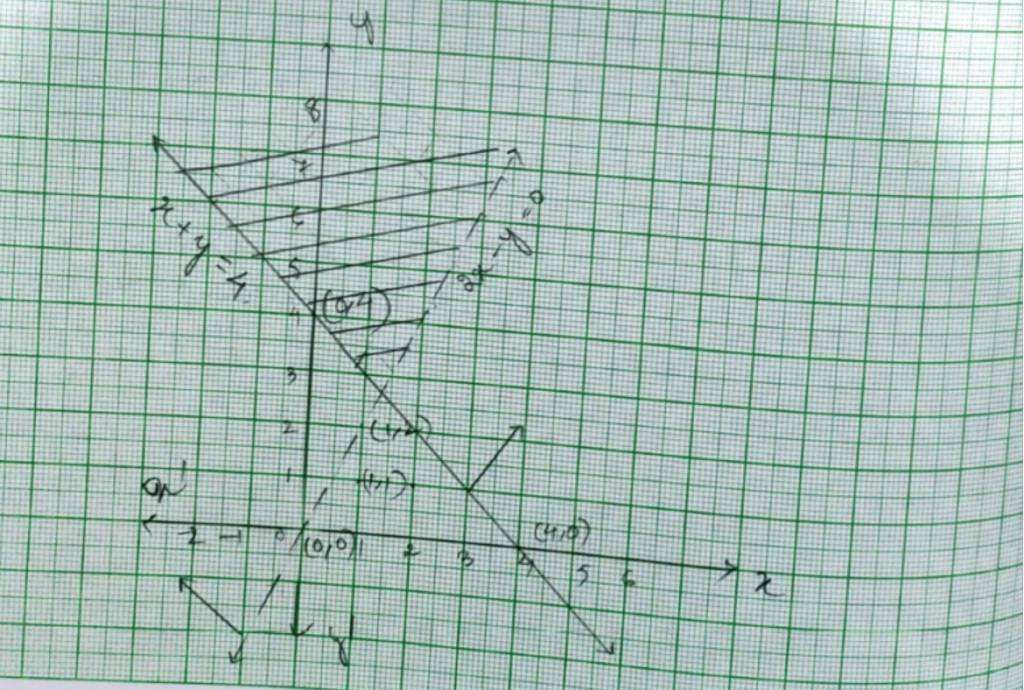
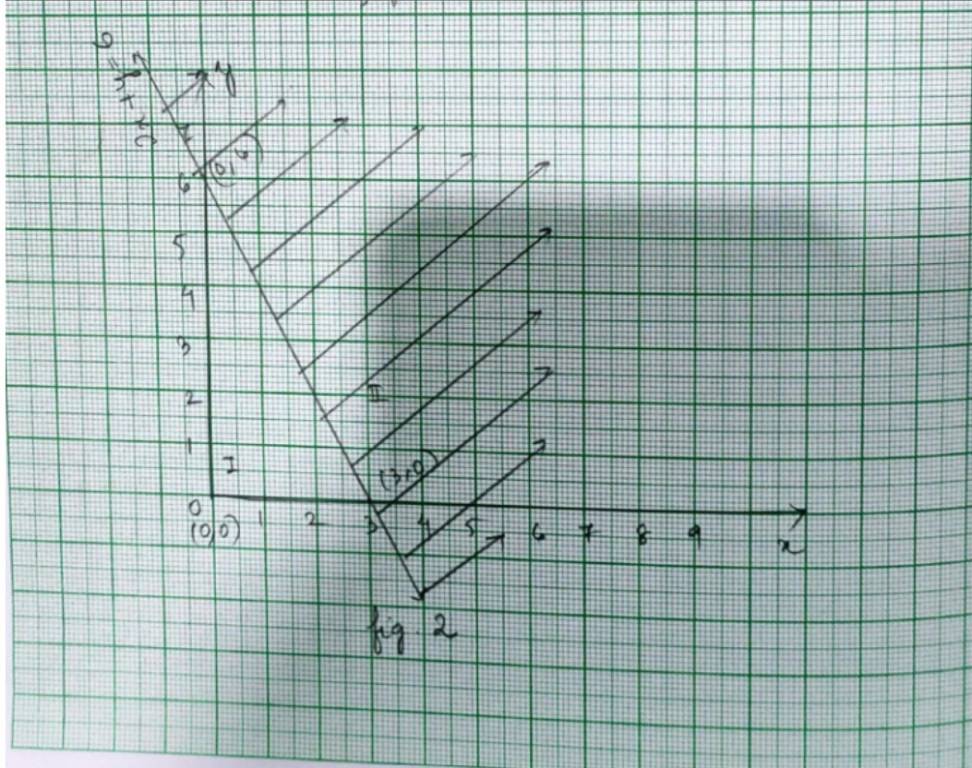
28. Kindly Consider the following 2x + y ≥ 6
28. For inequality, 2x+y≥ 6, the equation of line is 2x+y=6.
We consider the table below to pot 2x+y=6.
Graph of 2x+y=6 is given as a continuous line in fig 2.
This line divides xy-plane in two half planes I and II.
We select 0 (0,0) and check the correctness of the inequality.
is 2 × 0+0 ≥ 6.
0 ≥ 6 which is false.
So, the solution region is II where origin (0,0) is included.
The continuous line indicates that any point on the line. also satisfy the given inequality.
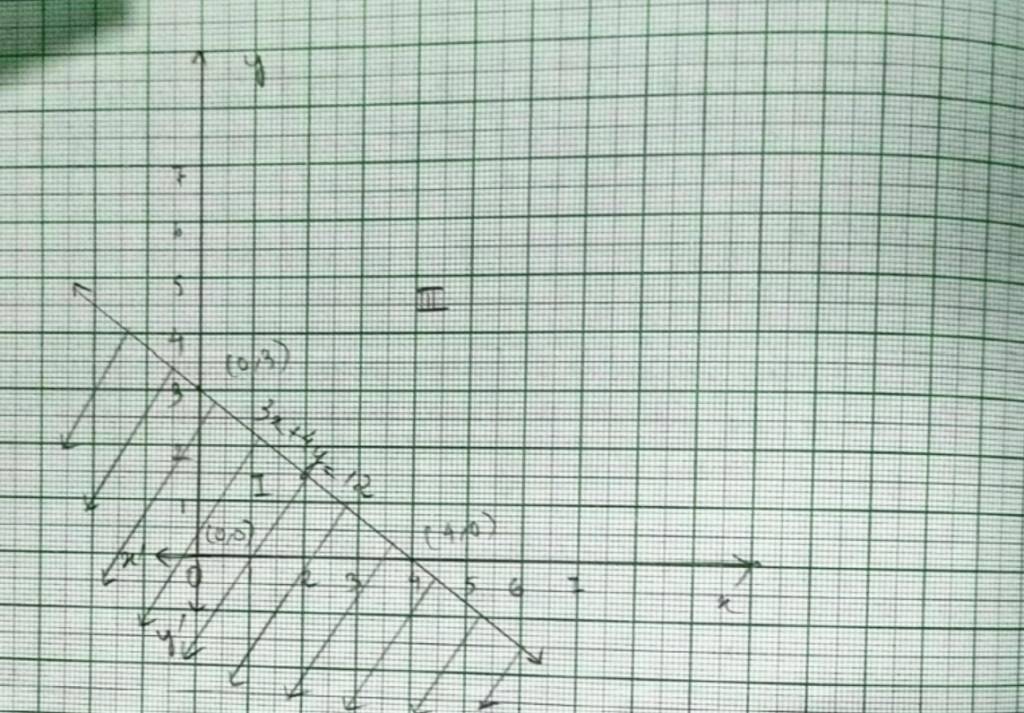
29. Kindly consider the following 3x + 4y ≤ 12
29. For inequality 3x+4y≥ 12 the equation of the line is 3x+4y=12
We consider the table below to plot 3x+4y=12.
This line devides the xy-plane into half planer I and II.
We select point 0 (0,0) and check the correctness of the inequality.
i.e., 3 × 0+4 × 0 ≤ 12.
0+0 ≤ 12
0 ≤12 which is true.
So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any points in the line also satisfy the given inequality.
30. Kindly consider the following y + 8 ≥ 2x
30.
30. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.
The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality.
i.e., 0+8 ≤ 2 × 0
0 ≤ 0 which is true.
So, the solution region is I which includes the rigin (0,0). The continuous line also indicates that any points on the line also satisfy the given inequality.
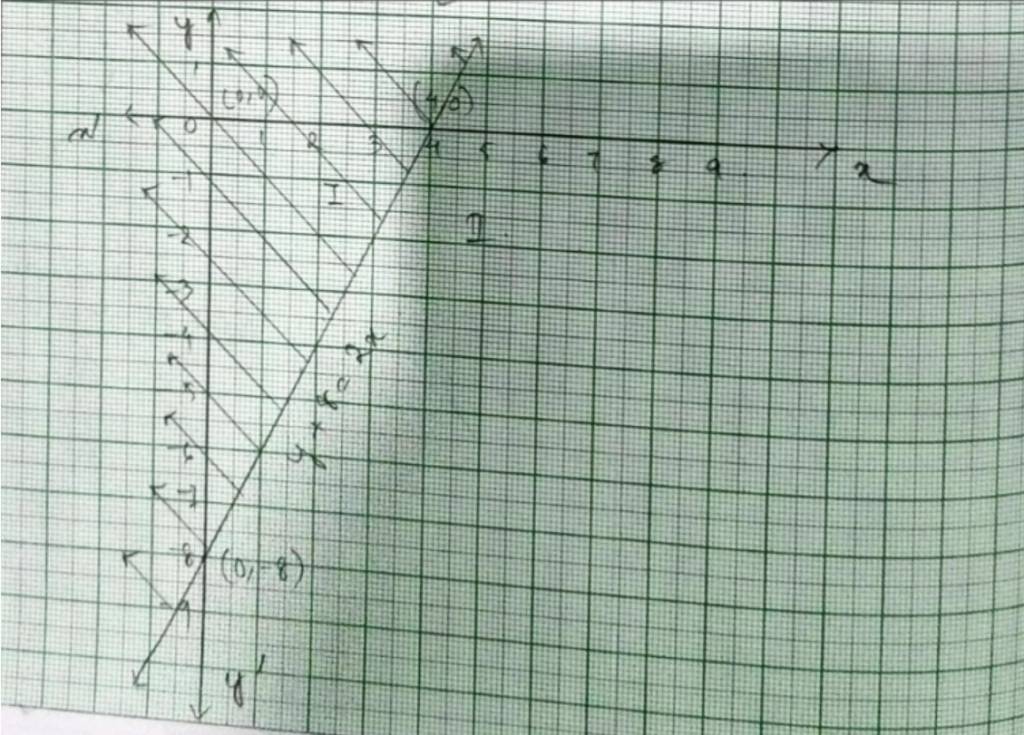
Class 11 Math Linear Inequalities Exercise 6.2 NCERT Solutions (Old NCERT)
Linear Equation Ex 6.2 focuses on linear inequalities with two variables, solution methods, and representing their solutions graphically. Exercise 6.2 of Linear equalities helps aspirants understand that inequalities often have an infinite number of solutions that can be represented as a shaded region on a coordinate plane. Linear Inequalities Exercise 6.2 consists of 10 questions. Candidates can find the complete solution below;
Class 11 Math Linear Inequalities EX 6.2 SolutionsSolve the following inequalities graphically in a two-dimensional plane: Q1. x + y < 5 |
| A.1. For inequality, x+y <5, the equation of line is x+y=5. We consider the tableto plot x+y=5.
Graph of x+y=5 is given as dotted line in fig 1. This lines divides by plane in two half planes I and II. We select a point not on the line, say (0,0) which lies in region I. Since, 0+0<5 0<5is true. The solution region is I. (where origin (0,0) is included) The dotted line indicates that any point on the line does not satisfy the given inequality.
|
| Q2. 2x + y ≥ 6 |
| A.2. For inequality, 2x+y≥ 6, the equation of line is 2x+y=6. We consider the table below to pot 2x+y=6.
Graph of 2x+y=6 is given as a continuous line in fig 2. This line divides xy-plane in two half planes I and II. We select 0(0,0) and check the correctness of the inequality. is 2 × 0+0 ≥ 6. 0 ≥ 6 which is false. So, the solution region is II where origin (0,0) is included. The continuous line indicates that any point on the line. also satisfy the given inequality.
|
| Q3. 3x + 4y ≤ 12 |
| A.3. For inequality 3x+4y≥ 12 the equation of the line is 3x+4y=12 We consider the table below to plot 3x+4y=12.
This line devides the xy-plane into half planer I and II. We select point 0(0,0) and check the correctness of the inequality. i.e., 3 × 0+4 × 0 ≤ 12. 0+0 ≤ 12 0 ≤12 which is true. So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any points in the line also satisfy the given inequality.
|
| Q4. y + 8 ≥ 2x |
| A.4. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.
The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality. i.e., 0+8 ≤ 2 × 0 0 ≤ 0 which is true. So, the solution region is I which includes the rigin (0,0). The continuous line also indicates that any points on the line also satisfy the given inequality.
|
| Q5. x – y ≤ 2 |
| A.5. For the inequality x – y≤ 2 so the equation of line is x – y=2. We consider the table below to plat x – y=2
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality. 0 – 0 ≤ 2 0 ≤ 2 which is true. So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any point on the line also satisfy the given inequality. |
| Q6. 2x – 3y > 6 |
| A.6. For the inequality, 2x – 3y>6 the eqn is 2x – 3y=6. We consider the table below to plot 2x – 3y=6.
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality. 2 × 0 – 3 × 0>6 0>6 which is false. So, the solution region is II which does not includes the origin (0,0). The dotted line indicates that the any point on the line does not satisfy the given inequality.
|
| Q7. – 3x + 2y ≥– 6 |
| A.7. For the inequality –3x+2y≥ –6 the equation of line is – 3x+2y=6. We consider the table below to plot – 3x+2y= –6.
This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality, –3 × 0+2 × 0 ≥ –6 0 ≥ –6 which is true. So, the solution region is I which includes the origin. The continuous line also indicates that any point on the line also satisfy the given inequality.
|
| Q8. 3y – 5x < 30 |
| A.8. For the inequality 3y – 5x<30, the equation of line is 3y – 5x=30. We consider the table below to plot 3y – 5x =30.
This line divides the xy-plane into two planer I and II. We select a point (0,0) and check the correctness the inequality. 3 × 0 – 5 × 0<30 0<30 which is true. So, the solution region is I which includes the origin. The dotted line indicates that any point on the line will not satisfy the given inequality.
|
| Q9. y < – 2 |
| A.9. For the given equation inequality y< –2, the equation of line is y= –2 This line devides the xy-plane into two planer I and II. We take a point (0,0) to check the correctness of the inequality. So, 0< –2 0< –2 which is false. So, the solution of the region is II which does not include the origin. The dotted line indicates that any point on the line does not satisfy the inequality.
|
| Q10. x > – 3 |
| A.10. For the given inequality, x> –3. the equation of the line is x= –3. This line divides the xy-plane into planer I and II. We take a point (0,0) to check the correctness of the inequality. So, 0> –3 which is true. So, the solution of the region is I which includes the origin. The dotted line indicates that any point on the line does not satisfy the inequality.
|
Class 11 Math Linear Inequalities Exercise 6.3 NCERT Solutions (OLD NCERT)
Linear Inequalities Exercise 6.3 focuses on the graphical representation of systems of linear inequalities in two variables. The concepts used in this exercise are widely used in linear programming, optimization problems, and real-world applications like business decision-making, resource allocation, and economic analysis. Exercise 6.3 consists of 15 questions, all the solutions are given below.
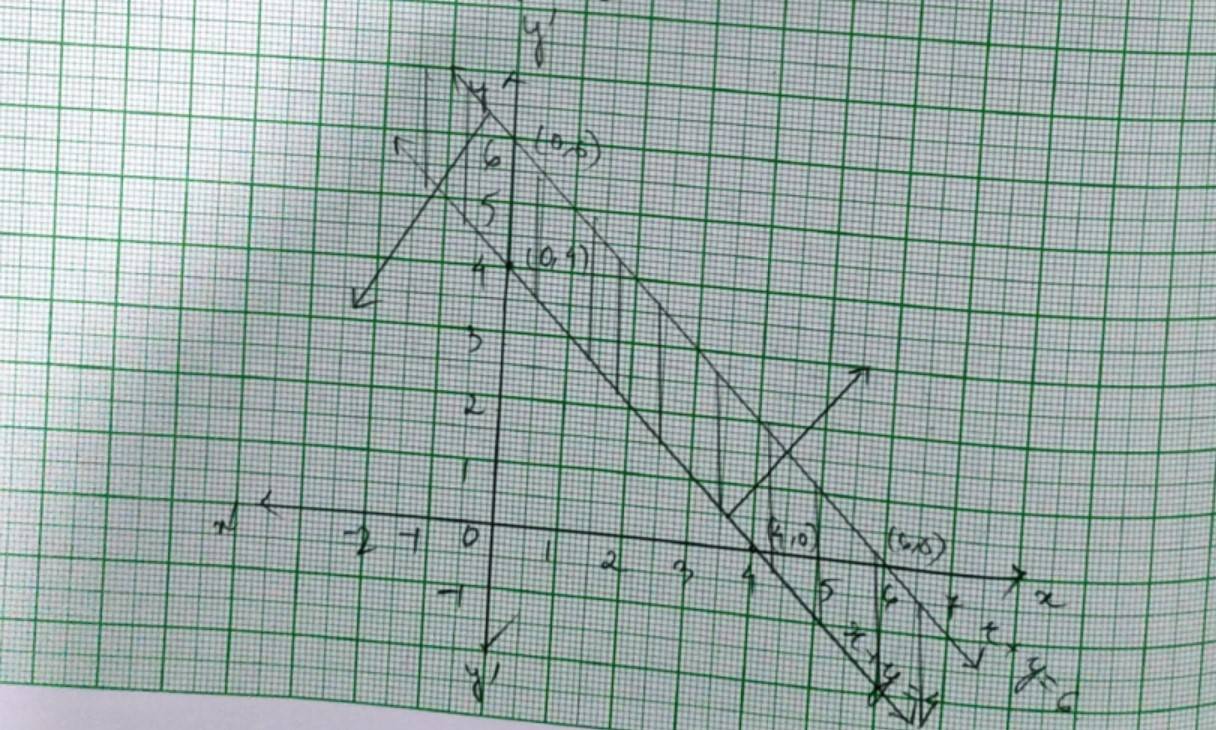
Class 11 Chapter 6 Linear Inequalities Exercise 6.3 SolutionsQ1. x ≥ 3, y ≥ 2 |
| Q2. 3x + 2y ≤ 12, x ≥ 1, y ≥ 2 |
| A.2. The given system of inequalities are 3x+2y≤ 12----------(1) x≥ 1----------(2) y≥ 2----------(3) We draws the graphs of the lines 3x+2y=12 using points and as 3 × 0 + 2 × 0 ≤ 12 The solution is plane which includes the origin (0, 0). 0 ≤ 12
and x = 1 and y = 2. The inequality (1), (2) and (3) represents the region between these three lines including the points on the respective lines. So, every point on the shaded region in first quadrant represents a solution of the given system of inequalities. |
| Q3. 2x + y ≥ 6, 3x + 4y < 12 |
| A.3.The given system of inequalities is 2x+y≥ 6 ----------------------(1) 3x+4y≤ 12---------------------(2) The corresponding equations are 2x + y = 6 |
| Q4. x + y ≥ 4, 2x – y < 0 | ||||||||||||
| A.4. The given system of inequalities is x + y ≥ 4.---------------------(1) 2x – y< 0.---------------------(2) The corresponding equations are x+y=4 and 2x – y=0.
and
Put (x, y)=(1,1) in (1) and (2). So, 1+1 ≥ 4 2 ≥ 4 which is not true. and 2 × 1 – 1<0 1<0 which is not true. So solution of plane of inequality (1) and (2) does not include the plane with point (1,1). ⸫ The reqd. solution of the given system of inequality is the shaded portion.
|
| Q5. 2x – y >1, x – 2y < – 1 | ||||||||||||
| A.5.The given system of inequality is 2x – y> 1 -----------------(1) x – 2y< –1-----------------(1) So the corresponding equations are 2x – y=1
and x – 2y= –1
Putting (x, y)=(0,0) in (1) and (2) to cheek the inequality 2 × 0 – 0 > 1 0 > 1 which is not true. and 0 – 2 × 0< –1 0< –1 which is not true. So, the solution of plane of inequality (1)and (2) does not include the plane with point (0,0) or origin. ⸫ The reqd. solution of the given system of inequality is the shaded region. |
| Q6. x + y ≤ 6, x + y ≥ 4 | ||||||||||||
| A.6. The given system of inequality is x+y≤ 6 ---------------(1) x+y≥ 4---------------(2) So the corresponding equations are x+y=6
andx + y = 4
Putting (x, y)=(0,0) in equality (1) and (2), 0+0 ≤ 6 and 0 + 0 ≥ 4 0 ≤ 6 is true. => 0 ≥ 4 is false. So, solution of plane of inequality (1) includes the origin and inequality(2) does not includes the origin. ⸫The reqd solution of the given system of inequality is the shaded region.
|
| Q7. 2x + y ≥ 8, x + 2y ≥ 10 | ||||||||||||
| A.7. Given system of inequality is 2x+y≥ 8-----------------(1) x+2y≥ 10-----------------(2) The corresponding equations are 2x + y = 8
and x + 2y = 10
Now, putting (x, y)=(0,0) in inequality (1) and (2), 2 × 0+8 ≥ 8 0 ≥ 8 which is not true. and 0+2 × 0 ≥ 10 0 ≥ 10 which is not true. So, solution of plane of inequality (1) and (2) does not include the origin (0,0) ⸫The required solution of the given system of inequality is the shaded region.
|
| Q8. x + y ≤ 9, y >x, x ≥ 0 | ||||||||||||
| A.8.The given system of inequality is x+y≤ 9-------------------(1) y>x-------------------(2) x≥ 0 -------------------(3) The corresponding equation of (1) is x+y=9 and (2) is y=x
Substituting (x, y)=(0,0) in (1), 0+0 ≤ 9 => 0 ≤ 9 which is true. And putting (1,0) in (2) 0> 1which is false. So, solution region of inequality (1) includes origin (0,0) and solution region of inequality (2) excludes plane having (1,0). ⸫Solution of region of given system of inequality is the shaded region.
|
| Q9. 5x + 4y ≤ 20, x ≥ 1, y ≥ 2 | ||||||
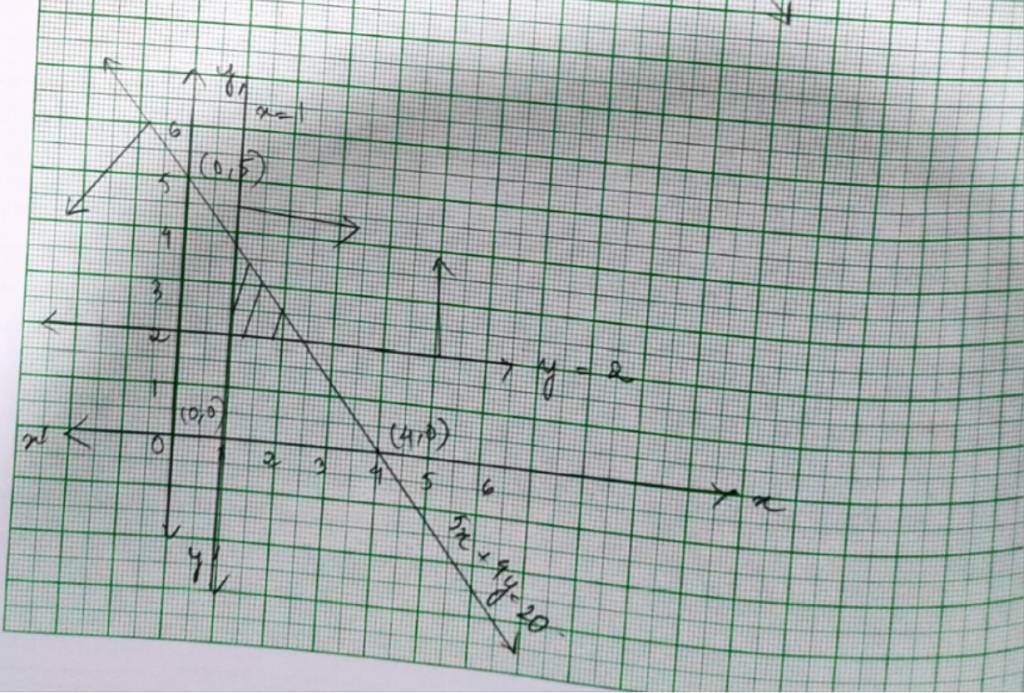
| A.9. The given system of inequality is 5x+4y≤ 20 -----------------------(1) x≥ 1 -----------------------(2) and y≥ 2 -----------------------(3) The equation of inequality (1) is 5x+4y=20.
Putting (x, y)=(0,0) in inequality (1) we get, 5 × 0+4 × 0 ≤ 20 => 0 ≤ 20 which is true. So, the solution region of inequality (1) includes the plane with origin (0,0). ⸫The shaded region indicates the solution of the given system of inequality.
|
| Q10. 3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0 | ||||||||||||
| A.10. The given system of inequality is 3x+4y ≤ 60 -------------------(1) x+3y ≤ 30-------------------(2) x≥ 0 -------------------(3) xy≥ 0 -------------------(4) The corresponding equation of (1) and (2) are 3x + 4y = 60
and x + 3y = 30
Putting (x, y)=(0,0) in equality (1) and (2), 3 × 0+4 × 0 ≤ 60 and 0+3 × 0 ≤ 30 0 ≤ 60 which is true and 0 ≤ 30 which is true So, the solution plane of inequality (1) and (2) is the plane including origin (0,0) ⸫The shaded portion is the solution of the given system of inequality.
|
| Q11. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6 | ||||||||||||||||||
| A.11.The given system of inequality is 2x + y ≥ 4---------(1) x + y ≤ 3---------(2) 2x – 3y ≤ 6---------(3) The corresponding equation are 2x + y = 4
and x + y = 3
and 2x + 3y = 6
Putting (x,y)=(0,0) in (1), (2) and (3), 2 × 0+0 ≥ 4 0 ≥ 4 which is false. and 0+0 ≤ 3 => 0 ≤ 3 which is true. and 2 × 0 – 3 × 0 ≤ 6 => 0 ≤ 6which is also true. So, solution of inequality (1) excludes plane with origin while solution of inequality (2) and (3) includes the plane with origin.
⸫The shaded portion is the reqd. solution of the given system of inequality. |
| Q12. x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0 ,y ≥ 1 | ||||||||||||
| A.12. The given system of inequality is x – 2y≤ 3 ------------(1) 3x – 4y≥12------------(2) x ≥ 0 ------------(3) y≥ 1 ------------(4) The corresponding equation of (1) and (2) are x – 2y= 3
and 3x – 4y=12
Putting (x, y)=(0,0) in inequality (1) and (2), 0 – 2 × 0 ≤ 3 => 0 ≤ 3 is true. and 3 × 0+4 × 0 ≥ 12 => 0 ≥ 12 is false. So, solution of inequality (1) includes plane wilt origin (0,0) while solution plane of inequality (2) includes the origin. ⸫The shaded portion determines the solution region of the given system of inequality.
|
| Q13. 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0 | ||||||||||||||
| A.13. The given system of inequality is 4x+3y≤ 60-----------(1) y≥ 2x------------(2) x≥ 3------------(3) andx, y ≥ 0------------(4) The corresponding equation of inequality (1) and (2) are 4x+3y= 60
and y = 2x
Putting (1,0) in inequality (1) and (2) we get, 4 × 1+3 × 0 ≤ 60 4 ≤ 60 which is true. and 0 ≥ 2 × 1 0 ≥ 2 which is false. So, solution of inequality (1) includes the plane with point (1,0) whereas the solution of inequality (2) excludes the plane with point (1,0). ⸫The shaded region is the solution of the given system of inequality.
|
| Q14. 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0 | ||||||||||||
| A.14.The given system of inequality is 3x+2y≤ 150-------------(1) x+4y≤ 80-------------(2) x≤ 15 -------------(3) y≥ 0 and x≥ 0 -------------(4) The corresponding equation of (1) and (2) are 3x + 2y = 150
and x + 4y =80
Putting (0,0)=(x, y) in inequality (1) and (2) we get, 3 × 0+2 × 0 ≤ 150 => 0 ≤ 150 is true. and 0+4 × 0 ≤ 80 => 0 ≤ 80 is true. So, the solution plane of both inequality (1) and (2) includes the origin (0,0). ⸫The shaded region is the solution of the given system of inequality.\
|
| Q15. x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0 | ||||||||||||||||||
| A.15. The given system of inequality is x+2y≤ 10-------------(1) x+y≥ 1 -------------(2) x – y ≤ 0 -------------(3) x≥ 0 and y≥ 0 -------------(4) The corresponding equation of (1), (2) and (3) are x + 2y = 10
and x + y =1
and x – y = 0
Putting (2,0)=(x, y) in inequality (1), (2) and(3), 2+2 × 0 ≤ 10 => 2≤ 10 is true. and 2+0 ≥ 1 => 2 ≥ 1 is true. and 2 – 0 ≤ 0 => 2 ≤ 0 is false. So, the solution of inequality (1) and (2) is the plane that includes point (2,0) whereas the solution of inequality (3) is the plane which includes point (2, 0) ⸫The shaded region represents the solution of the given system of inequality. |
Class 11 Math Linear Inequalities Miscellaneous Exercise Solution(Old NCERT)
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
- Relations and Functions
- Sets
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test