
NCERT Solutions for Class 11 Maths Chapter 1 – Sets is an important chapter for Class 11 students as it is used in almost every branch of Mathematics. It defines the concepts of relations and functions. Moreover, the study of sequences, geometry, and probability requires an understanding of set concepts.
Class 11 Maths Chapter 1 Solutions lays the foundation of many advanced concepts of Mathematics. The following topics are covered in detail in this chapter: Venn diagrams, Finite and Infinite Sets, Sets and Their Representations, Universal Set, The Empty Set, Operations on Sets, and Complement of a Set.
NCERT Solutions Class 11 Maths Chapter 1 Sets are designed in a step-by-step format. It offers a deeper understanding of concepts to the students and helps them score high in competitive exams like JEE Main exams. If you want to explore the NCERT notes of Class 11 Maths with solved examples and important topics, explore Class 11 Maths NCERT Notes.
- Class 11 Chapter 1 Sets Exercise-wise NCERT Solutions
- Class 11 Chapter 1 Sets Exercise 1.1 Solutions
- Class 11 Chapter 1 Sets Exercise 1.2 Solutions
- Class 11 Chapter 1 Sets Exercise 1.3 Solutions
- Class 11 Chapter 1 Sets Exercise 1.4 Solutions
- Class 11 Chapter 1 Sets Exercise 1.5 Solutions
- Class 11 Chapter 1 Sets Exercise 1.6 Solutions
- Class 11 Chapter 1 Sets Miscellaneous Exercise NCERT Solutions
- Class 11 Chapter 1 Sets NCERT Solution PDF: Free PDF Download
- Important Formulas of Class 11 Maths Chapter 1 Sets
- Class 11 Chapter 1 Sets: Key Topics, Weightage and Important formulae
- Sets Chapter at a Glance – Class 11 Maths NCERT Solutions
- Class 11 Sets - FAQs
Class 11 Chapter 1 Sets Exercise-wise NCERT Solutions
Class 11 Sets chapter deals with many important topics, such as the definition and representation of Sets, and types of Sets; Finite, Infinite, Singleton, Universal, etc., Venn Diagrams, operations on sets. . Students will encounter problems related to different concepts and properties of Set Theory in these exercises. Candidates can check the exercise-wise Chapter 1 Class 11 math solutions below;
Class 11 Chapter 1 Sets Exercise 1.1 Solutions
Class 11 Chapter 1 Sets Exercise 1.1 focuses on building the basic conceptual understanding of Set, relation and function. Sets Exercise 1.1 deals with fundamental concepts such as the representation of sets (roster form and set-builder form), types of sets (finite, infinite, empty, equal, and equivalent sets), and Venn diagrams. the Class 11 Set Exercise 1.1 also focuses on operations on sets like union, intersection, and complement of sets. Exercise 1.1 Solutions includes a total of 6 Questions, all descriptive. Students can check the complete solution of Exercise 1.1 Below:
Class 11 Chapter 1 Set Exercise 1.1 NCERT SolutionsQ1. Which of the following are sets? Justify your answer. (i)The collection of all the months of a year beginning with the letter J. (ii)The collection of ten most talented writers of India. (iii)A team of eleven best-cricket batsmen of the world. (iv)The collection of all boys in your class. (v)The collection of all natural numbers less than 100. (vi)A collection of novels written by the writer Munshi Prem Chand. (vii)The collection of all even integers. (viii)The collection of questions in this Chapter. (ix)A collection of most dangerous animals of the world. |
| A.1. (i)The collection of all months of a year with J as initial are January, June and July. Hence, it is a well-defined and is therefore a set . (ii)The collection of ten most talented writers of India is not well-defined as it may vary from one person to another. Hence, it is not a set. (iii)The team of 11 best-cricket batsmen of the world is not well-defined as it may vary from one parson to another as they may vary from one person to another. Hence, it is not a set. (iv)The collection of all boys in your class is well-defined as your-class is fixed. Hence, it is a set. (v)The collection of all natural numbersless than 100 will be from 1 to 99. Hence, it is well-defined and is therefore a set. (vi)Novels written by writer Munshi Prem cham is a well-defined collection as he is no more so. Hence it is a set. (vii)The collection of all even integers is well-defined and hence is a set. (viii)The collection of questions in this chapter is well-defined and hence is a set. (ix)The collection of most dangerous animals of the world is not well-defined as it may vary from one person to another. |
| Q2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol or in the blank spaces: (i)5. . .A(ii)8 . . . A (iii)0. . .A (iv) 4. . . A (v) 2. . .A (vi) 10. . .A |
| A.2. (i)5 A(ii)8 A(iii)0 A (iv)4 A(v)2 A(vi)10 A |
| Q3. Write the following sets in roster form: (i)A = {x : x is an integer and –3< x < 7} (ii) B = {x : x is a natural number less than 6} (iii) C = {x : x is a two-digit natural number such that the sum of its digits is 8} (iv) D = {x : x is a prime number which is divisor of 60} (v) E = The set of all letters in the word TRIGONOMETRY (vi) F = The set of all letters in the word BETTER |
| A.3. (i)A = {– 3, –2, –1, 0, 1, 2, 3, 4, 5, 6} (ii)B = {1, 2, 3, 4, 5} (iii)C = {17, 26, 35, 44, 53, 62, 71, 80} (iv)x = Prime number which are divisor of 60 Factors of 60 are 1,2,3,4,5,6,10,12,15,20,30,60 Hence, x = 2, 3, 5 ⸫D = {2, 3, 5} (v) E = {T, R, I, G, O, N, M, E, Y} (vi) F = {B, E, T, R} |
| Q4. Write the following sets in the set-builder form: (i)(3, 6, 9, 12} (ii) {2,4,8,16,32} (iii) {5, 25, 125, 625} (iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100} |
| A.4. (i) {3,6,9,12}={3 × 1, 3 × 2, 3 × 3, 3 × 4} = {x : x = 3n, n is natural number and 1≤ n ≤ 4} (ii){2,4,8,16,32}={21, 22, 23, 24, 25} ={x : x = 2n, n is natural number and 1 ≤ n ≤ 5} (iii){5,25,125,625}={51, 52, 53, 54} ={x : x = 5n, n is natural number and 1 ≤ n ≤ 4} (iv){2,4,6,}={2 × 1, 2 × 2, 2 × 3, …} ={x : x = 2n, n is a natural number} (v){1,4,9, …, 100}={12, 22, 32, …, 102} = {x : x = n2, x is a natural number and 1 ≤ n ≤ 10} |
| Q5. List all the elements of the following sets : (i)A = {x : x is an odd natural number} (ii) B = {x : x is an integer, (iii) C = {x : x is an integer, } (iv)D = {x : x is a letter in the word “LOYAL”} (v) E = {x : x is a month of a year not having 31 days} (vi)F = {x : x is a consonant in the English alphabet which precedes k }. |
| A.5. (i)A = {1, 3, 5, 7, …} (ii)B ={0,1,2,3,4} (as =4.5 and = –0.5) (iii)x2 ≤ 4 x2 ≤ 22 x ≤ ± 2 So, C ={–2, –1,0,1,2} (vi)D = {L, O, Y, A} (v)E = {February, April, June, September, November} (vi)F = {b, c, d, f, g, h, j} |
| Q6. Match each of the set on the left in the roster form with the same set on the right described in set-builder form: (i){1, 2, 3, 6} (a) {x : x is a prime number and a divisor of 6} (ii) {2, 3} (b) {x : x is an odd natural number less than 10} (iii) {M,A,T,H,E,I,C,S} (c){x : x is natural number and divisor of 6} (iv) {1, 3, 5, 7, 9} (d){x : x is a letter of the word MATHEMATICS}. |
| A.6. (i)(i) (c) (ii) (a) (iii) (d) (iv) (b) |
Commonly asked questions
16. Write down all the subsets of the following sets
(i) {a}
(ii) {a, b}
(iii) {1, 2, 3}
(iv)
16 (i) Subset of {a} = {a}, .
(ii) Subset of {a, b} = ,{a},{b},{a, b}
(iii) Subset of {1,2,3} = ,{1},{2},{3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
(iv) Subset of = .
Class 11 Chapter 1 Set Ex 1.2 NCERT Solutions
7. Which of the following are examples of the null set
(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers
(iii) {x : x is a natural numbers, x < 5 and x > 7}
(iv) {y : y is a point common to any two parallel lines}
1. (i) There is no odd number that can be divided by 2.
?The given set is a null set.
(ii) An even prime number is 2. Hence, the set will have 2 as element.
? The given set is not a null set.
(iii) As there is no natural number which is both less than 5 and greater than 7.
? The given set is a null set.
(iv) Two parallel lines never meets and hence no common point.
? The given set is a null set.
3. Write the following sets in roster form:
(i) A = {x : x is an integer and –3< x < 7}
(ii) B = {x : x is a natural number less than 6}
(iii) C = {x : x is a two-digit natural number such that the sum of its digits is 8}
(iv) D = {x : x is a prime number which is divisor of 60}
(v) E = The set of all letters in the word TRIGONOMETRY
(vi) F = The set of all letters in the word BETTER
(i) A = {– 3, –2, –1, 0, 1, 2, 3, 4, 5, 6}
(ii) B = {1, 2, 3, 4, 5}
(iii) C = {17, 26, 35, 44, 53, 62, 71, 80}
(iv) x = Prime number which are divisor of 60
Factors of 60 are 1,2,3,4,5,6,10,12,15,20,30,60
Hence, x = 2, 3, 5
?D = {2, 3, 5}
(v) E = {T, R, I, G, O, N, M, E, Y}
(vi) F = {B, E, T, R}
40. Fill in the blanks to make each of the following a true statement :
(i) A A= . . .
(ii) A = . . .
(iii) A A= . . .
(iv)U A = . . .
40. (i) A A = U
(ii) ∩ A = U ∩ A = A.
(iii) A ∩ A = .
(iv) U ∩ A = ∩ A = .
19. Write the following intervals in set-builder form :
(i) (– 3, 0)
(ii) [6 , 12]
(iii) (6, 12]
(iv) [–23, 5)
19. (i) [–3, 0] = {x : x such that x R, –3 < x <0}
(ii) [6, 12] = {x : x R, 6 ≤ x ≤ 12}
(iii) (6, 12] = {x : x R, 6 < x ≤ 12}
(iv) [–23, 5) = {x : x R, –23 ≤ x < 5}
Sets Ex 1.4 Class 11 Math Solutions
Q22. Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x 6 }
B = {x : x is a natural number and 6 < x <10 }
(v) A = {1, 2, 3}, B =
22. (i) X∪ Y = {1,3,5}∪ {1,2,3} = {1,2,3,5}.
(ii) A ∪B = {a, e, i, o, u} ∪ {a, b, c} = {a, b, c, e, i, o, u}
(iii) A = {3, 6, 9, 12 …}
B = {1, 2, 3, 4, 5}
So, A∪ B = {3, 6, 9, 12, …}∪ {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5, 6, 9, 12 …}
(iv) A = {2, 3, 4, 5, 6}
B = {7, 8, 9}
So, A∪ B = {2, 3, 4, 5, 6}∪ {7, 8, 9} = {2, 3, 4, 5, 6, 7, 8, 9}
(v) A ∪B = {1, 2, 3} ∪ = {1, 2, 3}.
Class 11 Set Exercise 1.3 Solutions
13. Make correct statements by filling in the symbols or ? in the blank spaces :
(i) { 2, 3, 4 } . . . { 1, 2, 3, 4,5 }
(ii) { a, b, c } . . . { b, c, d }
(iii) {x : x is a student of Class XI of your school}. . .{x : x student of your school}
(iv) {x : x is a circle in the plane} . . .{x : x is a circle in the same plane with radius 1 unit}
(v) {x : x is a triangle in a plane} . . . {x : x is a rectangle in the plane}
(vi) {x : x is an equilateral triangle in a plane} . . . {x : x is a triangle in the same plane}
(vii) {x : x is an even natural number} . . . {x : x is an integer}
13. (i) {2,3,4} {1,2,3,4,5}
(ii) {a, b, c} ? {b, c, d}
(iii) {x : x is a student of class XI of yours school} {x : x is a student of your school}
(iv) As any circle in the plane can have radius more or less than 1 unit.
(x : x is a circle in the plane) ? {x : x is a circle in the same plane with radius 1 unit}
(v) As a triangle can never be a rectangle.
{x : x is a triangle in a plane} ? {x : x is a triangle in the same plane}
(vi) Any triangle in a plane can be scaler, isosceles, equilateral.
So. {x : x is a equilateral triangle in a plane} {x : x is a triangle in the same plane}
(vii) As all even natural number is also an integer.
{x : x is an even natural number} {x : x is an integer}.
18. Write the following as intervals:
(i) {x : x R, – 4 <x < 6}
(ii) {x : x R, – 12 < x < –10}
(iii) {x : x R, 0 x < 7}
(iv) {x : x R, 3 x 4}
18. (i) As x does not include –4 while 6 is included.
(–4, 6].
(ii) As x does not include both –12 and –10.
(–12, –10)
(iii) As x includes 0 but does not includes 7.
[0, 7)
(iv) As includes both 3 and 4
[3, 4]
43. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
43. Let H and E be set if people who speak Hindi and English respectively. there,
n (H) = 250, people speak Hindi n (E) = 200, people speak English
n (H E) = 400, people speaks either Hindi or English
So, n (H E) = n (H) + n (E) n (H E)
= 250 + 200 400
= 50
So, 50 people can speak both Hindi and English.
63. In a survey of 60 people, it was found that 25 people read newspaper H, 26 readnewspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T,8 read both T and I, 3 read all three newspapers. Find:
(i) The number of people who read at least one of the newspapers.
(ii) The number of people who read exactly one newspaper
63. Let H, T and I be of people who reads newspaper H, T and I respectively.
Then,
number of people who reads newspaper H, n (H) = 25.
number of people who T, n (T) = 26.
number of people who I, n (I) = 26
number of people who both H and T, n (HI) = 9
number of people who both H and T, n (H T) = 11
number of people who both T and I, n (TI) = 8
number of people who reads all newspaper, n (HTI) = 3.
Total no. of people surveyed = 60
The given sets can be represented by venn diagram

(i) The number of people who reads at least one of the newspaper.
in (H∪TI) = n (H) + n (T) + n (I) n (HT) n (HI) n (TI) + n (HTI)
= 25 + 26 + 26 11 9 8 + 3
= 80 28
= 52
(ii) From venn diagram,
a = number of people who reads newspapers H and T only.
b = number of people who reads newspapers H and I only.
c = number of people who reads newspapers T and I only.
d = number of people who reads all newspaper.
So, n (HT) = a + d.
n (HI) = b + d
n (TI) = c + d
So, a + d + c + d + b + d = n (HT) + n (HI) + n (TI)
a + d + c + b + 2d = 11 + 9 + 8
a + b + c +d = 28 - 2d
= 28 2 3 [d = n (HTI) = 3]
= 28 - 6
= 22
Number of people who reads exactly one newspaper
= Total no. of people - No. of people who reads more than one newspaper
= 52 - (a + b +c + d)
= 52 - 22
= 30
25. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find
(i) A B
(ii) A C
(iii) B C
(iv) B D
(v) A B C
(vi) A B D
(vii) B C D
25. (i) A B = {1, 2, 3, 4} {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
(ii) A C = {1, 2, 3, 4} {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B C = {3, 4, 5, 6} {5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
(iv) B D = {3, 4, 5, 6} {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}
(v) A B C = (A B) C = {1,2,3,4,5,6} {5,6,7,8}
= {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A B D = (A B) D = {1,2,3,4,5,6} {7,8,9,10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B C D = (B C) D = {3,4,5,6,7,8} {7,8,9,10}
= {3, 4, 5, 6, 7, 8, 9, 10}
48. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
48. Let A and B be set of people who speaks Frenchand Spanish respectively. Then,
n (A) = 50, people speak French
n (B) = 20, people speak Spanish.
n (A B) = 10, speaks both French& Spanish.
So, number of people who speaks at least one of these two languages
= n (A B)
= n (A) + n (B) n (A B)
= 50 + 20 10
= 60
62. In a group of students, 100 students know Hindi, 50 know English and 25 knowboth. Each of the students knows either Hindi or English. How many studentsare there in the group?
62. Let H and E be set of students who known Hindi and English respectively.
Then, number of students who know Hindi = n (H) = 100
Number of students who know English = n (E) = 50
Number of students who know both English & Hindi = 25 = n (HE)
As each of students knows either Hindi or English,
Total number of students in the group,
n (HE) = n (H) + n (E) - n (HE)
= 100 + 25
= 125,
Miscellaneous Exercise Chapter 1 Solutions
49. Decide, among the following sets, which sets are subsets of one and another:
A = { x: x R and x satisfy x2– 8x + 12 = 0 }, B = { 2, 4, 6 }, C = { 2, 4, 6, 8, . . . }, D = { 6 }.
49. A = {x: xR and x satisfy x2 - 8x + 12 = 0}
So, x2 - 8x + 12 = 0
x2 - 6x 2x + 12 = 0
x (x- 6) 2 (x -6) = 0
(x -6) (x- 2) = 0
x = 6, 2.
So, A = {2, 6) B = {2, 4, 6} C = {2, 4, 6, 8, ….}
D = {6}
D⊂ A ⊂B ⊂C
i e, D ⊂A, D⊂ B, D⊂ C, A⊂ B, A ⊂C and B⊂ C.
37. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that
(i) A B) = A ∩ B
(ii) A ∩ B) = A B
37. (i) L.H.S = (A B) = U – (A B)
= {1,2,3,4,5,6,7,8,9} – [ {2,4,6,8) {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2,3,4,5,6,7,8}
= {1,9}
R.H.S. = A ∩ B = [U – A] ∩ [U B]
= ∩
= {1,3,5,7,9} ∩ {1,4,6,8,9}
= {1,9}
? L.H.S. = R.H.S.
(A B) = A ∩ B.
(ii) L.H.S. = (A ∩ B) = U – (A ∩ B)
= {1,2,3,4,5,6,7,8,9} – [ {2,4,6,8} ∩ {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2}
= {1,3,4,5,6,7,8,9}
R.H.S. = A B
= [U – A] [U – B]
= [ {1,2,3,4,5,6,7,8,9} – {2,4,6,8}] [ {1,2,3,4,5,6,7,8,9} – {2,3,5,7}]
= {1,3,5,7,9} {1,4,6,8,9}
= {1,3,4,5,6,7,8,9}
? L.H.S. = R.H.S.
(A ∩ B) = A B.
45. If X and Y are two sets such that X has 40 elements, X Y has 60 elements and X Y has 10 elements, how many elements does Y have?
45. Given, n (X) = 40
n (Y Y) = 60.
n (X Y) = 10.
n (Y) =?
Using, n (X Y) = n (X) + n (Y) n (X Y)
60 = 40 + n (y) 10.
n (Y) = 60 - 40 + 10
n (Y) = 30.
44. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩T has 11 elements, how many elements does S T have?
44. Given, n (S) = 21
n (T) = 32
n (S T) = 11.
Using, n (S T) = n (S) + n (T) n (S T)
= 21 + 32 11
= 42.
2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol or in the blank spaces:
(i) 5. . .A
(ii) 8 . . . A
(iii) 0. . .A
(iv) 4. . . A
(v) 2. . .A
(vi) 10. . .A
2. (i) 5 A
(ii) 8 A
(iii) 0 A
(iv) 4 A
(v) 2 A
(vi) 10 A
50. In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x A and A B, then x B
(ii) If A B and B C, then A C
(iii) If A B and B C , then A C
(iv) If A B and B C, then A C
(v) If x A and A B , then x B
(vi) If A B and x B , then x A
50. (i) False Let A = {a}, a A then B = {a}, b} I e,
(ii) False. Let A. = {a}, if A B, B = {a, b} and B C I e, C = {a, b}, c} I e, A = {a}.
(iii) True. Let x
(iv) False. Let A = {a} and B = {b} then A
(v) False. Let A = {a} and B = {b} so, A
(vi) True. Let A
Then by above definition, A
15. Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
(i) {3, 4}
(ii) {3, 4}
(iii) {{3, 4}}
(iv) 1
(v) 1
(vi) {1, 2, 5}
(vii) {1, 2, 5}
(viii) {1, 2, 3}
(ix)
(x)
(xi) {
15. (i) False as 3
(ii) True as {3, 4}
(iii) True as {3, 4}
(iv) True as 1 is an element of A.
(v) False as 1 is not a set so it cannot be a subset of A.
(vi) True as 1
(vii) False as {1, 2, 5} is not an element of A.
(viii) False of 3
(ix) False as
(x) True,
(xi) False, as
4. Write the following sets in the set-builder form:
(i) (3, 6, 9, 12}
(ii) {2,4,8,16,32}
(iii) {5, 25, 125, 625}
(iv) {2, 4, 6, . . .}
(v) {1,4,9, . . .,100}
4. (i) {3,6,9,12}= {3 × 1, 3 × 2, 3 × 3, 3 × 4}
= {x : x = 3n, n is natural number and 1≤ n ≤ 4}
(ii) {2,4,8,16,32}= {21, 22, 23, 24, 25}
= {x : x = 2n, n is natural number and 1 ≤ n ≤ 5}
(iii) {5,25,125,625}= {51, 52, 53, 54}
= {x : x = 5n, n is natural number and 1 ≤ n ≤ 4}
(iv) {2,4,6, }= {2 × 1, 2 × 2, 2 × 3, …}
= {x : x = 2n, n is a natural number}
(v) {1,4,9, …, 100}= {12, 22, 32, …, 102}
= {x : x = n2, x is a natural number and 1 ≤ n ≤ 10}
39. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A
39. A
= Set of all triangle in a plane - Set of all triangle with at least the angle different from 60°.
= Set of all triangle with each angle 60°.
A? = set of all equilateral triangle.
64. In a survey it was found that 21 people liked product A, 26 liked product B and29 liked product C. If 14 people liked products A and B, 12 people liked productsC and A, 14 people liked products B and C and 8 liked all the three products.Find how many liked product C only.
64. Let A, B and C be the set of people who like product A, B and C respectively.
Then,
Number of people who like product A, n (A) = 21
Number of people who like product B, n (B) = 26
Number of people who like product C, n (C) = 29.
Number of people likes both product A and B, n (A
Number of people likes both product A and C, n (A
Number of people likes both product B and C, n (B
No. of people who likes all product, n (A
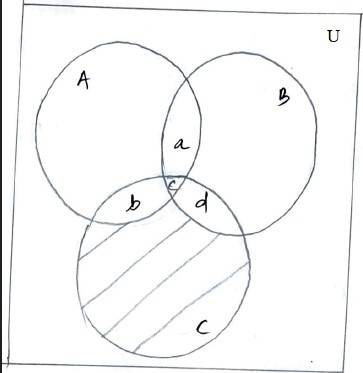
a→n (A
b→n (A
d→n (B
c→n (A
From the above venn diagram we can see that,
Number of people who likes product C only
= n (C) - b - d + c
= n (C) - n (A
= 29 - 12 - 14 + 8
= 11
57. Using properties of sets, show that
(i) A
(ii) A
57. (i) We know that,
A
(A
[A
[A
and also
A
So, A
(ii) A
= A
= A as (A
8. Which of the following sets are finite or infinite
(i) The set of months of a year
(ii) {1, 2, 3, . . .}
(iii) {1, 2, 3, . . ., 99, 100}
(iv) The set of positive integers greater than 100
(v) The set of prime numbers less than 99
8. (i) The set of months of a year has 12 elements. Here, the set is finite.
(ii) The given set has the natural number as its elements. Hence, the set is infinite.
(iii) The given set has 100 elements i.e., from 1 to 100. Hence, the set is finite.
(iv) There are infinite numbers of positive integers greater than 100. Hence the set is infinite.
(v) The numbers of prime number less than 99 is finite. Hence, the set is finite.
61. In a survey of 600 students in a school, 150 students were found to be taking teaand 225 taking coffee, 100 were taking both tea and coffee. Find how manystudents were taking neither tea nor coffee?
61. Let T and C be sets of students taking tea and coffee.
Then, n (T) = 150, number of students taking tea
n (C) = 225, number of students taking coffee
n (T
So, Number of students taking either tea or coffee is.
n (T
= 150 + 225 100
= 275
Number of students taking neither tea coffee
= Total number of students No of students taking either tea or coffee
= 600 275
= 325.
55. Is it true that for any sets A and B, P (A)
55. Let A = {a}, B = {b}.
So, P (A) =
So, P (A)
Now, A
P (A
So. From (1) and (2) we see that,
P (A)
27. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find
(i) A
(ii) B
(iii) A
(iv) A
(v) B
(vi) A
(vii) A
(viii) A
(ix) (A
(x) (A
27. (i) A ∩ B = {3,5,7,9,11} ∩ {7,9,11,13}
= {7, 9, 11}
(ii) B ∩ C = {7,9,11,13} ∩ {11,13,15}
= {11,13}
(iii) A ∩ C ∩ D = (A ∩ C) ∩ D
= [ {3,5,7,9,11} ∩ {11,13,15}] ∩ {15,17}.
= {11} ∩ {15,17} =
(iv) A ∩ C = {3,5,7,9,11} ∩ {11,13,15}.
= {11}
(v) B ∩ D = {7,9,11,13} ∩ {15,17}=
(vi) A ∩ (B∪ C) = {3,5,7,9,11} ∩ [ {7,9,11,13}∪ {11,13,15}]
= {3,5,7,9,11} ∩ {7,9,11,13,15}.
= {7,9,11}
(vii) A ∩ D = {3,5,7,9,11} ∩ {15,17} =
(viii) A ∩ (B ∪ D) = {3,5,7,9,11} ∩ [ {7,9,11,13} ∪ {15,17}]
= {3,5,7,9,11} ∩ {7,9,11,13,15,17}
= {7,9,11}
(ix) (A ∩ B) ∩ (B ∪ C) = [ {3,5,7,9,11} ∩ {7,9,11,13}] ∩ [ {7,9,11, 13} ∪ {11,13, 15}]
= {7,9,11} ∩ {7,9,11,13,15}
= {7,9,11}.
(x) (A ∪ D) ∩ (B ∪ C) = [ {3,5,7,9,11} ∪ {15,17}] ∩ [ {7, 9, 11, 13} ∪ {11, 13, 15}
= {3,5,7,9,11,15,17} ∩ {7,9,11,13,15}
= {7,9,11,15}.
28. If A = {x : x is a natural number }, B = {x : x is an even natural number}
C = {x : x is an odd natural number} and D = {x : x is a prime number }, find
(i)A
(ii) A
(iii) A
(iv) B
(v) B
(vi) C
28. A = {1,2,3,4,5, 6, …}
B = {2,4,6, …}
C = {1,3,5, …}
D = {2,3,5, …, }
(i) A ∩ B = {1,2,3,4 …} ∩ {2,4,6, …} = {2,4,6 …} = B.
(ii) A ∩ C = {1,2,3,4, …} ∩ {1,3,5 …} = {1,3,5, …} = C.
(iii) B ∩ C = {2,4,6, …} ∩ {1,3,5, …} =
(iv) B ∩ D = {2,4,6 …} ∩ {2,3,5 …} = {2}
(v) C ∩ D = {1,3,5, …} ∩ {2,3,5 …} = {3,5,7 …} = {x : x is odd prime number}
42. If X and Y are two sets such that X
42. Given, n (X
n (X) = 8.n (Y) = 15.n (X
Using n (X
= 8 + 15 18.
= 5.
60. Find sets A, B and C such that A
60. Let A = {x, y}
B = {y, z}
C = {x, z}
So, A
B
A
But A
= {y}
=
51. Let A, B, and C be the sets such that A
51. Let x
As B
Let x
as A
x
i.e., x
when x
x
But A
So, x
i.e., x
x
when, x
as x
So, B
Similarly, C
So, B = C
6. Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
(i) {1, 2, 3, 6} (a) {x : x is a prime number and a divisor of 6}
(ii) {2, 3} (b) {x : x is an odd natural number less than 10}
(iii) {M,A,T,H,E,I,C,S} (c) {x : x is natural number and divisor of 6}
(iv) {1, 3, 5, 7, 9} (d) {x : x is a letter of the word MATHEMATICS}.
6. (i) (c)
(ii) (a)
(iii) (d)
(iv) (b)
Class 11 Sets Exercise 1.6 Solutions
41. If X and Y are two sets such that n( X ) = 17, n ( Y ) = 23 and n(X
41. Given, n (X)= 17
n (Y) = 23
n (X
So, n (X
n (X
= 17 + 23 38.
= 2
21. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C
(i) {0, 1, 2, 3, 4, 5, 6}
(ii)
(iii) {0,1,2,3,4,5,6,7,8,9,10}
(iv) {1,2,3,4,5,6,7,8}
21. Universal set of A, B and C must includes all elements of A, B and C, i.e. 0,1,2,3,4,5,6,8.
So, the universal set of A, B and C is (iii) {0,1,2,3,4,5,6,7,8,9,10}.
Exercise 1.5 Class 11 Maths Solutions
34. Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } andC = { 3, 4, 5, 6 }. Find
(i) A
(ii) B
(iii) (A
(iv) (A
(v) (A
(vi) (B – C)
34. (i) A
= {5,6,7,8,9}
(ii) B
= {1,3,5,7,9}.
(iii) (A
= {5,6,7,8,9} ∩ [U – C] [? (i)]
= {5,6,7,8,9} ∩ [ {1,2,3,4,5,6,1,8,9} – {3,4,5,6}]
= {5,6,7,8,9} ∩ {1,2,7,8,9}
= {7,8,9}
(iv) A
= {5,6,7,8,9} ∩ {1,3,5,7,9} [? (i) and (ii)]
= {5,7,9}.
(v) (A
= {1,2,3,4} = A
(A
(vi) (B – C)
= {1,2,3,4,5,6,7,8,9} – {2,8}
= {1,3,4, 5, 6,7,9}.
52. Show that the following four conditions are equivalent :
(i) A
52. (i) Let A- B≠
i.e., x
But as A B, the above condition of assumption is wrong if A
(ii) Let x
As A - B =
if A - B =
(iii) We know that,
B
Let x
As A
If x
So, (A
(iv) We know that,
(A
Let x
So, x
i.e., A
So, A = (A
Hence, A
A - B =
A
A
i.e., the 4 conditions are equivalent.
Class 11 Chapter 1 Set Exercise 1.1 NCERT Solutions
1. Which of the following are sets? Justify your answer.
(i) The collection of all the months of a year beginning with the letter J.
(ii) The collection of ten most talented writers of India.
(iii) A team of eleven best-cricket batsmen of the world.
(iv) The collection of all boys in your class.
(v) The collection of all natural numbers less than 100.
(vi) A collection of novels written by the writer Munshi Prem Chand.
(vii) The collection of all even integers.
(viii) The collection of questions in this Chapter.
(ix) A collection of most dangerous animals of the world.
1. (i) The collection of all months of a year with J as initial are January, June and July. Hence, it is a well-defined and is therefore a set
(ii) The collection of ten most talented writers of India is not well-defined as it may vary from one person to another. Hence, it is not a set.
(iii) The team of 11 best-cricket batsmen of the world is not well-defined as it may vary from one parson to another as they may vary from one person to another. Hence, it is not a set.
(iv) The collection of all boys in your class is well-defined as your-class is fixed. Hence, it is a set.
(v) The collection of all natural numbersless than 100 will be from 1 to 99. Hence, it is well-defined and is therefore a set.
(vi) Novels written by writer Munshi Prem cham is a well-defined collection as he is no more so. Hence it is a set.
(vii) The collection of all even integers is well-defined and hence is a set.
(viii) The collection of questions in this chapter is well-defined and hence is a set.
(ix) The collection of most dangerous animals of the world is not well-defined as it may vary from one person to another.
11. Are the following pair of sets equal? Give reasons.
(i) A = {2, 3}, B = {x : x is solution of x2+ 5x + 6 = 0}
(ii) A = { x : x is a letter in the word FOLLOW}
(iii) B = { y : y is a letter in the word WOLF}
11. (i) A = {2, 3)
B = {x : x is solution of x2 + 5x + 6 = 0}
So, x2 + 5x + 6 = 0
x2 + 2x + 3x + 6 = 0
x (x+2) + 3 (x+2) = 0
(x+2) (x+3) = 0
x = –2, –3
So, B = {–2, –3}
So, A ≠ B.
(ii) A = {x : x is a letter in word FOLLOW}
A = {F, O, L, W}
(iii) B = {x : x is a letter in word WOLF}
B = {W, O, L, F}
So, A = B as the elements are all same.
9. State whether each of the following set is finite or infinite:
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0,0)
9. (i) We can draw infinite number of lines parallel to x-axis.
∴ The set is infinite.
(ii) There are 26 letters in the English alphabet.
∴ The set is finite.
(iii) There are infinite number which are a multiple of 5.
∴ The set is infinite
(iv) The numbers of animals living on earth are finite.
∴ The set is finite.
(v) There can be infinite number of circular passing through origin (0,0).
∴ The set is infinite.
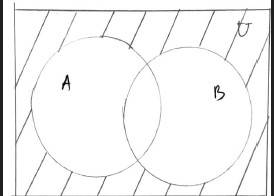
38. Draw appropriate Venn diagram for each of the following :
(i) (A
38. (i) (A
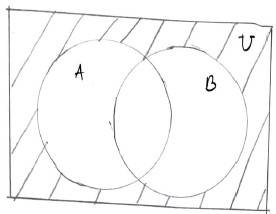
(ii) A
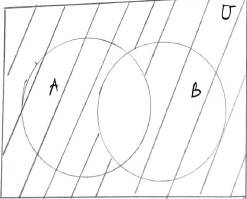
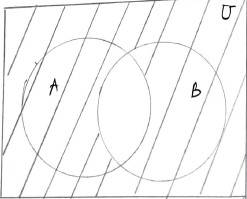
29. Which of the following pairs of sets are disjoint
(i) {1, 2, 3, 4} and {x : x is a natural number and
(ii) {a, e, i, o, u } and { c, d, e, f }
(iii) {x : x is an even integer} and {x : x is an odd integer}
29. (i) {1,2,3,4} ∩ {x : x is a natural number and 4 ≤ x ≤ 6}
{1, 2, 3, 4} ∩ {4, 5, 6}
{4} ≠∅
Hence, the given pair of set is not disjoint.
(ii) {a, e, i, o, u} ∩ {c, d, e, f}
{e} ≠∅
Hence, the given pair of set is not disjoint.
(iii) {x: x is an even integer} ∩ {x: x is are odd integer}.
=∅
As there is no integer which is both even and odd at the same time.
? Given pair of set are disjoint.
5. List all the elements of the following sets :
(i) A = {x : x is an odd natural number}
(ii) B = {x : x is an integer,
(iii) C = {x : x is an integer,
(iv) D = {x : x is a letter in the word “LOYAL”}
(v) E = {x : x is a month of a year not having 31 days}
(vi) F = {x : x is a consonant in the English alphabet which precedes k }.
5. (i) A = {1, 3, 5, 7, …}
(ii) B = {0,1,2,3,4} (as
(iii) x2 ≤ 4
x2 ≤ 22
x ≤ ± 2
So, C = {–2, –1,0,1,2}
(iv) D = {L, O, Y, A}
(v) E = {February, April, June, September, November}
(vi) F = {b, c, d, f, g, h, j}
46. In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
46. Let A and B but the set of people who likes coffee and tea.
Then, n (A) = 37. no. of people who like coffee
n (B) = 52, no. of people who like tea.
As each person likes at least one of the two drink,
n (A
So using, n (A
n (A
= 37 + 52 70
= 89 70
= 19
So, 19 people likes both coffee and tea.
10. In the following, state whether A = B or not:
(i) A = { a, b, c, d } B = { d, c, b, a }
(ii) A = { 4, 8, 12, 16 } B = { 8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10} B = { x : x is positive even integer and x < 10}
(iv) A = { x : x is a multiple of 10}, B = { 10, 15, 20, 25, 30, . . . }
10. (i) As A and B has a, b, c and d as elements and are exactly the same, Hence, A = B.
(ii) Hence, 12
Similarly 18
So, A ≠ B.
(iii) A = {2,4,6,8,10} and B = {2,4,6,8,10}
So, A=B.
(iv) A= {10,20,30,40, …} and B= {10,15,20,25,30, …}
So, A ≠ B.
53. Show that if A
53. Given, A
Let x
However, A
i.e., X
So, x
C - B
12. From the sets given below, select equal sets :
A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2}
E = {–1, 1}, F = { 0, a}, G = {1, –1}, H = { 0, 1}
12. B = D = {1, 2, 3, 4} = {3, 1, 4, 2}
E = G = {–1, 1} = {1, –1}.
14. Examine whether the following statements are true or false:
(i) { a, b } ? { b, c, a }
(ii) { a, e }
(iii) { 1, 2, 3 }
(iv) { a }
(v) { a }
(vi) { x : x is an even natural number less than 6}
14. (i) False as every element of set {a, b} is also an element of {b, c, a} hence {a, b }
(ii) True as every element in {a, e} is also a vowel in English alphabet.
(iii) False as 2
(iv) True as a
(v) False as a
(vi) {x : x is an even natural number less than 6} = {2, 4}
{x : x is a natural number which divides 36} = {1, 2, 3, 4, 6, 9, 12, 18, 36}
As {2, 4}
It is true.
30. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find
(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
(xi) C – D
(xii) D – C
30. (i) A – B = {3,6,9,12,15,18,21} – {4,8,12,16,20}
= {3,6,9,15,18,21}
(ii) A – C = {3,6,9,12,15,18,21} – {2,4,6,8,10,12,14,16}
= {3,9,15,18,21}
(iii) A – D = {3,6,9,12,15,18,21} – {5,10,15,20}
= {3,6,9,12,18,21}
(iv) B – A = {4,8,12,16,20} – {3,6,9,12,15,18,21}
= {4,8,16,20}
(v) C – A = {2,4,6,8,10,12,14,16} – {3,6,9,12,15,18,21}
= {2,4,8,10,14,16}
(vi) D – A = {5,10,15,20} – {3,6,9,12,15,18,21}
= {5,10,20}
(vii) B – C= {4,8,12,16,20} – {2,4,6,8,10,12,14,16}
= {20}
(viii) B – D = {4,8,12,16,20} – {5,10,15,20}
= {4,8,12,16}
(ix) C – B = {2,4,6,8,10,12,14,16} – {4,8,12,16,20}
= {2,6,10,14}
(x) D – B = {5,10,15,20} – {4,8,12,16,20}
= {5,10,15}
(xi) C – D = {2,4,6,8,10,12,14,16} – {5,10,15,20}
= {2,4,6,8,12,14,16}
(xii) D – C = {5,10,15,20} – {2,4,6,8,10,12,14,16}
= {5,15,20}
59. Let A and B be sets. If A
59. Let A, B and x be sets such that,
A
We know that,
A = A
= A
= (A
= (A
=> A = A∩ B [? A ∪? = A]
And B =
= B
= (B
= (B
B = B
So, A = B = A
47. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
47. Let C and T be the set of people who likes cricket and tennis respectively. Then,
n (C) = 40, people who likes cricket
n (C
and n (C
So, n (C
65 = 40 + n (T) 10
n (T) = 35
So, 35 people likes tennis
And number of people who likes tennis only and not cricket
(TC) = n (T) n (C
20. What universal set(s) would you propose for each of the following:
(i) The set of right triangles.
(ii) The set of isosceles triangles.
20. (i) The set of all triangles. U= {x : x is a triangle in a plane}
(ii) The set of all triangles. U= {x : x is a triangle in a plane}
58. Show that A
58. Let A = {a}, B = {a, b}, C = {a, c}
So, A
A
i.e., A
But B ≠C. as b
36. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x : x is an even natural number}
(ii) { x : x is an odd natural number }
(iii) {x : x is a positive multiple of 3}
(iv) { x : x is a prime number }
(v) {x : x is a natural number divisible by 3 and 5}
(vi) {x : x is a perfect square }
(vii) { x : x is a perfect cube}
(viii) {x : x + 5 = 8 }
(ix) { x : 2x + 5 = 9}
(x) {x : x
3. (i) {x : x is an odd natural number}
(ii) {x : x is an even natural number}
(iii) {x : x is not a multiple of 3}
(iv) {x : x is a positive composite number and x = 1}
(v) {x : x is a natural number not divisible by 3 and 5}.
(vi) {x : x is not a perfect square}
(vii) {x : x is not a perfect cube}
(viii) We have, x + 5 = 8.
x = 8 – 5 = 3
x = 3
? {x : x ≠ 3, x? N}
(ix )We have,
2x + 5 = 9
2x = 9 – 5
2x = 4
x = 2
? {x : x? N and x ≠ 2}
(x) {x : x < 7} = {1,2,3,4,5,6}
(xi) We have,
2x + 1 >10
2x >10 – 1
x >
?
35. If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets :
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g} (iv) D = { f, g, h, a}
35. (i) A
= {d, e, f, g, h}
(ii) B
= {a, b, c, h}.
(iii) C
= {b, d, f, h}
(iv) D
= {b, c, d, e}
17. How many elements has P(A), if A =
17. As A=
n(A) = 0 = m
So, n[P(A)] = 2m = 20 = 1.
33. State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u} and {a, b, c, d}are disjoint sets.
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
33. (i) False, as {2,3,4,5} ∩ {3,6} = {3} ≠
(ii) False as {a, e, i, o, u} ∩ {a, b, c, d} = {a} ≠
(iii) True as {2,6,10,14} ∩ {3,7,11,15} =
(iv) True as {2,6,10} ∩ {3,7,11}=
56. Show that for any sets A and B, A = ( A
56. Here,
(A
= A
= A
= A
And (A
= (A
= (A
= A
23. Let A = { a, b }, B = { a, b, c}. Is A
23. Given, A = {a, b}
B = {a, b, c}
Yes A
And A
31. If X= { a, b, c, d } and Y = { f, b, d, g}, find
(i) X – Y
(ii) Y – X
(iii) X ∩ Y
31. (i) X – Y = {a, b, c, d} – (f, b, d, g}
= {a, c}
(ii) Y – X = {f, b, d, g} – {a, b, c, d}
= {f, g}
(iii) X ∩ Y = {a, b, c, d} ∩ {f, b, d, g}
= {b, d}.
54. Assume that P (A) = P (B). Show that A = B.
54. Given, P (A) = P (B) where P is power set
Let x
Then, {x}
i.e., x
A
Similarly, B
A = B
24. If A and B are two sets such that A
24.If A? B then let a
but b
So, A
= {a, b}
= B
26. Find the intersection of each pair of sets of question 1 above.
26. (i) X ∩ Y = {1,3,5} ∩ {1,2,3} = {1,3}
(ii) A = {a, e, i, o, u} ∩ {a, b, c} = {a}
(iii) A ∩ B = {3,6,9,12 …} ∩ {1,2,3,4,5}
= {3}
(iv) A ∩ B = {2,3,4,5,6} ∩ {7,8,9} =
(v) A ∩ B = {1,2,3} ∩
32. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
32. R – Q = {x: x is a real number but not rational number}
= {x: x is an irrational number}
Since real number = rational number + irrational number
Class 11 Chapter 1 Sets Exercise 1.2 Solutions
Class 11 Chapter 1 Sets Exercise 1.2 introduces important operations and properties of Set Theory. This Exercise 1.2 focuses on subsets, power sets, universal sets, and Venn diagrams, which are key to understanding Set Theory. Exercise 1.2 of class 11 Sets also explores operations on sets, including union, intersection, difference, and complement of set. Class 11 Set Exercise 1.2 Solutions consists of answers to 6 Questions. Students can check the complete solution of Exercise 1.2 Below;
Class 11 Chapter 1 Set Ex 1.2 NCERT SolutionsQ1. Which of the following are examples of the null set (i) Set of odd natural numbers divisible by 2 (ii) Set of even prime numbers (iii) {x : x is a natural numbers, x < 5 and x > 7} (iv) {y : y is a point common to any two parallel lines} |
| A.l. (i)There is no odd number that can be divided by 2. ⸫The given set is a null set. (ii)An even prime number is 2. Hence, the set will have 2 as element. ⸫ The given set is not a null set. (iii)As there is no natural number which is both less than 5 and greater than 7. ⸫ The given set is a null set. (iv)Two parallel lines never meets and hence no common point. ⸫ The given set is a null set. |
| Q2. Which of the following sets are finite or infinite (i) The set of months of a year (ii) {1, 2, 3, . . .} (iii) {1, 2, 3, . . ., 99, 100} (iv) The set of positive integers greater than 100 (v) The set of prime numbers less than 99 |
| A.2. (i)The set of months of a year has 12 elements. Here, the set is finite. (ii)The given set has the natural number as its elements. Hence, the set is infinite. (iii)The given set has 100 elements i.e., from 1 to 100. Hence, the set is finite. (iv)There are infinite numbers of positive integers greater than 100. Hence the set is infinite. (v)The numbers of prime number less than 99 is finite. Hence, the set is finite. |
| Q3. State whether each of the following set is finite or infinite: (i) The set of lines which are parallel to the x-axis (ii) The set of letters in the English alphabet (iii) The set of numbers which are multiple of 5 (iv) The set of animals living on the earth (v) The set of circles passing through the origin (0,0) |
| A.3. (i)We can draw infinite number of lines parallel to x-axis. ⸫The set is infinite. (ii)There are 26 letters in the English alphabet. ⸫The set is finite. (iii)There are infinite number which are a multiple of 5. ⸫The set is infinite (iv)The numbers of animals living on earth are finite. ⸫The set is finite. (v)There can be infinite number of circular passing through origin (0,0). ⸫The set is infinite. |
| Q4. In the following, state whether A = B or not: (i) A = { a, b, c, d } B = { d, c, b, a } (ii) A = { 4, 8, 12, 16 } B = { 8, 4, 16, 18} (iii) A = {2, 4, 6, 8, 10} B = { x : x is positive even integer and x < 10} (iv) A = { x : x is a multiple of 10}, B = { 10, 15, 20, 25, 30, . . . } |
| A.4. (i)As A and B has a, b, c and d as elements and are exactly the same, Hence, A = B. (ii)Hence, 12
Similarly 18
So, A ≠ B. (iii)A = {2,4,6,8,10} and B = {2,4,6,8,10} So, A=B. (v)A={10,20,30,40, …} and B={10,15,20,25,30, …} So, A ≠ B. |
| Q5. Are the following pair of sets equal? Give reasons. (i) A = {2, 3}, B = {x : x is solution of x2+ 5x + 6 = 0} (ii) A = { x : x is a letter in the word FOLLOW} B = { y : y is a letter in the word WOLF} |
| A.5. (i)A = {2, 3) B = {x : x is solution of x2 + 5x + 6 = 0} So, x2 + 5x + 6 = 0 x2 + 2x + 3x + 6 = 0 x(x+2) + 3(x+2) = 0 (x+2)(x+3) = 0 x = –2, –3 So, B = {–2, –3} So, A ≠ B. (ii)A = {x : x is a letter in word FOLLOW} A = {F, O, L, W} B = {x : x is a letter in word WOLF} B = {W, O, L, F} So, A = B as the elements are all same. |
| Q6.From the sets given below, select equal sets : A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2} E = {–1, 1}, F = { 0, a}, G = {1, –1}, H = { 0, 1} |
| A.6. B = D = {1, 2, 3, 4} = {3, 1, 4, 2} E = G = {–1, 1} = {1, –1}. |
Class 11 Chapter 1 Sets Exercise 1.3 Solutions
Class 11 Math Chapter 1 Sets Exercise 1.3 focuses on the algebra of sets, introducing important properties and identities that govern set operations. This section explores laws of union and intersection, such as commutative, associative, and distributive laws, which help simplify complex set expressions. Additionally, it covers De Morgan’s Laws, which provide a systematic way to find the complement of set operations. Exercise 1.3 Solutions consists of 9 Questions, all descriptive. Students can check the complete solution of Exercise 1.3 Below
Class 11 Set Exercise 1.3 SolutionsQ1. Make correct statements by filling in the symbols
(i) { 2, 3, 4 } . . . { 1, 2, 3, 4,5 } (ii) { a, b, c } . . . { b, c, d } (iii) {x : x is a student of Class XI of your school}. . .{x : x student of your school} (iv) {x : x is a circle in the plane} . . .{x : x is a circle in the same plane with radius 1 unit} (v) {x : x is a triangle in a plane} . . . {x : x is a rectangle in the plane} (vi) {x : x is an equilateral triangle in a plane} . . . {x : x is a triangle in the same plane} (vii) {x : x is an even natural number} . . . {x : x is an integer} |
| A.1. (i){2,3,4}
(ii){a, b, c} ₡ {b, c, d} (iii){x : x is a student of class XI of yours school}
(iv)As any circle in the plane can have radius more or less than 1 unit. (x : x is a circle in the plane) ₡ {x : x is a circle in the same plane with radius 1 unit} (v)As a triangle can never be a rectangle. {x : x is a triangle in a plane} ₡ {x : x is a triangle in the same plane} (vi)Any triangle in a plane can be scaler, isosceles, equilateral. So. {x : x is a equilateral triangle in a plane}
(vii)As all even natural number is also an integer. {x : x is an even natural number}
|
| Q2. Examine whether the following statements are true or false: (i) { a, b } ₡ { b, c, a } (ii) { a, e }
(iii) { 1, 2, 3 }
(iv) { a }
(v) { a }
(vi) { x : x is an even natural number less than 6}
|
| A.2. (i)False as every element of set {a, b} is also an element of {b, c, a} hence {a, b }
(ii)True as every element in {a, e} is also a vowel in English alphabet. (iii)False as 2
(iv)True as a
(v)False as a
(vi){x : x is an even natural number less than 6} = {2, 4} {x : x is a natural number which divides 36} = {1, 2, 3, 4, 6, 9, 12, 18, 36} As {2, 4}
It is true. |
| Q.3. Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why? (i) {3, 4}
(iv) 1
(vii) {1, 2, 5}
(x)
|
| A.3. (i)False as 3
(ii)True as {3, 4}
(iii)True as {3, 4}
(iv)True as 1 is an element of A. (v)False as 1 is not a set so it cannot be a subset of A. (vi)True as 1
(vii)False as {1, 2, 5} is not an element of A. (viii)False of 3
(ix)False as
(x)True,
(xi)False, as
|
| Q4. Write down all the subsets of the following sets (i) {a}(ii) {a, b}(iii) {1, 2, 3} (iv)
|
| A.4. (i)Subset of {a} = {a},
(ii)Subset of {a, b} =
(iii)Subset of {1,2,3} =
(iv)Subset of
|
| Q5. How many elements has P(A), if A =
|
| A.5. As A=
n(A) = 0 = m So, n[P(A)] = 2m = 20 = 1. |
| Q6. Write the following as intervals: (i) {x : x
(iii) {x : x
|
| A.6. (i)As x does not include –4 while 6 is included. (–4, 6]. (ii)As x does not include both –12 and –10. (–12, –10) (iii)As x includes 0 but does not includes 7. [0, 7) (iv)As includes both 3 and 4 [3, 4] |
| Q7. Write the following intervals in set-builder form : (i) (– 3, 0) (ii) [6 , 12] (iii) (6, 12] (iv) [–23, 5) |
| A.7. (i)[–3, 0] = {x : x such that x
(ii)[6, 12] = {x : x
(iii)(6, 12] = {x : x
(iv)[–23, 5) = {x : x
|
| Q8. What universal set(s) would you propose for each of the following: (i)The set of right triangles. (ii) The set of isosceles triangles. |
| A.8. (i)The set of all triangles. U= {x : x is a triangle in a plane} (ii) The set of all triangles. U= {x : x is a triangle in a plane} |
| Q9. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C (i) {0, 1, 2, 3, 4, 5, 6} (ii)
(iii) {0,1,2,3,4,5,6,7,8,9,10} (iv) {1,2,3,4,5,6,7,8} |
| A.9. Universal set of A, B and C must includes all elements of A, B and C, i.e. 0,1,2,3,4,5,6,8. So, the universal set of A, B and C is (iii) {0,1,2,3,4,5,6,7,8,9,10}. |
Class 11 Chapter 1 Sets Exercise 1.4 Solutions
Class 11 Chapter 1 Sets Exercise 1.4 focuses on the practical applications of set theory, particularly in solving problems using the principle of inclusion and exclusion. Class 11 Math Exercise 1.4 is very important to understand counting elements in unions and intersections of multiple sets efficiently. Many important concepts such as finite and infinite sets, cardinality of sets, and methods to determine the number of elements in given set operations are discussed in Exercise 1.4 of Class 11 Sets. Class 11 Sets Exercise 1.4 consists of 12 questions (11 descriptive and 1 true and false). Students can check solutions to all 12 questions in Exercise 1.4 Below.
Sets Ex 1.4 Class 11 Math SolutionsQ1. Find the union of each of the following pairs of sets: (i) X = {1, 3, 5} Y = {1, 2, 3} (ii) A = [ a, e, i, o, u} B = {a, b, c} (iii) A = {x : x is a natural number and multiple of 3} B = {x : x is a natural number less than 6} (iv) A = {x : x is a natural number and 1 < x
B = {x : x is a natural number and 6 < x <10 } (v) A = {1, 2, 3}, B =
|
| A.1. (i)X∪ Y = {1,3,5}∪ {1,2,3} = {1,2,3,5}. (ii)A ∪B = {a, e, i, o, u} ∪{a, b, c} = {a, b, c, e, i, o, u} (iii)A = {3, 6, 9, 12 …} B = {1, 2, 3, 4, 5} So, A∪ B = {3, 6, 9, 12, …}∪ {1, 2, 3, 4, 5} = {1, 2, 3, 4, 5, 6, 9, 12 …} (iv)A = {2, 3, 4, 5, 6} B = {7, 8, 9} So, A∪ B = {2, 3, 4, 5, 6}∪ {7, 8, 9} = {2, 3, 4, 5, 6, 7, 8, 9} (v)A ∪B = {1, 2, 3} ∪
|
| Q2. Let A = { a, b }, B = { a, b, c}. Is A
|
| A.2. Given,A = {a, b} B = {a, b, c} Yes A
And A
|
| Q3.If A and B are two sets such that A
|
| A.3.If A ⸦ B then let a
but b
So, A
= {a, b} = B |
| Q4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find (i) A
(v) A
|
| A.4. (i)A
= {1, 2, 3, 4, 5, 6} (ii)A
= {1, 2, 3, 4, 5, 6, 7, 8} (iii)B
= {3, 4, 5, 6, 7, 8} (iv)B
= {3, 4, 5, 6, 7, 8, 9, 10} (v)A
= {1, 2, 3, 4, 5, 6, 7, 8} (vi)A
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (vii)B
= {3, 4, 5, 6, 7, 8, 9, 10} |
| Q5. Find the intersection of each pair of sets of question 1 above. |
| A.5. (i)X ∩ Y = {1,3,5} ∩ {1,2,3} = {1,3} (ii)A = {a, e, i, o, u} ∩ {a, b, c} = {a} (iii)A ∩ B = {3,6,9,12 …} ∩ {1,2,3,4,5} = {3} (iv)A ∩ B = {2,3,4,5,6} ∩ {7,8,9} =
(v)A ∩ B = {1,2,3} ∩
|
| Q6. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find (i) A
(iv) A
(vii) A
(x) (A
|
| A.6. (i)A ∩ B = {3,5,7,9,11} ∩ {7,9,11,13} = {7, 9, 11} (ii)B ∩ C = {7,9,11,13} ∩ {11,13,15} = {11,13} (iii)A ∩ C ∩ D = (A ∩ C) ∩ D = [{3,5,7,9,11} ∩ {11,13,15}] ∩ {15,17}. = {11} ∩ {15,17} =
(iv)A ∩ C = {3,5,7,9,11} ∩ {11,13,15}. = {11} (v)B ∩ D = {7,9,11,13} ∩ {15,17}=
(vi)A ∩ (B∪ C) = {3,5,7,9,11} ∩ [{7,9,11,13}∪ {11,13,15}] = {3,5,7,9,11} ∩ {7,9,11,13,15}. = {7,9,11} (vii)A ∩ D = {3,5,7,9,11} ∩ {15,17} =
(viii)A ∩ (B ∪ D) = {3,5,7,9,11} ∩ [{7,9,11,13} ∪ {15,17}] = {3,5,7,9,11} ∩ {7,9,11,13,15,17} = {7,9,11} (ix)(A ∩ B) ∩ (B ∪ C) = [{3,5,7,9,11} ∩{7,9,11,13}] ∩ [{7,9,11, 13} ∪ {11,13, 15}] = {7,9,11} ∩ {7,9,11,13,15} = {7,9,11}. (x)(A ∪ D) ∩ (B ∪ C) = [{3,5,7,9,11} ∪ {15,17}] ∩ [{7, 9, 11, 13} ∪ {11, 13, 15} ={3,5,7,9,11,15,17} ∩ {7,9,11,13,15} ={7,9,11,15}. |
| Q7. If A = {x : x is a natural number }, B = {x : x is an even natural number} C = {x : x is an odd natural number} and D = {x : x is a prime number }, find A
(iv) B
|
| A.7. A = {1,2,3,4,5, 6, …} B = {2,4,6, …} C = {1,3,5, …} D = {2,3,5, …,} (i)A ∩ B = {1,2,3,4 …} ∩ {2,4,6, …} = {2,4,6 …} = B. (ii)A ∩ C = {1,2,3,4, …} ∩ {1,3,5 …} = {1,3,5, …} = C. (iii)B ∩ C = {2,4,6, …} ∩ {1,3,5, …} =
(iv)B ∩ D = {2,4,6 …} ∩ {2,3,5 …} = {2} (v)C ∩ D = {1,3,5, …} ∩ {2,3,5 …} = {3,5,7 …} = {x : x is odd prime number} |
| Q.8. Which of the following pairs of sets are disjoint (i){1, 2, 3, 4} and {x : x is a natural number and
(ii) {a, e, i, o, u } and { c, d, e, f } (iii) {x : x is an even integer} and {x : x is an odd integer} |
| A.8. (i){1,2,3,4} ∩ {x : x is a natural number and 4 ≤ x ≤ 6} {1, 2, 3, 4} ∩ {4, 5, 6} {4} ≠∅ Hence, the given pair of set is not disjoint. (ii){a, e, i, o, u} ∩ {c, d, e, f} {e} ≠∅ Hence, the given pair of set is not disjoint. (iii){x: x is an even integer} ∩ {x: x is are odd integer}. =∅ As there is no integer which is both even and odd at the same time. ⸫ Given pair of set are disjoint. |
| Q9. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find (i) A – B (ii) A – C (iii) A – D (iv) B – A (v) C – A (vi) D – A (vii) B – C (viii) B – D (ix) C – B (x) D – B (xi) C – D (xii) D – C |
| A.9. (i)A – B = {3,6,9,12,15,18,21} – {4,8,12,16,20} = {3,6,9,15,18,21} (ii)A – C = {3,6,9,12,15,18,21} – {2,4,6,8,10,12,14,16} = {3,9,15,18,21} (iii)A – D = {3,6,9,12,15,18,21} – {5,10,15,20} = {3,6,9,12,18,21} (iv)B – A = {4,8,12,16,20} – {3,6,9,12,15,18,21} = {4,8,16,20} (v)C – A = {2,4,6,8,10,12,14,16} – {3,6,9,12,15,18,21} = {2,4,8,10,14,16} (vi)D – A = {5,10,15,20} – {3,6,9,12,15,18,21} ={5,10,20} (vii)B – C={4,8,12,16,20} – {2,4,6,8,10,12,14,16} ={20} (viii)B – D ={4,8,12,16,20} – {5,10,15,20} = {4,8,12,16} (ix)C – B = {2,4,6,8,10,12,14,16} – {4,8,12,16,20} = {2,6,10,14} (x)D – B = {5,10,15,20} – {4,8,12,16,20} = {5,10,15} (xi)C – D = {2,4,6,8,10,12,14,16} – {5,10,15,20} = {2,4,6,8,12,14,16} (xii)D – C = {5,10,15,20} – {2,4,6,8,10,12,14,16} = {5,15,20} |
| Q10. If X= { a, b, c, d } and Y = { f, b, d, g}, find (i)X – Y (ii)Y – X (iii) X ∩Y |
| A.10. (i)X – Y = {a, b, c, d} – (f, b, d, g} = {a, c} (ii) Y – X = {f, b, d, g} – {a, b, c, d} = {f, g} (iii)X ∩ Y = {a, b, c, d} ∩ {f, b, d, g} = {b, d}. |
| Q11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q? |
| A.11. R – Q = {x: x is a real number but not rational number} = {x: x is an irrational number} Since real number = rational number + irrational number |
| Q12. State whether each of the following statement is true or false. Justify your answer. (i) {2, 3, 4, 5} and {3, 6} are disjoint sets. (ii) {a, e, i, o, u} and {a, b, c, d}are disjoint sets. (iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets. (iv) {2, 6, 10} and {3, 7, 11} are disjoint sets. |
| A.12. (i)False, as {2,3,4,5} ∩ {3,6} = {3} ≠
(ii)False as {a, e, i, o, u} ∩ {a, b, c, d} = {a} ≠
(iii)True as {2,6,10,14} ∩ {3,7,11,15} =
(iv)True as {2,6,10} ∩ {3,7,11}=
|
Class 11 Chapter 1 Sets Exercise 1.5 Solutions
Class 11 Math Chapter 1 Sets Exercise 1.5 deals with the concept of Cartesian products of sets. The Class 11 Math Exercise 1.5 contains problems based on the idea of ordered pairs and how they form new sets through Cartesian products. Through Cartesian product and ordered pairs exercise 1.5 of class 11 Maths. Class 11 Math Exercise 1.5 consist of 7 Questions and students will find the Exercise 1.5 solution PDF here also. Students can check the complete solution of Exercise 1.5 Below
Exercise 1.5 Class 11 Maths SolutionsQ1. Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } andC = { 3, 4, 5, 6 }. Find (i) A
(v) (A
|
| A.1. (i)A
= {5,6,7,8,9} (ii)B
= {1,3,5,7,9}. (iii)(A
= {5,6,7,8,9} ∩ [U – C] [⸪ (i)] = {5,6,7,8,9} ∩ [{1,2,3,4,5,6,1,8,9} – {3,4,5,6}] = {5,6,7,8,9} ∩ {1,2,7,8,9} = {7,8,9} (iv)(A
= {5,6,7,8,9} ∩ {1,3,5,7,9} [⸪ (i) and (ii)] = {5,7,9}. (v)(A
= {1,2,3,4} = A (A
(vi)(B – C)
= {1,2,3,4,5,6,7,8,9} – {2,8} = {1,3,4, 5, 6,7,9}. |
| Q2. If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets : (i) A = {a, b, c} (ii) B = {d, e, f, g} (iii) C = {a, c, e, g} (iv) D = { f, g, h, a} |
| A.2. (i)A
= {d, e, f, g, h} (ii)B
= {a, b, c, h}. (iii)C
= {b, d, f, h} (iv)D
= {b, c, d, e} |
| Q3. Taking the set of natural numbers as the universal set, write down the complements of the following sets: (i) {x : x is an even natural number} (ii) { x : x is an odd natural number } (iii) {x : x is a positive multiple of 3} (iv) { x : x is a prime number } (v) {x : x is a natural number divisible by 3 and 5} (vi) {x : x is a perfect square } (vii) { x : x is a perfect cube} (viii) {x : x + 5 = 8 } (ix) { x : 2x + 5 = 9} (x) {x : x
|
| A.3. (i){x : x is an odd natural number} (ii){x : x is an even natural number} (iii){x : x is not a multiple of 3} (iv){x : x is a positive composite number and x = 1} (v){x : x is a natural number not divisible by 3 and 5}. (vi){x : x is not a perfect square} (vii){x : x is not a perfect cube} (viii)We have, x + 5 = 8. x = 8 – 5 = 3 x = 3 ⸫ {x : x ≠ 3, x ϵ N} (ix)We have, 2x + 5 = 9 2x = 9 – 5 2x = 4 x = 2 ⸫{x : x ϵ N and x ≠ 2} (x){x : x < 7} = {1,2,3,4,5,6} (xi)We have, 2x + 1 >10 2x >10 – 1 x >
⸫
|
| Q4. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that (i) A
|
| A.4. (i)L.H.S = (A
= {1,2,3,4,5,6,7,8,9} – [{2,4,6,8)
= {1,2,3,4,5,6,7,8,9} – {2,3,4,5,6,7,8} = {1,9} R.H.S. = A
=
= {1,3,5,7,9} ∩ {1,4,6,8,9} = {1,9} ⸫ L.H.S. = R.H.S. (A B) = A ∩ B. (ii)L.H.S. = (A ∩ B)
= {1,2,3,4,5,6,7,8,9} – [{2,4,6,8} ∩ {2,3,5,7}] = {1,2,3,4,5,6,7,8,9} – {2} = {1,3,4,5,6,7,8,9} R.H.S. = A
= [U – A]
= [{1,2,3,4,5,6,7,8,9} – {2,4,6,8}] [{1,2,3,4,5,6,7,8,9} – {2,3,5,7}] = {1,3,5,7,9}
= {1,3,4,5,6,7,8,9} ⸫ L.H.S. = R.H.S. (A ∩ B)
|
| Q5. Draw appropriate Venn diagram for each of the following : (i) (A
|
| A.5. (i)(A
(ii)A
|
| Q.6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, , what is A
|
| A.6. A
= Set of all triangle in a plane - Set of all triangle with at least the angle different from 60°. = Set of all triangle with each angle 60°. A´ = set of all equilateral triangle. |
| Q7. Fill in the blanks to make each of the following a true statement : (i) A
(iii) A
|
| A.7. (i)A
(ii)
(iii)A ∩ A
(iv)U
|
Class 11 Chapter 1 Sets Exercise 1.6 Solutions
Class 11 Math Exercise 1.6 focuses on the concept of relations through the extension of ordered pairs and cartesian products. In Exercise 1.6 Students will learn how to represent relations using roster form, set-builder form, and Cartesian products. Class 11 Sets 1.6 exercise also covers types of relations, such as reflexive, symmetric, and transitive relations. Exercise 1.6 Solutions PDF is also available on this page for all 8 Questions. Students can check the complete solution of Exercise 1.6 Below
Class 11 Sets Exercise 1.6 SolutionsQ1. If X and Y are two sets such that n( X ) = 17, n ( Y ) = 23 and n(X
|
| A.1. Given, n (X)= 17 n (Y) = 23 n(X
So, n(X
n(X
= 17 + 23 38. = 2 |
| Q2. If X and Y are two sets such that X
|
| A.2. Given, n(X
n(X) = 8.n(Y) = 15.n(X
Usingn(X
= 8 + 15 18. = 5. |
| Q3. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English? |
| A.3. Let H and E be set if people who speak Hindi and English respectively. there, n(H) = 250, people speak Hindi n(E) = 200, people speak English n(H
So, n(H
= 250 + 200 400 = 50 So, 50 people can speak both Hindi and English. |
| Q4. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩T has 11 elements, how many elements does S
|
| A.4. Given,n(S) = 21 n(T) = 32 n(S
Using, n(S
= 21 + 32 11 = 42. |
| Q5. If X and Y are two sets such that X has 40 elements, X
|
| A5. Given, n(X) = 40 n(Y
n(X
n(Y) = ? Using, n(X
60 = 40 + n(y) 10. n(Y) = 60 40 + 10 n(Y) = 30. |
| Q6. In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea? |
| A.6. Let A and B but the set of people who likes coffee and tea. Then, n(A) = 37. no. of people who like coffee n(B) = 52, no. of people who like tea. As each person likes at least one of the two drink, n(A
So using, n(A
n(A
= 37 + 52 70 = 89 70 = 19 So, 19 people likes both coffee and tea. |
| Q7. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis? |
| A.7. Let C and T be the set of people who likes cricket and tennis respectively. Then, n(C) = 40, people who likes cricket n(C
and n(C
So, n(C
65 = 40 + n(T) 10 n(T) = 35 So, 35 people likes tennis And number of people who likes tennis only and not cricket (TC) = n(T) n(C
|
| Q8. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages? |
| A.8. Let A and B be set of people who speaks Frenchand Spanish respectively. Then, n(A) = 50, people speak French n(B) = 20, people speak Spanish. n(A
So, number of people who speaks at least one of these two languages = n(A
= n(A) + n(B) n(A
= 50 + 20 10 = 60 |
Class 11 Chapter 1 Sets Miscellaneous Exercise NCERT Solutions
Class 11 Chapter 1 Sets NCERT Solution PDF: Free PDF Download
Important Formulas of Class 11 Maths Chapter 1 Sets
Class 11 Chapter 1 Sets: Key Topics, Weightage and Important formulae
Sets Chapter at a Glance – Class 11 Maths NCERT Solutions
Class 11 Sets - FAQs
Commonly asked questions
What is Sets in Mathematics?
Sets is a collection of objects or members which are distinct objects. Normally, the objects are listed within curly braces {}. Example of a set - set of vowels in English - {a, e, i, o, u). Sets class 11 includes multiple exercises on sets concepts.
According to class 11 Maths chapter 1, what is universal set U?
The universal set U includes the set of all natural numbers. It includes both the even and odd numbers. U= {1,2,3,4,5,6,7,8,9,10.}. U comprises all elements of Set A and Set B.
Is Sets Class 11 Maths chapter a difficult one?
Mathematics in Class 11 is considered tough as compared to Class 10 as it marks a notable leap in the abstractness and complexity. However, regular practice can help you to master the Maths Class 11 including the chapter 1 sets.
What is Union and Intersection in Class 11 Sets?
Union (? ) in sets means "or". It gives a set of all unique elements of two or more sets. Intersection (? ) means "and". It includes all the common elements of two or more sets.
Name different types of sets discussed in class 11.
The different types of sets covered in this chapter are - Empty Set, Singleton Set, Finite Set, Infinite Set, Equal Sets, Equivalent Sets, Subset, Proper Subset, Universal Set, Power Set, and Disjoint Sets.
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
- Relations and Functions
- Sets
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test
