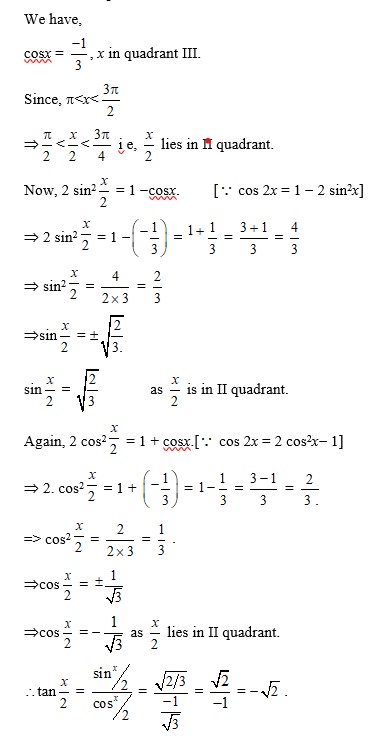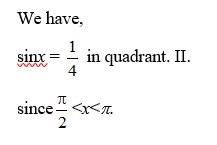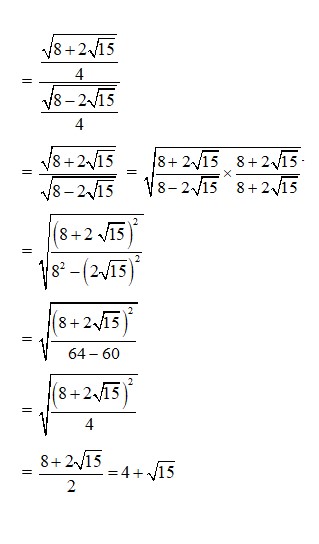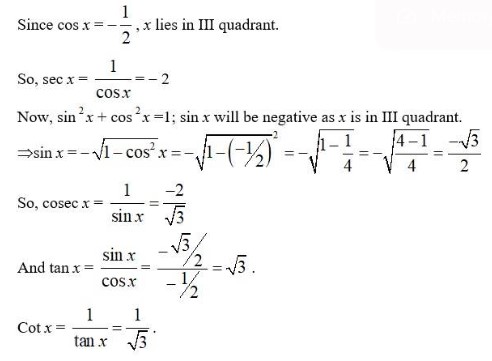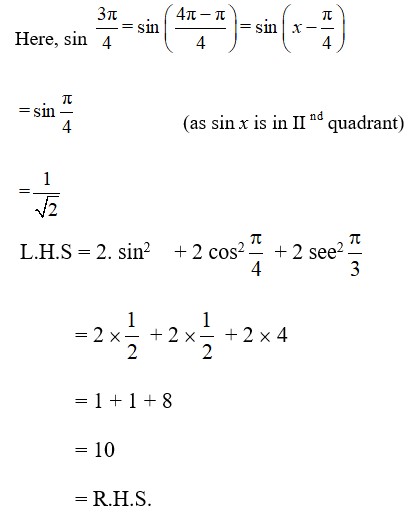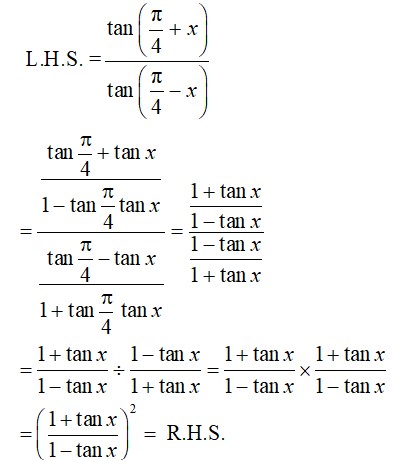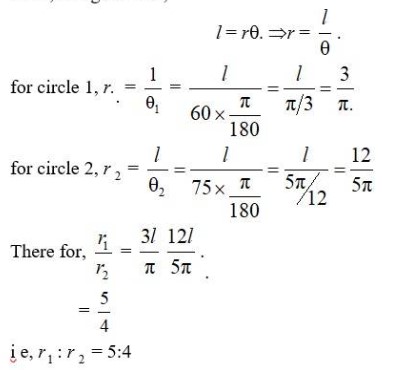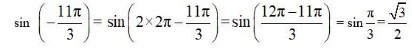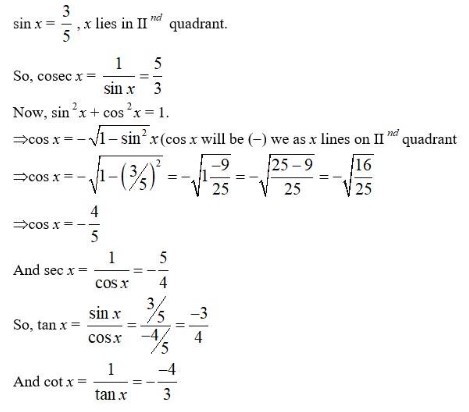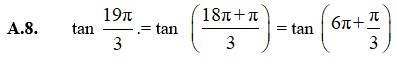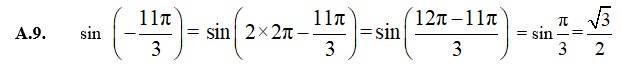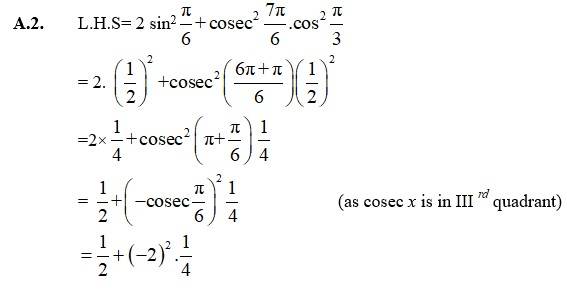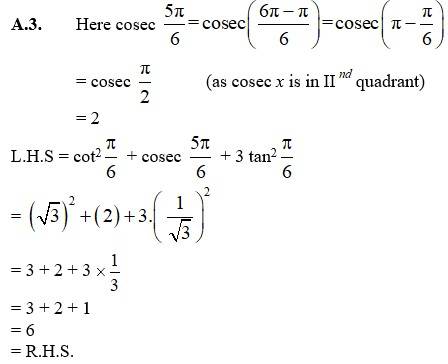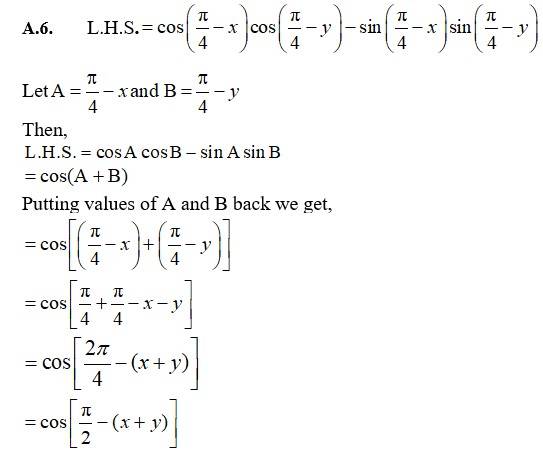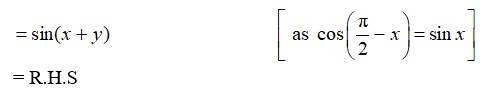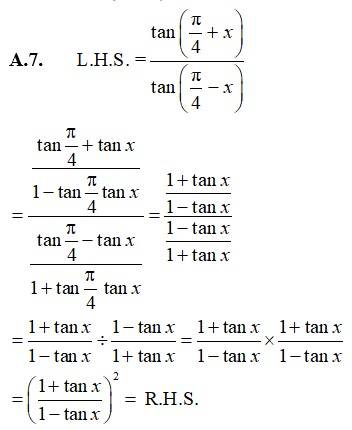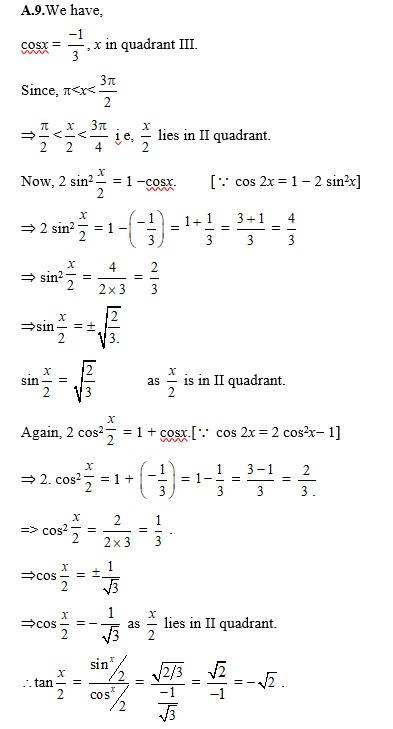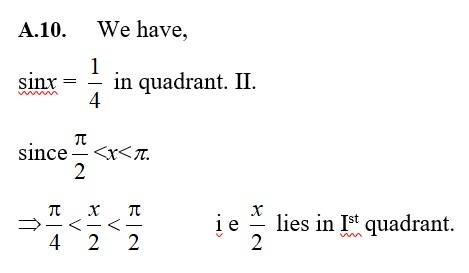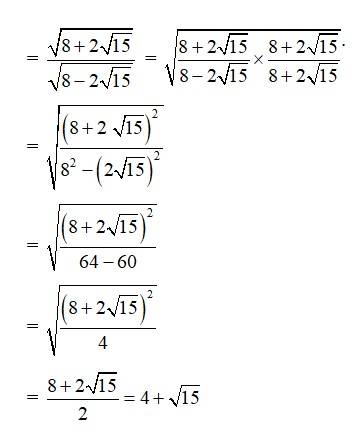29. sin26x – sin24x = sin 2x sin 10x

29. L.H.S L.H.S=sin26x−sin24x. = ( s i n 6 x + s i n 4 x ) ( s i n 6 x − s i n 4 x ) . [ a 2 − b 2 = ( a − b ) ( a + b ) ] So, L.H.S L.H.S.=(2sin(6x+4x2)cos(6x−4x2))(2cos(6x+4x2)sin(6x−4x2)) = ( 2 s i n 1 0 x 2 c o s 2 x 2 ) ( 2 c o s 1 0 x 2 s i n 2 x 2 ) = 2 s i n 5 x c o s x ⋅ 2 c o s 5 x s i n x = 2 s i n 5 x c o s 5 x ⋅ 2 c s i n x c o s x . As sin2θ=2sinθcosθ we can write. L.H.S =sin (2×5x)=sin(2×x) =sin10xsin2x= R.H.S. R.H.S

41. cos 4x = 1 – 8sin2x cos2x

41. L.H.S. = cos 4x. = cos 2 (2x) = 1 – 2 Sin2 (2x) [ cos 2x = 1 – 2 Sin2x] = 1 – 2 [2 sin xcosx]2 [ sin 2x = 2 sin xcos x] = 1 – 2 [4 sin2xcos2x] = 1 – 8 sin2xcos2x = R.H.S.

The domain of the function f(x) = c o s − 1 ( x 2 − 5 x + 6 x 2 − 9 ) l o g e ( x 2 − 3 x + 2 ) is :

[ − 1 / 2 , 1 ) ∪ ( 2 , ∞ ) − { 3 + 5 2 , 3 − 5 2 }

[ − 1 / 2 , 1 ) ∪ ( 2 , ∞ )

The domain of the function f(x) = c o s − 1 ( x 2 − 5 x + 6 x 2 − 9 ) l o g e ( x 2 − 3 x + 2 ) is :

[ − 1 / 2 , 1 ) ∪ ( 2 , ∞ ) − { 3 + 5 2 , 3 − 5 2 }

[ − 1 / 2 , 1 ) ∪ ( 2 , ∞ )

NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions

Q: Find the values of the trigonometric functions in Exercises 13 to 17. 13. sin 765°

13. sin 765° We know that value of sun x repeats after an interval of 2π or 360°. Sin (765°) = sin (2×360°+45°) = sin 45° = 1/√2.

Q: 22. Find the value of: (i) sin 75° (ii) tan 15°

22. (i) sin 75°= sin (45°+30°) Using sin (x + y)= sin x cos y + cos x sin y we can write sin 75° = sin 45°cos 30°+ 45° sin 30°

Q: 51. sin x + sin 3x + sin 5x = 0

51. We have, sinx + sin 3x + sin 5x = 0. (sinx + sin 5x) + sin 3x = 0. Using sin A + sin B = 2 sin A+B2 cos A−B2 . 2 sin (x+5x2) cos (x−5x2) + sin 3x = 0. 2 sin 6x2 cos -4x2 + sin 3x = 0. 2 sin 3xcos (-2x) + sin 3x = 0. sin 3x [2 cos 2x + 1] = 0 [ ? cos (-x) = cosx]. sin 3x = 0 or 2 cos 2x + 1 = 0. 3x = nπ, n∈z. or cos 2x = -12 = -cos π3 = cos π - π3= cos 2π3 x= nπ3 , n∈z or 2x = 2nπ± 2π3 . x = nπ± π3 , n∈z.

Updated on Jul 29, 2025 15:32 IST

By Pallavi Pathak, Assistant Manager Content

Trigonometry Class 11 Solutions deal with ‘measuring the sides of a triangle’. The term was initially developed to solve the geometric problems related to triangles. However, now it is used in many areas such as designing electric circuits, the science of seismology, predicting the heights of tides in the ocean, describing the state of an atom, analysing a musical tone, and in many other fields.
Trigonometry class 11 includes the trigonometric functions, angles, and trigonometric functions of the sum and difference of two angles. Students should go through these concepts thoroughly. It will help them to score high in the school exam, CBSE Board, and other competitive exams like the JEE Main exam.
Here, you can find the chapter-wise important topics and free PDFs of the NCERT solutions of Maths, Physics, Chemistry of Class 11 and Class 12.

Table of content

Trigonometry Class 11 NCERT Solutions Key Concepts
Class 11 Chapter 3 Trigonometric Functions: Key Topics, Weightage
Important Formulas of Trigonometry Class 11
Class 11 Chapter 3 Trigonometric Functions NCERT Solution PDF: Free PDF Download
Class 11 Chapter 3 Trigonometric Functions Exercise-wise Solution
Class 11 Chapter 3 Trigonometric Functions Exercise 3.1 Solution
Class 11 Chapter 3 Trigonometric Functions Exercise 3.2 Solution
Class 11 Chapter 3 Trigonometric Functions Exercise 3.3 Solution
Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution
Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Trigonometry Class 11 NCERT Solutions Key Concepts

Here is a walkthrough of the Class 11 Trigonometry:

In a circle, the radian measure is: $\frac{π}{180} \times Degree measure$ The degree measure is: $\frac{180}{π} \times Radian measure$ $\cos^{2} x + \sin^{2} x = 1$ $1 + \tan^{2} x = \sec^{2} x$ $1 + \cot^{2} x = {cosec}^{2} x$
$\cos (2 π + x) = \cos x$
$\sin (2 π + x) = \sin x$
$\sin (- x) = - \sin x$
$\cos (- x) = \cos x$
$\cos (x + y) = \cos x \cos y - \sin x \sin y$
$\cos (x - y) = \cos x \cos y + \sin x \sin y$
$\cos (\frac{π}{2} - x) = \sin x$

Class 11 Chapter 3 Trigonometric Functions: Key Topics, Weightage

In Trigonometry Class 11 Solutions, focus on the properties of triangles, trigonometric equations, and identities. See below the topics covered in this chapter:

Exercise	Topics Covered
3.1	Introduction
3.2	Angles
3.3	Trigonometric Functions
3.4	Trigonometric Functions of Sum and Difference of Two Angles

Trigonometry Class 11 Weightage in JEE Main Exam

Exam	Number of Questions	Weightage
JEE Main	2-3 questions	7% to 10%

Important Formulas of Trigonometry Class 11

Trigonometric Functions Important Formulae for CBSE and Competitive Exams

Reciprocal Identities:

$\csc x = \frac{1}{\sin x}, \sec x = \frac{1}{\cos x}, \cot x = \frac{1}{\tan x}$

Quotient Identities:

$\tan x = \frac{\sin x}{\cos x}, \cot x = \frac{\cos x}{\sin x}$

Pythagorean Identities:

$\sin^2 x + \cos^2 x = 1$ $1 + \tan^2 x = \sec^2 x$ $1 + \cot^{2} x = \csc^{2} x$

Trigonometric Functions of Sum and Difference of Angles

Sum and Difference Formulas: $\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$ $\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$ $\tan (A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$

Class 11 Chapter 3 Trigonometric Functions NCERT Solution PDF: Free PDF Download

To prepare well for the school examination, CBSE Board, and other entrance exams, students must study from these NCERT solutions created by Shiksha's experts. They must download the Trigonometry Class 11 NCERT PDF from the link given below.

Class 11 Chapter 3 Trigonometric Functions NCERT Solution PDF: Free PDF Download

To get access to the Class 11th Maths NCERT Solutions curated by our subject experts with important topics and weightage, check here.

Class 11 Chapter 3 Trigonometric Functions Exercise-wise Solution

Class 11 Chapter 3 Trigonometric Functions NCERT Solution PDF: Free PDF Download

Class 11 Chapter 3 Trigonometric Functions Exercise 3.1 Solution

NCERT Solutions of ex 3.1 class 11 focuses on the measurement of angles in degrees and radians, using relationship between $π$ and $180. Students will also learn to interchange$ angles in different forms and solve problems related to arc length and sector angles. The Class 11 Math exercise 3.1 also includes application-based problems involving real-life scenarios such as the motion of a wheel, and the properties of a circle’s chord. Students can check complete solution of the Trigonometric function Exercise 3.1 below;

Class 11 Chapter 3 Trigonometric Functions Ex 3.1 NCERT Solution

Q1. Find the radian measures corresponding to the following degree measures:

(i) 25° (ii) – 47°30′ (iii) 240° (iv) 520°

A.1. (i)25°

Solution:We know that 180° = π radian.

Hence, 25° = $\frac{π}{180}$ 25 radian= $\frac{5π}{36}$ radians.

(ii).47°30′

Solution: We know that 180° = π radian,

Hence, -47°30′= -47 × $\frac{1}{2}$ degree= $\frac{- 47}{2}$ × $\frac{π}{180°}$ radians.

= $- \frac{1 9π}{72}$ radians

(iii) 240°

Solution:We know that, 180°= radian.

Hence, 240°= 240× $\frac{π}{180}$ radian.

= $\frac{4π}{3}$ radian.

(iv) 520°

Solution: We know that, 180= radian.

Hence, 520°= 520°× $\frac{π}{180}$ radian.

= $\frac{2 6π}{9}$ radian.

Q2. Find the degree measures corresponding to the following radian measures $(U s e π = \frac{22}{7}) .$

(i) $\frac{11}{16}$ (ii)-4 (iii) $\frac{5 π}{3}$ (iv) $\frac{7 π}{6}$

A.2. (i) $\frac{11}{16}$

We know that radian= 180°,

Hence, $\frac{11}{16}$ radian= $\frac{11}{16}$ × $\frac{180°}{π}$ = $\frac{11}{16}$ × $\frac{180 °}{22 / 7}$ = $\frac{11}{16}$ × $\frac{7}{22}$ ×180 $°$

= ${(\frac{315}{8})}^{0}$

=39 0 $\frac{3 °}{8}$

= 39 $°$ + $\frac{3 \times 60}{8}$ minute (as 1 $°$ =60′)

=39°+22′+ ${(\frac{1}{2})}^{'}$

=39°+22′+ ${(\frac{60}{2})}^{''}$ (as 1′=60”)

=39°+22′+30”.

=39° 22′ 30”.

(ii) -4

We know that radian = 180°.

Hence: -4 radian = -4× $(\frac{180°}{π})$ = 4× $\frac{180 °}{\frac{22}{7}}$ = 4×180°× $\frac{7}{22}$ .

= - ${(\frac{2520}{11})}^{0}$

=229 0 $\frac{1 °}{11}$

=229+ $\frac{1 \times 60'}{11}$

=229+5′+ ${(\frac{5}{11})}^{'}$ .

=229°+5′+27″

=229° 5′27″

(iii) $\frac{5π}{3} .$ .

Solution: We know that, π radian= 180°.

Here $\frac{5π}{3}$ radian = $\frac{5π}{3}$ × $\frac{180°}{π}$ $\frac{}{}$ =300°

(iv) $\frac{7π}{6}$

Solution: We know that radian =180° .

Here, $\frac{7π}{6}$ radian = $\frac{7π}{6}$ × $\frac{180°}{π}$ =210°

Q3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

A.3. Given that a wheel makes 360 revolutions in one minute

Then, number of revolutions in one second = $\frac{360}{60}$ =6.

In 1 complete revolution the wheel turns 360°= 2π radian.

So, In 6 revolution, the wheel will turns 6×2π radian = 12π radian.

Hence, in one second the wheel will turn an angle of 12π radian.

Q4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm $(U s e π = \frac{22}{7}) .$

A.4. Here l = 22cm.

r =100cm.

Ø = ?

Hence by r = $\frac{1}{Ø}$

= Ø = $\frac{l}{r}$ = $\frac{22}{100}$ radian

= $\frac{22}{100}$ × $\frac{180°}{π}$

= $\frac{22}{100}$ × 180° × $\frac{7}{22}$

= ${(\frac{63}{5})}^{0}$

=12 $\frac{3 °}{5}$ = 12° $\frac{3 \times 60'}{5} = 12 ° 36'$

Q5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

So, radius, r = $\frac{40}{2}$ cm = 20 cm

Length of chord (AB) = 20cm

In OAB

OA = OB=AB=20 cm

Hence, AOAB is equilateral triangle and end of the angle is 60°

:. Ø =60° = 60 × $\frac{π}{180}$ radian = $\frac{π}{3}$ radian

Hence, length of minor are of the chord, l=rØ.

l = 20 × $\frac{π}{3}$ cm

l = $\frac{2 0π}{3}$ cm.

Q6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

Q7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length

(i) 10 cm (ii) 15 cm (iii) 21 cm

A.7. Here,

r= length of pendulum.

r= 75 cm.

(i)Are of length, l = 10 cm

Ø= $\frac{l}{r}$ = $\frac{10 c m}{75 c m} = \frac{2}{15}$ radian.

(ii) are of length, l = 15 cm.

So, Ø= $\frac{l}{r}$ = $\frac{15 c m}{75 c m} = \frac{1}{5}$ radian.

(iii) are for length, l= 21 cm.

So, Ø= $\frac{l}{r} = \frac{21 c m}{75 c m} = \frac{7}{25}$ radian.

Commonly asked questions

Find the values of the trigonometric functions in Exercises 13 to 17.

13. sin 765°

13. sin 765°

We know that value of sun x repeats after an interval of 2π or 360°.

Sin (765°) = sin (2×360°+45°)

= sin 45°

= 1/√2.

22. Find the value of:

(i) sin 75° (ii) tan 15°

22. (i) sin 75°= sin (45°+30°)

Using sin (x + y)= sin x cos y + cos x sin y we can write

sin 75°

= sin 45°cos 30°+ 45° sin 30°

29. sin²6x – sin²4x = sin 2x sin 10x

29. L.H.S $L.H.S = s i n^{2} 6 x - s i n^{2} 4 x .$

$= (s i n 6 x + s i n 4 x) (s i n 6 x - s i n 4 x) . [a^{2} - b^{2} = (a - b) (a + b)]$

So, L.H.S $L.H.S. = (2 s i n (\frac{6 x + 4 x}{2}) c o s (\frac{6 x - 4 x}{2})) (2 c o s (\frac{6 x + 4 x}{2}) s i n (\frac{6 x - 4 x}{2}))$

$= (2 s i n \frac{10 x}{2} c o s \frac{2 x}{2}) (2 c o s \frac{10 x}{2} s i n \frac{2 x}{2})$

$= 2 s i n 5 x c o s x \cdot 2 c o s 5 x s i n x$

$= 2 s i n 5 x c o s 5 x \cdot 2 c s i n x c o s x .$

As $s i n 2 θ = 2 s i n θ c o s θ$ we can write.

$L.H.S = s i n (2 \times 5 x) = s i n (2 \times x)$

$= s i n 10 x s i n 2 x = R.H.S.$ R.H.S

51. sin x + sin 3x + sin 5x = 0

51. We have,

sinx + sin 3x + sin 5x = 0.

(sinx + sin 5x) + sin 3x = 0.

Using sin A + sin B = 2 sin $\frac{A+B}{2}$ cos $\frac{A-B}{2}$ .

2 sin $(\frac{x + 5 x}{2})$ cos $(\frac{x - 5 x}{2})$ + sin 3x = 0.

2 sin $\frac{6 x}{2}$ cos $\frac{-4 x}{2}$ + sin 3x = 0.

2 sin 3xcos (-2x) + sin 3x = 0.

sin 3x [2 cos 2x + 1] = 0 [ $?$ cos (-x) = cosx].

sin 3x = 0 or 2 cos 2x + 1 = 0.

3x = nπ, n∈z. or cos 2x = $\frac{-1}{2}$ = -cos $\frac{π}{3}$ = cos π - $\frac{π}{3}$ = cos $\frac{2 π}{3}$

x= $\frac{n π}{3}$ , n∈z or 2x = 2nπ± $\frac{2 π}{3}$ .

x = nπ± $\frac{π}{3}$ , n∈z.

41. cos 4x = 1 – 8sin²x cos²x

41. L.H.S. = cos 4x.

= cos 2 (2x)

= 1 – 2 Sin² (2x) [ cos 2x = 1 – 2 Sin²x]

= 1 – 2 [2 sin xcosx]² [ sin 2x = 2 sin xcos x]

= 1 – 2 [4 sin²xcos²x]

= 1 – 8 sin²xcos²x

= R.H.S.

42. cos 6x = 32 cos⁶x – 48cos⁴x + 18 cos²x – 1

42. L.H.S. = cos 6x

= cos 3 (2x)

= 4 cos³2x – 3 cos 2x [Q cos 3A = 4 cos³A – 3cos A]

= 4 [ (2 cos²x – 1)³] – 3 [ (2 cos²x – 1)] [Q cos 2x = 2 cos²x – 1]

= 4 [ (2 cos²x)³ + 3 [ (2 cos²x)² (–1) + 3 (2 cos²x) (–1)² + (–1)³] – 3 (2 cos²x) + 3

{Q (a + b)³= a³ + b³ + 3a²b + 3ab²}

= 4 [8 cos⁶x – 12 cos⁴x + 6cos²x – 1] – 6 cos²x + 3.

= 32 cos⁶x – 48 cos⁴x + 24 cos²x – 4 – 6cos²x + 3

= 32 cos⁶x – 48 cos⁴x + 18 cos²x – 1

= R.H.S.

57. $\frac{(s i n 7 x + s i n 5 x) + (s i n 9 x + s i n 3 x)}{(c o s 7 x + c o s 5 x) + (c o s 9 x + c o s 3 x)} = t a n 6 x$

57. L.H.S. = $\frac{(s i n 7 x + s i n 5 x) + (s i n 9 x + s i n 3 x)}{(c o s 7 x + c o s 5 x) + (c o s 9 x + c o s 3 x)} .$

Using sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A - B}{2}$

cos A + cos B = 2 cos $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

48. cos 3x + cos x – cos 2x = 0

48. We have,

cos 3x + cosx-cos 2x = 0.

(cos 3x + cosx) cos 2x = 0

Using cos A + cos B = 2 cos $\frac{A+B}{2}$ cos $\frac{A-B}{2}$

2 cos $(\frac{3 x + x}{2})$ cos $(\frac{3 x - x}{2})$ - cos 2x = 0.

2 cos $\frac{4 x}{2}$ cos $\frac{2 x}{2}$ - cos 2x = 0

2 cos 2xcosx - cos 2x = 0

cos 2x. (2 cosx - 1) = 0.

cos 2x = 0 or 2 cosx -1 = 0.

2x = (2n + 1) $\frac{π}{2}$ , n∈z or cosx = $\frac{1}{2}$ = cos $\frac{π}{3}$

x = (2n + 1) $\frac{π}{4}$ , n∈z or x = 2nx± $\frac{π}{3}$ , n∈z.

46. cosec x = – 2

46. We have cosec x = 2 .i e, cosec x = (-)ve,

So, the principal solution lies in IIInd and IVth quadrent.

Now, cosec x = -2 = -cosec $\frac{π}{6}$ = cosec $(π + \frac{π}{6}$ = cosec $(2 π - \frac{π}{6})$

So the principal solution are x = $(π + \frac{π}{6})$ and $(2 π - \frac{π}{6})$

= $(\frac{6 π + π}{6})$ and $(\frac{12 π - π}{6})$

= $\frac{7 π}{6}$ and $\frac{11 π}{6} .$

As cosec x = cosec $\frac{7 π}{6}$ ⇒sin x = sin $\frac{7 π}{c}$ $[? c o s e c x = \frac{1}{s i n x}]$

The general solution has the form,

x = nπ + (-1)n $\frac{7 π}{6}$ , n∈z.

49. sin 2x + cos x = 0

49. We have,

sin 2x + cosx = 0.

2 sin cosx + cosx = 0 ( $?$ sin 2x = 2 sin xcosx)

cosx (2 sin x + 1) = 0.

cosx = 0 or 2 sinx + 1 = 0.

x = (2n + 1) $\frac{π}{2}$ , n∈z or sin x = $\frac{1}{2}$ = -sin $\frac{π}{6}$ = sin π + $\frac{π}{6}$ = sin $\frac{7 π}{6} .$

x = (2n + 1) $\frac{π}{2}$ , x∈z or x= nπ + (-1)ⁿ $\frac{7 π}{6},$ n∈z.

Find the general solution for each of the following equations:

47. cos 4 x = cos 2 x

47. We have,

cos 4x = cos 2x.

⇒ cos 4x-cos 2x = 0.

⇒ -2 sin $(\frac{4 x + 2 x}{2})$ sin $(\frac{4 x - 2 x}{2})$ = 0.

⇒sin $\frac{6 x}{2}$ sin $\frac{2 x}{2}$ = 0

⇒sin 3x sin x = 0.

∴sin 3x = 0 or sin x = 0

3x = nπ or x = nπ, n∈z,

⇒x = $\frac{n π}{3}$ or x = nπ, n∈z

50. sec²2x = 1– tan 2x

50. We have,

sec² 2x = 1 tan 2x

1 + tan² 2x = 1 tan 2x [ sec²x = 1 + tan²x]

tan² 2x + tan 2x = 0.

tan 2x (tan 2x + 1) = 0.

tan 2x = 0 or tan 2x + 1 = 0.

2x = nπ, x∈z or tan 2x = -1 = -tan $\frac{π}{4}$ = tan π- $\frac{π}{4}$ = tan $\frac{3 π}{4} .$

x= $\frac{n π}{2}$ , n∈z or 2x = nπ + $\frac{3 π}{4}$ , n∈z.

x = $\frac{n π}{2} + \frac{3 π}{8},$ n∈z

38. $\frac{c o s 4 x + c o s 3 x + c o s 2 x}{s i n 4 x + s i n 3 x + s i n 2 x} = c o t 3 x$

38. L.H.S $= \frac{c o s 4 x + c o s 3 x + c o s 2 x}{s i n 4 x + s i n 3 x + s i n 2 x .}$

$= \frac{(c o s 4 x + c o s 2 x) + c o s 3 x}{(s i n 4 x + s i n 2 x) + s i n 3 x} .$

$= \frac{2 c o s (\frac{4 x + 2 x}{2}) c o s (\frac{4 x - 2 x}{2}) + c o s 3 x}{2 s i n (\frac{4 x + 2 x}{2}) c o s (\frac{4 x - 2 x}{2}) s i n 3 x} .$

$= \frac{2 c o s \frac{6 x}{2} c o s \frac{2 x}{2} + c o s 3 x}{2 s i n \frac{6 x}{2} c o s \frac{2 x}{2} + s i n 3 x}$

$= \frac{2 c o s 3 x c o s x + c o s 3 x}{2 s i n 3 x c o s x + 3 x}$

$= \frac{c o s 3 x}{s i n 3 x} \times \frac{(2 c o s x + 1)}{(2 c o s x + 1)}$

$= c o t 3 x =R.H.S$

34. $\frac{s i n 5 x + s i n 3 x}{c o s 5 x + c o s 3 x} = t a n 4 x$

34. $= \frac{s i n 5 x + s i n 3 x}{c o s 5 x + c o s 3 x .}$

$= \frac{2 s i n (\frac{5 x + 3 x}{2}) c o s (\frac{5 x - 3 x}{2})}{2 c o s (\frac{5 x + 3 x}{2}) c o s (\frac{5 x - 3 x}{2})}$

$= \frac{s i n \frac{8 x}{2} c o s \frac{2 x}{2}}{c o s \frac{8 x}{2} c o s \frac{2 x}{2}}$

$= \frac{s i n 4 x}{c o s 4 x} = t a n 4 x =$ R.H.S

25. Kindly Consider the following

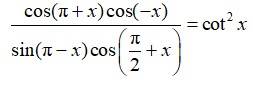
$28.$ $c o s (\frac{3 π}{4} + x) - c o s (\frac{3 π}{4} - x) = -\sqrt2 s i n x$

$28.$ L.H.S = $L.H.S = c o s (\frac{3 π}{4} + x) - c o s (\frac{3 π}{4} - x)$

Using cos (A + B) = cos A cos B – sin A sin B

and cos (A – B) = cos A cos B + sin A sin B

$L.H.S = [c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x] - [c o s \frac{3 π}{4} c o s x + s i n \frac{3 π}{4} s i n x]$

$= c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x - c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x .$

$= - 2 s i n \frac{3 π}{4} s i n x .$

$= - 2 s i n (\frac{4 π - π}{4}) s i n x .$

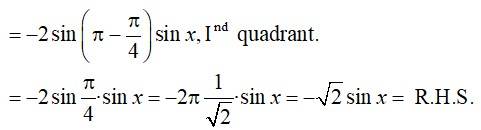
35. $\frac{s i n x - s i n y}{c o s x + c o s y} = t a n \frac{x - y}{2}$

35. L.H.S: = $L.H. S: = \frac{s i n x - s i n y}{c o s x + c o s y}$

$= \frac{2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}}{2 c o s \frac{x + y}{2} c o s \frac{x - y}{2}}$

$= \frac{s i n (\frac{x - y}{2})}{c o s (\frac{x - y}{2})}$

$= t a n (\frac{x - y}{2}) = R.H.S.$ = R.H.S.

58. sin 3x + sin 2x – sin x = 4sin x $c o s \frac{x}{2} c o s \frac{3 x}{2}$

58. L.H.S = sin 3x + sin 2x - sin x

= sin 3x - sin x + sin 2x.

= 2 cos $\frac{3 x + x}{2}$ .. sin $\frac{3 x - x}{2}$ + sin 2x $[? s i n A - s i n B = 2 c o s \frac{A + B}{2} s i n \frac{A - B}{2}]$

= 2 cos $\frac{4 x}{2}$ sin $\frac{2 x}{2}$ + sin 2x.

= 2 cos 2x sin x + 2 sin xcosx [ $?$ sin 2x = 2sin xcosx]

= 2 sin x [cos 2x + cosx]

= 2 sin x $[2 c o s \frac{2 x + x}{2} c o s \frac{2 x - x}{2}]$ $[? c o s A + c o s B = 2 c o s \frac{A + B}{2} c o s \frac{A - B}{2}]$

= 2 sin x $[2 . c o s \frac{3 x}{2} c o s \frac{x}{2}]$

= 4 sin xcos $\frac{x}{2}$ . cos $\frac{3 x}{2}$ = R.H.S.

12. tan x = –5/12, x lies in second quadrant.

12. Kindly go through the solution

37. $\frac{s i n x - s i n 3 x}{s i n^{2} x - c o s^{2} x} = 2 s i n x$

37. $= \frac{s i n x - s i n 3 x}{s i n^{2} x - c o s^{2} x}$

$= \frac{2 c o s (\frac{x + 3 x}{2}) s i n \frac{x - 3 x}{2}}{- (c o s^{2} x - s i n^{2} x)}$

$= \frac{2 c o s \frac{4 x}{2} s i n (- \frac{2 x}{2})}{- c o s 2 x} [? c o s 2 x = c o s^{2} x - s i n^{2} x]$

$= - \frac{2 c o s 2 x s i n x}{- c o s 2 x} [? s i n (- x) = - s i n x]$

= 2 sin x

= R.H.S.

60. cos x = −1/3, x in quadrant III

60. Kindly go through the solution

61. sin x = 1/4 in quadrant II

61. Kindly go through the solution

19. $2 S i n^{2} \frac{π}{6} + c o s e c^{2} \frac{7 π}{6} c o s^{2} \frac{π}{3} = \frac{3}{2}$

19.

$= \frac{1}{2} + 4 . \frac{1}{4}$

$= \frac{1}{2} + 1$ $= \frac{3}{2}$

= R.H.S.

36. $\frac{s i n x + s i n 3 x}{c o s x + c o s 3 x} = t a n 2 x$

36. $= \frac{s i n x + s i n 3 x}{c o s x + c o s 3 x}$

$= \frac{2 (\frac{x + 3 x}{2}) c o s (\frac{x - 3 x}{2})}{2 c o s (\frac{x + 3 x}{2}) c o s (\frac{x - 3 x}{2})}$

$= \frac{s i n \frac{4 x}{2}}{c o s \frac{4 x}{2}}$

$= \frac{s i n 2 x}{c o s 2 x}$

$= t a n 2 x =$ R.H.S

44. Kindly consider the following Secx = 2

44. Secx = 2. .

We have, Secx = 2, | Secx is (+)ve the principal solution lies in I^st and IV^thquadrent.

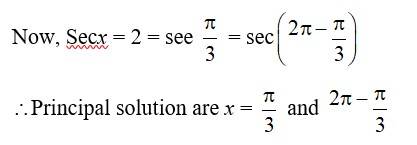
= $\frac{π}{3}$ and $\frac{6 π - π}{3}$

= $\frac{π}{3}$ and $\frac{5π}{3}$ .

As secx = sec $\frac{π}{3}$ . cosx = cos $\frac{π}{3}$ $[∴ s e c x = \frac{1}{c o s x}]$

The general solution is

x = 2nπ ± $\frac{π}{3}$ , n ∈ z.

Class 11 Trigonometric Functions Exercise 3.2 Solution

Find the values of other five trigonometric functions in Exercises 8 to 12.

8. cos x = –1/2 , x lies in third quadrant.

8. Kindly go through the solution

20. $c o t^{2} \frac{π}{6} + c o s e c \frac{5 π}{6} + 3 t a n^{2} \frac{π}{6} = 6$

5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

5. Given, diameter of circle = 40 cm

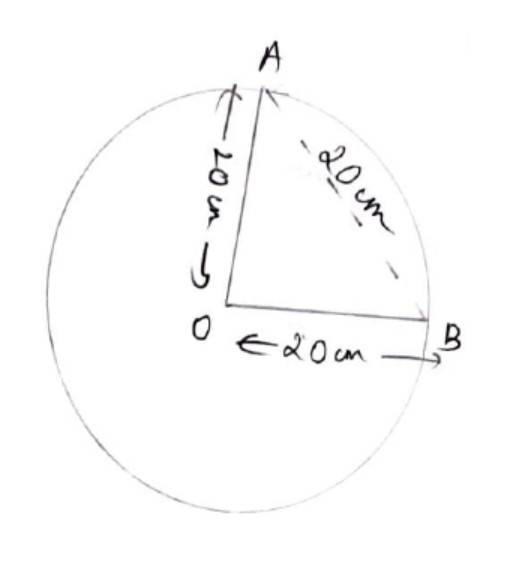
So, radius, r = $\frac{40}{2}$ cm = 20 cm

Length of chord (AB) = 20cm

In OAB

OA = OB=AB=20 cm

Hence, AOAB is equilateral triangle and end of the angle is 60°

:. Ø =60° = 60 ×
$\frac{π}{180}$ radian = $\frac{π}{3}$ radian

Hence, length of minor are of the chord, l=rØ.

l = 20 × $\frac{π}{3}$ cm

l = $\frac{2 0π}{3}$ cm.

26. $c o s (\frac{3 π}{2} + x) c o s (2 π + x) [c o t (\frac{3 π}{2} - x) + c o t (2 π + x)] = 1$

26. L.H.S $L.H.S. = c o s (\frac{3 π}{2} + x) c o s (2 π + x) [c o t (\frac{3 π}{2} - x) + c o t (2 π + x)]$

Here,

$c o s (\frac{3 π}{2} + x) = c o s (\frac{4 π - π}{2} + x) = c o s (2 π - \frac{π}{2} + x)$

$= c o s [2 π - (\frac{π}{2} - x)]; VI quadrant.$

$c o s (\frac{π}{2} - x); i I^{st} quadrant.$

$= s i n x$

$c o s (2 x + x) = c o s x, as x lies in I^{st} quadrant.$

$c o t (2 π + x) = c o t x; as x lies in I^{st} quadrant.$

$c o t (\frac{3 π}{2} - x) = c o t [\frac{4 π - π}{2} - x]$

$= c o t [2 π - \frac{π}{2} - x]$

$= c o t [2 x - (\frac{π}{2} + x)]; V I^{th} quadrant.$

$= - c o t (\frac{π}{2} + x); I I^{nd} quadrat.$

$= - (- t a n x)$

$= t a n x .$

So.L.H.S $L.H.S = s i n x c o s x [t a n x + c o t x]$

$= s i n x c o s x [\frac{s i n x}{c o s x} + \frac{c o s x}{s i n x}]$

$= s i n x c o s x \frac{(s i n^{2} x + c o s^{2} x)}{c o s x s i n x}$

$= s i n^{2} x + c o s^{2} x$

= 1

= R.H.S.

31. sin2 x + 2 sin 4x + sin 6x = 4 cos²x sin 4x

31. L.H.S. = sin 2x + 2 sin 4x + sin 6x

Using sin A + sin B = 2 sin A + B/2 cos A - B/2 we have,

L.H.S. = (sin 2x + sin 6x) + 2 sin 4x

$= 2 s i n (\frac{2 x + 6 x}{2}) c o s (\frac{2 x - 6 x}{2}) + 2 s i n 4 x .$

$= 2 s i n \frac{8 x}{2} c o s (- \frac{4 x}{2}) + 2 s i n 4 x .$

$= 2 s i n 4 x c o s 2 x + 2 s i n 4 x [? c o s (- x) = x]$

$= 2 s i n 4 x [c o s 2 x + 1]$

We know that,

$c o s 2 x = 2 c o s^{2} x - 1$

$\Rightarrow c o s 2 x + 1 = 2 c o s^{2} x$

Hence,

L.H.S $= 2 s i n 4 x (2 c o s^{2} x)$

$= 4 c o s^{2} x s i n 4 x$

= R.H.S

33. $\frac{c o s 9 x - c o s 5 x}{s i n 17 x - s i n 3 x} = - \frac{s i n 2 x}{c o s 10 x}$

33. $= \frac{c o s 9 x - c o s 5 x}{s i n 17 x - s i n 3 x}$

$= \frac{- 2 s i n (\frac{9 x + 5 x}{2}) s i n (\frac{9 x - 5 x}{2})}{2 c o s (\frac{17 x + 3 x}{2}) s i n (\frac{17 x - 3 x}{2})}$

$= \frac{- s i n \frac{14 x}{2} s i n \frac{4 x}{2}}{c o s \frac{20 x}{2} s i n \frac{14 x}{2}} = \frac{- s i n 7 x s i n 2 x}{c o s 10 x s i n 7 x} = \frac{- s i n 2 x}{c o s 10 x}$

= R.H.S

40. $t a n 4 x = \frac{4 t a n x (1 - t a n^{2} x)}{1 - 6 t a n^{2} x + t a n^{4} x}$

40. L.H.S. = tan 4x

We know that,

$t a n 2 = \frac{2 t a n}{1 - t a n^{2}} .$ , we can write

$L.H.S= t a n 2 (2 x) = \frac{2 t a n 2 x}{1 - t a n^{2} 2 x .}$

$= \frac{2 (\frac{2 t a n x}{1 - t a n^{2} x})}{1 - {(\frac{2 t a n x}{1 - t a n^{2} x})}^{2}}$

$= \frac{\frac{4 t a n x}{(1 - t a n^{2} x)}}{\frac{{(1 - t a n^{2} x)}^{2} - 4 t a n^{2} x}{{(1 - t a n^{2} x)}^{2}}}$

$= \frac{4 t a n x \times (1 - t a n^{2} x)}{1 + t a n^{4} x - 2 t a n^{2} x - 4 t a n^{2} x}$

$= \frac{4 t a n x (1 - t a n^{2} x)}{1 - 6 t a n^{2} x + t a n^{4} x}$

= R.H.S.

30. cos²2x – cos²6x = sin 4x sin 8x

30. L.H.S $L.H.S = c o s^{2} 2 x - c o s^{2} 6 x$

$= (c o s 2 x + c o s 6 x) (c o s 2 x - c o s 6 x) [? a^{2} - b^{2} = (a - b) (a + b)]$

L.H.S =

L.H.S = [2 c o s (\frac{2 x + 6 x}{2}) c o s (\frac{2 x - 6 x}{2})] [- 2 s i n \frac{2 x + 6 x}{2} s i n (\frac{2 x - 6 x}{2})]

= [2 c o s \frac{8 x}{2} c o s (- \frac{4 x}{2})] [- 2 s i n (\frac{8 x}{2}) s i n (- \frac{4 x}{2})]

= 2 c o s 4 x c o s 2 x \times 2 s i n 4 x \cdot s i n 2 x [? c o s (- x) = c o s x; s i n (- x) = - s i n x]

= 2 s i n 4 x c o s 4 x \times 2 s i n 2 x c o s 2 x

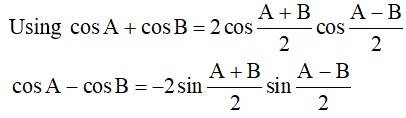
As sin 2θ = 2 sinθ cosθ.

L.H.S. = sin (2*4x) sin(2*2x)

= sin 8x sin 4x

= R.H.S.

Find sin $\frac{x}{2}$ , cos $\frac{x}{2}$ and tan $\frac{x}{2}$ in each of the following :

59. tan x = − $\frac{4}{3}$ , x in quadrant II

59. We have, tan x= $\frac{- 4}{3}$ , x in IInd quadrant.

Since, $\frac{π}{2} < x < π$

$\frac{π}{4} < \frac{x}{2} < \frac{π}{2}$

sin $\frac{x}{2}$ , cos $\frac{x}{2}$ , tan $\frac{x}{2}$ are all positive.

Now, sec²x = 1 + tan²x = 1 + ${(\frac{- 4}{3})}^{2}$ = 1 + $\frac{16}{9}$ = $\frac{9 + 16}{9}$ = $\frac{25}{9}$

secx = ± $\frac{5}{3}$

cosx = ± $\frac{3}{5}$ .

cosx = $\frac{- 3}{5}$ as x is in IInd quadrant.

Now, 2 sin².. = 1 cosx. [cos 2x = 1 2 sin²x.]

2 sin² $\frac{x}{2}$ = 1 $(\frac{- 3}{5})$

2 sin² $\frac{x}{2}$ = 1 + $\frac{3}{5}$ = $\frac{5 + 3}{5}$ = $\frac{8}{5}$ .

sin² $\frac{x}{2}$ = $\frac{8}{2 \times 5}$ = $\frac{4}{5 .}$

45. cot x = -√3

45. We have, cot x = -√3 i.e., cot x is negative

So, the principal solution lies in II^nd and IV^th quadrant.

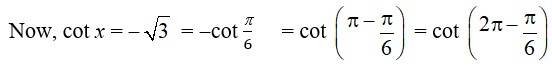
So the principal solution are a = $(π - \frac{π}{6})$ and $(2 π - \frac{π}{6})$

= $(\frac{6 π - π}{6})$ and $(\frac{12 π - π}{6})$

= $\frac{5 π}{6}$ and $\frac{11 π}{6} .$

As cot x = cot $\frac{5 π}{6}$ tan x = tan $\frac{5 π}{6}$ $[? c o t x = \frac{1}{t a n x}]$

The general solution has the form.

x = n+ $\frac{5 π}{6}$ , nz

Class 11 Chapter 3 Trigonometric Functions Ex 3.1 NCERT Solution

1. Find the radian measures corresponding to the following degree measures:

(i) 25° (ii) – 47°30′ (iii) 240° (iv) 520°

1. (i) 25°

Solution:We know that 180° = π radian.

Hence, 25° = $\frac{π}{180}$ 25 radian= $\frac{5π}{36}$ radians.

(ii) 47°30′

Solution: We know that 180° = π radian,

Hence, -47°30′= -47 × $\frac{1}{2}$ degree= $\frac{- 47}{2}$ × $\frac{π}{180°}$ radians.

= $- \frac{1 9π}{72}$ radians

(iii) 240°

Solution:We know that, 180°= radian.

Hence, 240°= 240× $\frac{π}{180}$ radian.

= $\frac{4π}{3}$ radian.

(iv) 520°

Solution: We know that, 180= radian.

Hence, 520°= 520°× $\frac{π}{180}$ radian.

= $\frac{2 6π}{9}$ radian.

4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm $(U s e π = \frac{22}{7}) .$

4. Here l = 22cm.

r =100cm.

Ø =?

Hence by r = $\frac{1}{Ø}$

= Ø = $\frac{l}{r}$ = $\frac{22}{100}$ radian

= $\frac{22}{100}$ × $180°$ /π

= $\frac{22}{100}$ × 180° × $\frac{7}{22}$

= ${(\frac{63}{5})}^{0}$

=12 $\frac{3 °}{5}$ = 12° $\frac{3 \times 60'}{5} = 12 ° 36'$

7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length

(i) 10 cm (ii) 15 cm (iii) 21 cm

7. Here,

r= length of pendulum.

r= 75 cm.

(i) Arc of length, l = 10 cm

Ø= $\frac{l}{r}$ = $\frac{10 c m}{75 c m} = \frac{2}{15}$ radian.

(ii) Arc of length, l = 15 cm.

So, Ø= $\frac{l}{r}$ = $\frac{15 c m}{75 c m} = \frac{1}{5}$ radian.

(iii) Arc for length, l= 21 cm.

So, Ø= $\frac{l}{r} = \frac{21 c m}{75 c m} = \frac{7}{25}$ radian.

53. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0

53. L.H.S = (sin 3x + sin x) + sin x + (cos 3x - cosx) cosx.

Using

Sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A-B}{2}$

cos A - cos B = -2 sin $\frac{A+B}{2}$ sin $\frac{A-B}{2}$ .

L.H.S. = $(2 s i n \frac{3 x + x}{2} c o s \frac{3 x - x}{2})$ sin x + $(- 2 s i n \frac{3 x + x}{2} s i n \frac{3 x - x}{2})$ cosx

= 2 sin $\frac{4 x}{2}$ cos $\frac{2 x}{2}$ sin x -2 sin $\frac{4 x}{2}$ sin $\frac{2 x}{2}$ cosx.

= 2 sin 2xcosx sin x -2 sin 2x sin xcosx

= 0 = R.H.S.

21. $2 s i n^{2} \frac{3 π}{4} + 2 c o s^{2} \frac{π}{4} + 2 s e c^{2} \frac{π}{3} = 10$

24. $\frac{t a n (\frac{π}{4} + x)}{t a n (\frac{π}{4} - x)} = {(\frac{1 + t a n x}{1 - t a n x})}^{2}$

6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

6. Let r₁ and r₂ be the radii of two circles.

Then using relation

2. Find the degree measures corresponding to the following radian measures $(U s e π = \frac{22}{7}) .$

(i) $\frac{11}{16}$ (ii)-4 (iii) $\frac{5 π}{3}$ (iv) $\frac{7 π}{6}$

2. (i) $\frac{11}{16}$

We know that radian= 180°,

Hence, $\frac{11}{16}$ radian= $\frac{11}{16}$ ×
$\frac{180°}{π}$ = $\frac{11}{16}$ × $\frac{180 °}{22 / 7}$ = $\frac{11}{16}$ × $\frac{7}{22}$ ×180 $°$

= ${(\frac{315}{8})}^{0}$

=39 0 $\frac{3 °}{8}$

= 39 $°$ + $\frac{3 \times 60}{8}$ minute (as 1 $°$ =60′)

=39°+22′+ ${(\frac{1}{2})}^{'}$

=39°+22′+ ${(\frac{60}{2})}^{''}$ (as 1′=60”)

=39°+22′+30”.

=39° 22′ 30”.

(ii) -4

We know that radian = 180°.

Hence: -4 radian = -4× $(\frac{180°}{π})$ = 4× $\frac{180 °}{\frac{22}{7}}$ = 4×180°× $\frac{7}{22}$ .

= - ${(\frac{2520}{11})}^{0}$

=229 0 $\frac{1 °}{11}$

=229+ $\frac{1 \times 60'}{11}$

=229+5′+ ${(\frac{5}{11})}^{'}$ .

=229°+5′+27″

=229° 5′27″

(iii) $\frac{5π}{3} .$ .

Solution: We know that, π radian= 180°.

Here $\frac{5π}{3}$ radian = $\frac{5π}{3}$ × $\frac{180°}{π}$

=300°

(iv) $\frac{7π}{6}$

Solution: We know that radian =180° .

Here, $\frac{7π}{6}$ radian = $\frac{7π}{6}$ × $\frac{180°}{π}$ =210°

16. $s i n (- \frac{11 π}{3})$

16. Kindly go through the solution

14. cosec (-1410°)

14. cosec (- 1410°)

As value of cosec x repeats after interval of 2π or 360°

∴ cosec (-1410°) = cosec (4×360°-1410°)

=cosec (1440°-1410°)

= cosec 30°

= 2.

17. $c o t (- \frac{15 π}{4})$

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

52. $2 c o s \frac{π}{13} c o s \frac{9 π}{13} + c o s \frac{3 π}{13} + c o s \frac{5 π}{13} = 0$

52. L.H.S. = 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + cos $\frac{3 π}{13}$ + cos $\frac{5 π}{13}$ =∂ .

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2 cos $\begin{array}{l} (\frac{3 π}{13} + \frac{5 π}{13}) \\ \bar{2} \end{array}$ cos $\frac{(\frac{3 π}{13} - \frac{5 π}{13})}{2}$

$[? c o s A + c o s B = 2 c o s \frac{A + B}{2} c o s \frac{A - B}{2}]$

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2. cos $(\frac{8 π / 13}{2})$ cos $(\frac{- 2 π / 13}{2})$

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2 cos $\frac{4 π}{13}$ cos $\frac{π}{13}$ [ $?$ cos (x) = cosx].

= 2 cos $\frac{π}{13}$ $[c o s \frac{9 π}{13} + c o s \frac{4 π}{13}] .$

= 2 cos $\frac{π}{13} [2 \cdot c o s (\frac{\frac{9 π}{13} + \frac{4 π}{13}}{2}) c o s (\frac{\frac{9 π}{13} - \frac{4 π}{13}}{2})]$

= 2 cos $\frac{π}{13}$ $[2 \cdot c o s (\frac{13 π / 13}{2}) c o s (\frac{5 π / 13}{2})]$

= 2 cos $\frac{π}{3}$ × 2 ×cos $\frac{π}{2}$ × cos $\frac{5 π}{26}$ .

= 2 cos $\frac{π}{2}$ 2× 0×cos $\frac{5 π}{26}$

= 0

= R.H.S.

39. cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1

39. L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x.

= cot x cot 2x – cot 3x (cot 2x + cot x)

= cot x cot 2x – (cot 2x + cot x) [cot (2x + x)]

We know that,

$c o t (A +B) = \frac{c o tA c o tB - 1}{c o tA + c o tB}$ we can write

$L.H.S= c o t x c o t 2 x - (c o t 2 x + c o t x) [\frac{c o t 2 x \cdot c o t x - 1}{c o t 2 x + c o t x}]$

= cot x cot 2x – cot 2x cot x + 1

= R.H.S.

32. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

32. L.H.S $= c o t 4 x (s i n 5 x + s i n 3 x)$

$= c o t 4 x [2 s i n \frac{8 x}{2} c o s \frac{2 x}{2}]$

$= \frac{c o s 4 x}{4 x} \times 2 s i n 4 x c o s x$

$= 2 \cdot c o s 4 x \cdot c o s x$

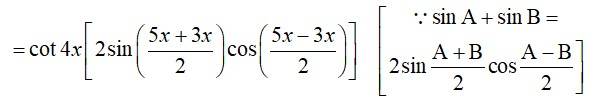
R.H.S $= c o t x [s i n 5 x - s i n 3 x]$

$= c o t x [2 c o s \frac{8 x}{2} \cdot s i n \frac{2 x}{2}]$

$= \frac{c o s x}{s i n x} \cdot 2 c o s 4 x s i n x$

$= 2 \cdot c o s 4 x \cdot c o s x .$

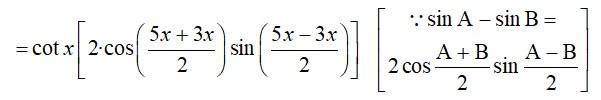
Hence, L.H.S. = R.H.S.

Prove the following:

23. $c o s (\frac{π}{4} - x) c o s (\frac{π}{4} - y) - s i n (\frac{π}{4} - x) s i n (\frac{π}{4} - y) = s i n (x + y)$

23. (i) sin 75°= sin (45°+30°)

Using sin (x + y)= sin x cos y + cos x sin y we can write

9. sin x = 3/5, x lies in second quadrant.

9. Kindly go through the solution

27. sin (n + 1)xsin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x

27. L.H.S $L.HS = s i n (x + 1) x s i n (x + 2) x + c o s (x + 1) x c o s (x + 2) x .$

$= c o s (x + 1) x c o s (x + 2) x + s i n (x + 1) x s i n (x + 2) x .$

Let A = (n+1)x and B = (n+2)x

So, L.H.S = cosAcosB + sin Asin B

$= c o s (A - B)$

Putting values of A and B we get,

L.H.S = $L.H.S = c o s [(n + 1) x - (n + 2) x]$

$= c o s [n x + x - n x - 2 x]$

$= c o s (- x)$

$= c o s x = R.H.S$ R.H.S

54. (cos x + cos y)² + (sin x – sin y)= 4 cos² $\frac{x + y}{2}$

54. L.H.S. = (cos x + cos y)² + (sin x- sin y)²

Using,

cos A + cos B = 2 cos $\frac{A+B}{2}$ cos $\frac{A-B}{2}$

sin A - sin B = 2 cos $\frac{A+B}{2}$ sin $\frac{A - B}{2 .}$

L.H.S. = ${[2 \cdot c o s \frac{x + y}{2} c o s \frac{x - y}{2}]}^{2} + {[2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2}$ .

= 4. cos² $(\frac{x + y}{2})$ cos² $(\frac{x - y}{2})$ .. + 4 cos² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$ .

= 4 cos² $(\frac{x + y}{2})$ $[c o s^{2} (\frac{x - y}{2}) + s i n^{2} (\frac{x - y}{2})]$

= 4 cos² $(\frac{x + y}{2})$ [ $?$ cos²θ+ sin²qθ = 1].

= R.H.S.

56. sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x

56. L.H.S = sin x + sin 3x + sin 5x + sin 7x.

= (sin x + sin 7x) + (sin 3x + sin 5x)

Using,

sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

L.H.S. = 2. Sin $\frac{x + 7 x}{2}$ cos $\frac{x - 7 x}{2}$ + 2 sin $\frac{3 x + 5 x}{2}$ cos $\frac{3 x - 5 x}{2}$

= 2 sin $\frac{8 x}{2}$ cos $(- \frac{6 x}{2})$ + 2 sin $\frac{8 x}{2}$ cos $(- \frac{2 x}{2})$

= 2 sin 4x cos 3x + 2 sin 4x cosx.[ $?$ cos (-x) = cosx]

= 2 sin 4x[cos 3x + cosx]

Using cos A + cos B = 2 cos $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

So, L.H.S. = 2 sin 4x $[2 \cdot c o s \frac{3 x + x}{2} c o s \frac{3 x - x}{2}] .$

= 2 sin 4x $[2 \cdot c o s \frac{4 x}{2} \cdot c o s \frac{2 x}{2}]$

= 4 sin 4x. cos 2x cosx = R.H.S.

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Find the principal and general solutions of the following equations:

43. tan x = √3

43. tanx = √3

We have, tan x = √3

Since tan x is (+) ve the principal solution lies in I^st and III^nd quadrant

Now, tan x = √3 = tan $\frac{π}{3}$ . = tan $(π + \frac{π}{3})$

Principal solution are x = $\frac{π}{3}$ and $(π + \frac{π}{3})$

$\frac{π}{3}$ = and $(\frac{3 π + π}{3})$

$\frac{π}{3}$ = and $\frac{4 π}{3}$ .

As tan x = tan $\frac{π}{3}$

The general solution is.

x = np + $\frac{π}{3}$ , n∈z

55. (cos x – cos y)²+ (sin x – sin y)² = 4 sin² $\frac{x - y}{2}$

55. L.H.S = (cos x-cos y)² + (sin x- sin y)²

= ${[- 2 s i n \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2} + {[2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2}$

= 4 sin² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$ + 4 cos² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$

= 4 sin² $(\frac{x - y}{2})$ $[s i n^{2} (\frac{x + y}{2}) + c o s^{2} (\frac{x + y}{2})]$

= 4 $s i n^{2} (\frac{x - y}{2})$ . [ $?$ sin²∅ + cos²∅= 1]

= R.H.S.

Class 11 Math Trigonometric Functions Exercise 3.3 Solution

18. $s i n^{2} \frac{π}{6} + c o s^{2} \frac{π}{3} - t a n^{2} \frac{π}{4} = - \frac{1}{2}$

18.

$\begin{array}{l} {(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{2} - 1^{2} \\ = \frac{1}{4} + \frac{1}{4} - 1 \\ = \frac{1 + 1 + 4}{4} \\ = \frac{- 2}{4} \\ = \frac{- 1}{2} \end{array}$

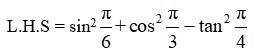
=R.H.S

10. cot x = 3/4, x lies in third quadrant.

10. Kindly go through the solution

11. sec x = 13/5, x lies in fourth quadrant.

11. Kindly go through the solution

3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

3. Given that a wheel makes 360 revolutions in one minute

Then, number of revolutions in one second = $\frac{360}{60}$ =6.

In 1 complete revolution the wheel turns 360°= 2π radian.

So, In 6 revolution, the wheel will turns 6×2π radian = 12π radian.

Hence, in one second the wheel will turn an angle of 12π radian.

Class 11 Chapter 3 Trigonometric Functions Exercise 3.2 Solution

Class 11 Math Exercise 3.2 focuses on the definition of trigonometric functions, understanding their domains and ranges, and solving problems based on their properties. The ex 3.2 class 11 Math covers key topics such as the definition of sine, cosine, tangent, and other trigonometric functions, and the fundamental concept of signs of trigonometric functions in different quadrants, helping students understand the variation of these functions across the coordinate plane. Class 11 Math Exercise 3.2 comprises 9 questions. Students can check the complete solution of the following exercise;

Class 11 Trigonometric Functions Exercise 3.2 Solution

Find the values of other five trigonometric functions in Exercises 1 to 5.

Q1. cos x = –1/2 , x lies in third quadrant.

Q.2. sin x = 3/5, x lies in second quadrant.

Q.3. cot x = 3/4, x lies in third quadrant.

Q4. sec x = 13/5, x lies in fourth quadrant.

Q5. tan x = –5/12, x lies in second quadrant.

Find the values of the trigonometric functions in Exercises 6 to 10.

Q6. sin 765°

A.6. sin 765°

We know that value of sun x repeats after an interval of 2π or 360°.

Sin (765°) = sin (2×360°+45°)

= sin 45°

= 1/√2.

Q7. cosec (-1410°)

A.7. cosec (- 1410°)

As value of cosec x repeats after interval of 2π or 360°

∴ cosec (-1410°) = cosec (4×360°-1410°)

=cosec (1440°-1410°)

= cosec 30°

= 2.

Q8. tan19π/3

= tan

(3 \times 2 π + \frac{π}{3})

= tan

\frac{π}{3}

= √3

Q9. $s i n (- \frac{11 π}{3})$

Q10. $c o t (- \frac{15 π}{4})$

Class 11 Chapter 3 Trigonometric Functions Exercise 3.3 Solution

Class 11 Math Ex 3.3 focuses on the fundamental trigonometric identities ( $\sin^2 x + \cos^2 x = 1$ , $1 + \tan^2 x = \sec^2 x$ , and $1 + \cot^{2} x = \csc^{2} x$ ) and properties of trigonometric functions. Trigonometric function Exercise 3.3 also deals with the simplification and transformation of trigonometric expressions using these identities. This Exercise 3.3 class 11 contains 25 questions and their detailed solutions. Students can check the complete solution of the exercise 3.3 below;

Class 11 Math Trigonometric Functions Exercise 3.3 Solution

Q1. $s i n^{2} \frac{π}{6} + c o s^{2} \frac{π}{3} - t a n^{2} \frac{π}{4} = - \frac{1}{2}$

A.1.

$\begin{array}{l} {(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{2} - 1^{2} \\ = \frac{1}{4} + \frac{1}{4} - 1 \\ = \frac{1 + 1 + 4}{4} \\ = \frac{- 2}{4} \\ = \frac{- 1}{2} \end{array}$

=R.H.S

Q2. $2 S i n^{2} \frac{π}{6} + c o s e c^{2} \frac{7 π}{6} c o s^{2} \frac{π}{3} = \frac{3}{2}$

$= \frac{1}{2} + 4 . \frac{1}{4}$

$= \frac{1}{2} + 1$ $= \frac{3}{2}$

= R.H.S.

Q3.

c o t^{2} \frac{π}{6} + c o s e c \frac{5 π}{6} + 3 t a n^{2} \frac{π}{6} = 6

Q4.

2 s i n^{2} \frac{3 π}{4} + 2 c o s^{2} \frac{π}{4} + 2 s e c^{2} \frac{π}{3} = 10

Q5. Find the value of:

(i) sin 75° (ii) tan 15°

A.5. (i) sin 75°= sin (45°+30°)

Using sin (x + y)= sin x cos y + cos x sin y we can write

sin 75°

= sin 45°cos 30°+ 45° sin 30°

Prove the following:

Q6. $c o s (\frac{π}{4} - x) c o s (\frac{π}{4} - y) - s i n (\frac{π}{4} - x) s i n (\frac{π}{4} - y) = s i n (x + y)$

Q7.

\frac{t a n (\frac{π}{4} + x)}{t a n (\frac{π}{4} - x)} = {(\frac{1 + t a n x}{1 - t a n x})}^{2}

Q8.

Q9. $c o s (\frac{3 π}{2} + x) c o s (2 π + x) [c o t (\frac{3 π}{2} - x) + c o t (2 π + x)] = 1$

A.9. L.H.S $L.H.S. = c o s (\frac{3 π}{2} + x) c o s (2 π + x) [c o t (\frac{3 π}{2} - x) + c o t (2 π + x)]$

Here,

$c o s (\frac{3 π}{2} + x) = c o s (\frac{4 π - π}{2} + x) = c o s (2 π - \frac{π}{2} + x)$

$= c o s [2 π - (\frac{π}{2} - x)]; VI quadrant.$

$c o s (\frac{π}{2} - x); i I^{st} quadrant.$

$= s i n x$

$c o s (2 x + x) = c o s x, as x lies in I^{st} quadrant.$

$c o t (2 π + x) = c o t x; as x lies in I^{st} quadrant.$

$c o t (\frac{3 π}{2} - x) = c o t [\frac{4 π - π}{2} - x]$

$= c o t [2 π - \frac{π}{2} - x]$

$= c o t [2 x - (\frac{π}{2} + x)]; V I^{th} quadrant.$

$= - c o t (\frac{π}{2} + x); I I^{nd} quadrat.$

$= - (- t a n x)$

$= t a n x .$

So.L.H.S $L.H.S = s i n x c o s x [t a n x + c o t x]$

$= s i n x c o s x [\frac{s i n x}{c o s x} + \frac{c o s x}{s i n x}]$

$= s i n x c o s x \frac{(s i n^{2} x + c o s^{2} x)}{c o s x s i n x}$

$= s i n^{2} x + c o s^{2} x$

= 1

= R.H.S.

Q10. sin (n + 1)xsin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x

A.10. L.H.S $L.HS = s i n (x + 1) x s i n (x + 2) x + c o s (x + 1) x c o s (x + 2) x .$

$= c o s (x + 1) x c o s (x + 2) x + s i n (x + 1) x s i n (x + 2) x .$

Let A = (n+1)x and B = (n+2)x

So, L.H.S = cosAcosB + sin Asin B

$= c o s (A - B)$

Putting values of A and B we get,

L.H.S = $L.H.S = c o s [(n + 1) x - (n + 2) x]$

$= c o s [n x + x - n x - 2 x]$

$= c o s (- x)$

$= c o s x = R.H.S$ R.H.S

Q11. $c o s (\frac{3 π}{4} + x) - c o s (\frac{3 π}{4} - x) = -\sqrt2 s i n x$

A.11. L.H.S = $L.H.S = c o s (\frac{3 π}{4} + x) - c o s (\frac{3 π}{4} - x)$

Using cos (A + B) = cos A cos B – sin A sin B

and cos (A – B) = cos A cos B + sin A sin B

$L.H.S = [c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x] - [c o s \frac{3 π}{4} c o s x + s i n \frac{3 π}{4} s i n x]$

$= c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x - c o s \frac{3 π}{4} c o s x - s i n \frac{3 π}{4} s i n x .$

$= - 2 s i n \frac{3 π}{4} s i n x .$

$= - 2 s i n (\frac{4 π - π}{4}) s i n x .$

Q12. sin²6x – sin²4x = sin 2x sin 10x

A.12. L.H.S $L.H.S = s i n^{2} 6 x - s i n^{2} 4 x .$

$= (s i n 6 x + s i n 4 x) (s i n 6 x - s i n 4 x) . [a^{2} - b^{2} = (a - b) (a + b)]$

So,

L.H.S = $L.H.S. = (2 s i n (\frac{6 x + 4 x}{2}) c o s (\frac{6 x - 4 x}{2})) (2 c o s (\frac{6 x + 4 x}{2}) s i n (\frac{6 x - 4 x}{2}))$

$= (2 s i n \frac{10 x}{2} c o s \frac{2 x}{2}) (2 c o s \frac{10 x}{2} s i n \frac{2 x}{2})$

$= 2 s i n 5 x c o s x \cdot 2 c o s 5 x s i n x$

$= 2 s i n 5 x c o s 5 x \cdot 2 c s i n x c o s x .$

As $s i n 2 θ = 2 s i n θ c o s θ$ we can write.

$L.H.S = s i n (2 \times 5 x) = s i n (2 \times x)$

$= s i n 10 x s i n 2 x = R.H.S.$ R.H.S

Q13. cos²2x – cos²6x = sin 4x sin 8x

A.13. L.H.S $L.H.S = c o s^{2} 2 x - c o s^{2} 6 x$

$= (c o s 2 x + c o s 6 x) (c o s 2 x - c o s 6 x) [∵ a^{2} - b^{2} = (a - b) (a + b)]$

L.H.S =

L.H.S = [2 c o s (\frac{2 x + 6 x}{2}) c o s (\frac{2 x - 6 x}{2})] [- 2 s i n \frac{2 x + 6 x}{2} s i n (\frac{2 x - 6 x}{2})]

= [2 c o s \frac{8 x}{2} c o s (- \frac{4 x}{2})] [- 2 s i n (\frac{8 x}{2}) s i n (- \frac{4 x}{2})]

= 2 c o s 4 x c o s 2 x \times 2 s i n 4 x \cdot s i n 2 x [∵ c o s (- x) = c o s x; s i n (- x) = - s i n x]

= 2 s i n 4 x c o s 4 x \times 2 s i n 2 x c o s 2 x

As sin 2θ = 2 sinθ cosθ.

L.H.S. = sin (2*4x) sin(2*2x)

= sin 8x sin 4x

= R.H.S.

Q14. sin2 x + 2 sin 4x + sin 6x = 4 cos²x sin 4x

A.14. L.H.S. = sin 2x + 2 sin 4x + sin 6x

Using sin A + sin B = 2 sin A + B/2 cos A - B/2 we have,

L.H.S. = (sin 2x + sin 6x) + 2 sin 4x

$= 2 s i n (\frac{2 x + 6 x}{2}) c o s (\frac{2 x - 6 x}{2}) + 2 s i n 4 x .$

$= 2 s i n \frac{8 x}{2} c o s (- \frac{4 x}{2}) + 2 s i n 4 x .$

$= 2 s i n 4 x c o s 2 x + 2 s i n 4 x [∵ c o s (- x) = x]$

$= 2 s i n 4 x [c o s 2 x + 1]$

We know that,

$c o s 2 x = 2 c o s^{2} x - 1$

$\Rightarrow c o s 2 x + 1 = 2 c o s^{2} x$

Hence,

L.H.S $= 2 s i n 4 x (2 c o s^{2} x)$

$= 4 c o s^{2} x s i n 4 x$

= R.H.S

Q15. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

A.15. L.H.S $= c o t 4 x (s i n 5 x + s i n 3 x)$

$= c o t 4 x [2 s i n \frac{8 x}{2} c o s \frac{2 x}{2}]$

$= \frac{c o s 4 x}{4 x} \times 2 s i n 4 x c o s x$

$= 2 \cdot c o s 4 x \cdot c o s x$

R.H.S $= c o t x [s i n 5 x - s i n 3 x]$

$= c o t x [2 c o s \frac{8 x}{2} \cdot s i n \frac{2 x}{2}]$

$= \frac{c o s x}{s i n x} \cdot 2 c o s 4 x s i n x$

$= 2 \cdot c o s 4 x \cdot c o s x .$

Hence, L.H.S. = R.H.S.

Q16. $\frac{c o s 9 x - c o s 5 x}{s i n 17 x - s i n 3 x} = - \frac{s i n 2 x}{c o s 10 x}$

A.16. $= \frac{c o s 9 x - c o s 5 x}{s i n 17 x - s i n 3 x}$

$= \frac{- 2 s i n (\frac{9 x + 5 x}{2}) s i n (\frac{9 x - 5 x}{2})}{2 c o s (\frac{17 x + 3 x}{2}) s i n (\frac{17 x - 3 x}{2})}$

$= \frac{- s i n \frac{14 x}{2} s i n \frac{4 x}{2}}{c o s \frac{20 x}{2} s i n \frac{14 x}{2}} = \frac{- s i n 7 x s i n 2 x}{c o s 10 x s i n 7 x} = \frac{- s i n 2 x}{c o s 10 x}$

= R.H.S

Q17. $\frac{s i n 5 x + s i n 3 x}{c o s 5 x + c o s 3 x} = t a n 4 x$

A.17. $= \frac{s i n 5 x + s i n 3 x}{c o s 5 x + c o s 3 x .}$

$= \frac{2 s i n (\frac{5 x + 3 x}{2}) c o s (\frac{5 x - 3 x}{2})}{2 c o s (\frac{5 x + 3 x}{2}) c o s (\frac{5 x - 3 x}{2})}$

$= \frac{s i n \frac{8 x}{2} c o s \frac{2 x}{2}}{c o s \frac{8 x}{2} c o s \frac{2 x}{2}}$

$= \frac{s i n 4 x}{c o s 4 x} = t a n 4 x =$ R.H.S

Q18. $\frac{s i n x - s i n y}{c o s x + c o s y} = t a n \frac{x - y}{2}$

A.18. L.H.S: = $L.H. S: = \frac{s i n x - s i n y}{c o s x + c o s y}$

$= \frac{2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}}{2 c o s \frac{x + y}{2} c o s \frac{x - y}{2}}$

$= \frac{s i n (\frac{x - y}{2})}{c o s (\frac{x - y}{2})}$

$= t a n (\frac{x - y}{2}) = R.H.S.$ = R.H.S.

Q19. $\frac{s i n x + s i n 3 x}{c o s x + c o s 3 x} = t a n 2 x$

A.19. $= \frac{s i n x + s i n 3 x}{c o s x + c o s 3 x}$

$= \frac{2 (\frac{x + 3 x}{2}) c o s (\frac{x - 3 x}{2})}{2 c o s (\frac{x + 3 x}{2}) c o s (\frac{x - 3 x}{2})}$

$= \frac{s i n \frac{4 x}{2}}{c o s \frac{4 x}{2}}$

$= \frac{s i n 2 x}{c o s 2 x}$

$= t a n 2 x =$ R.H.S

Q20. $\frac{s i n x - s i n 3 x}{s i n^{2} x - c o s^{2} x} = 2 s i n x$

A.20. $= \frac{s i n x - s i n 3 x}{s i n^{2} x - c o s^{2} x}$

$= \frac{2 c o s (\frac{x + 3 x}{2}) s i n \frac{x - 3 x}{2}}{- (c o s^{2} x - s i n^{2} x)}$

$= \frac{2 c o s \frac{4 x}{2} s i n (- \frac{2 x}{2})}{- c o s 2 x} [∵ c o s 2 x = c o s^{2} x - s i n^{2} x]$

$= - \frac{2 c o s 2 x s i n x}{- c o s 2 x} [∵ s i n (- x) = - s i n x]$

= 2 sin x

= R.H.S.

Q21. $\frac{c o s 4 x + c o s 3 x + c o s 2 x}{s i n 4 x + s i n 3 x + s i n 2 x} = c o t 3 x$

A.21. L.H.S $= \frac{c o s 4 x + c o s 3 x + c o s 2 x}{s i n 4 x + s i n 3 x + s i n 2 x .}$

$= \frac{(c o s 4 x + c o s 2 x) + c o s 3 x}{(s i n 4 x + s i n 2 x) + s i n 3 x} .$

$= \frac{2 c o s (\frac{4 x + 2 x}{2}) c o s (\frac{4 x - 2 x}{2}) + c o s 3 x}{2 s i n (\frac{4 x + 2 x}{2}) c o s (\frac{4 x - 2 x}{2}) s i n 3 x} .$

$= \frac{2 c o s \frac{6 x}{2} c o s \frac{2 x}{2} + c o s 3 x}{2 s i n \frac{6 x}{2} c o s \frac{2 x}{2} + s i n 3 x}$

$= \frac{2 c o s 3 x c o s x + c o s 3 x}{2 s i n 3 x c o s x + 3 x}$

$= \frac{c o s 3 x}{s i n 3 x} \times \frac{(2 c o s x + 1)}{(2 c o s x + 1)}$

$= c o t 3 x =R.H.S$

Q22. cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1

A.22. L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x.

= cot x cot 2x – cot 3x (cot 2x + cot x)

= cot x cot 2x – (cot 2x + cot x)[cot (2x + x)]

We know that,

$c o t (A +B) = \frac{c o tA c o tB - 1}{c o tA + c o tB}$ we can write

$L.H.S= c o t x c o t 2 x - (c o t 2 x + c o t x) [\frac{c o t 2 x \cdot c o t x - 1}{c o t 2 x + c o t x}]$

= cot x cot 2x – cot 2x cot x + 1

= 1

= R.H.S.

Q23.

t a n 4 x = \frac{4 t a n x (1 - t a n^{2} x)}{1 - 6 t a n^{2} x + t a n^{4} x}

A.23. L.H.S. = tan 4x

We know that,

$t a n 2 = \frac{2 t a n}{1 - t a n^{2}} .$ , we can write

$L.H.S= t a n 2 (2 x) = \frac{2 t a n 2 x}{1 - t a n^{2} 2 x .}$

$= \frac{2 (\frac{2 t a n x}{1 - t a n^{2} x})}{1 - {(\frac{2 t a n x}{1 - t a n^{2} x})}^{2}}$

$= \frac{\frac{4 t a n x}{(1 - t a n^{2} x)}}{\frac{{(1 - t a n^{2} x)}^{2} - 4 t a n^{2} x}{{(1 - t a n^{2} x)}^{2}}}$

$= \frac{4 t a n x \times (1 - t a n^{2} x)}{1 + t a n^{4} x - 2 t a n^{2} x - 4 t a n^{2} x}$

$= \frac{4 t a n x (1 - t a n^{2} x)}{1 - 6 t a n^{2} x + t a n^{4} x}$

= R.H.S.

Q24. cos 4x = 1 – 8sin²x cos²x

A.24. L.H.S. = cos 4x.

= cos 2(2x)

= 1 – 2 Sin²(2x) [ cos 2x = 1 – 2 Sin²x]

= 1 – 2 [2 sin xcosx]²[ sin 2x = 2 sin xcos x]

= 1 – 2 [4 sin²xcos²x]

= 1 – 8 sin²xcos²x

= R.H.S.

Q25. cos 6x = 32 cos⁶x – 48cos⁴x + 18 cos²x – 1

A.25. L.H.S. = cos 6x

= cos 3(2x)

= 4 cos³2x – 3 cos 2x [Q cos 3A = 4 cos³A – 3cos A]

= 4[(2 cos²x – 1)³] – 3[(2 cos²x – 1)] [Q cos 2x = 2 cos²x – 1]

= 4[(2 cos²x)³ + 3[(2 cos²x)²(–1) + 3(2 cos²x)(–1)² + (–1)³] – 3(2 cos²x) + 3

{Q (a + b)³= a³ + b³ + 3a²b + 3ab²}

= 4[8 cos⁶x – 12 cos⁴x + 6cos²x – 1] – 6 cos²x + 3.

= 32 cos⁶x – 48 cos⁴x + 24 cos²x – 4 – 6cos²x + 3

= 32 cos⁶x – 48 cos⁴x + 18 cos²x – 1

= R.H.S.

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Class 11 Math Ex 3.4 focuses on the general solutions of trigonometric equations. Ex 3.4 class 11 Math focuses on solving basic trigonometric equations involving sine, cosine, tangent, and other trigonometric functions. This exercise is crucial in developing a deeper understanding of how trigonometric functions behave and how their equations can be solved systematically.

It covers the general solution of trigonometric equation

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Find the principal and general solutions of the following equations:

Q1. tan x = √3

A.1. tanx = √3

We have, tan x = √3

Since tan x is (+) ve the principal solution lies in I^st and III^nd quadrant

Now, tan x = √3 = tan $\frac{π}{3}$ . = tan $(π + \frac{π}{3})$

Principal solution are x = $\frac{π}{3}$ and $(π + \frac{π}{3})$

$\frac{π}{3}$ = and $(\frac{3 π + π}{3})$

$\frac{π}{3}$ = and $\frac{4 π}{3}$ .

As tan x = tan $\frac{π}{3}$

The general solution is.

x = np + $\frac{π}{3}$ , n∈z

Q2. Secx = 2

A.2. Secx = 2. .

We have, Secx = 2, | Secx is (+)ve the principal solution lies in I^st and IV^thquadrent.

= $\frac{π}{3}$ and $\frac{6 π - π}{3}$

= $\frac{π}{3}$ and $\frac{5π}{3}$ .

As secx = sec $\frac{π}{3}$ . cosx = cos $\frac{π}{3}$ $[∴ s e c x = \frac{1}{c o s x}]$

The general solution is

x = 2nπ ± $\frac{π}{3}$ , n ∈ z.

Q3. cot x = -√3

A.3. We have, cot x = -√3 i.e., cot x is negative

So, the principal solution lies in II^nd and IV^th quadrant.

So the principal solution are a = $(π - \frac{π}{6})$ and $(2 π - \frac{π}{6})$

= $(\frac{6 π - π}{6})$ and $(\frac{12 π - π}{6})$

= $\frac{5 π}{6}$ and $\frac{11 π}{6} .$

As cot x = cot $\frac{5 π}{6}$ tan x = tan $\frac{5 π}{6}$ $[∵ c o t x = \frac{1}{t a n x}]$

The general solution has the form.

x = n+ $\frac{5 π}{6}$ , nz

Q4. cosec x = – 2

A.4.We have cosec x = 2 .i e, cosec x = (-)ve,

So, the principal solution lies in IIInd and IVth quadrent.

Now, cosec x = -2 = -cosec $\frac{π}{6}$ = cosec $(π + \frac{π}{6}$ = cosec $(2 π - \frac{π}{6})$

So the principal solution are x = $(π + \frac{π}{6})$ and $(2 π - \frac{π}{6})$

= $(\frac{6 π + π}{6})$ and $(\frac{12 π - π}{6})$

= $\frac{7 π}{6}$ and $\frac{11 π}{6} .$

As cosec x = cosec $\frac{7 π}{6}$ ⇒sin x = sin $\frac{7 π}{c}$ $[∵ c o s e c x = \frac{1}{s i n x}]$

The general solution has the form,

x = nπ + (-1)n $\frac{7 π}{6}$ , n∈z.

Find the general solution for each of the following equations:

Q5. cos 4 x = cos 2 x

A.5. We have,

cos 4x = cos 2x.

⇒ cos 4x-cos 2x = 0.

⇒ -2 sin $(\frac{4 x + 2 x}{2})$ sin $(\frac{4 x - 2 x}{2})$ = 0.

⇒sin $\frac{6 x}{2}$ sin $\frac{2 x}{2}$ = 0

⇒sin 3x sin x = 0.

∴sin 3x = 0 or sin x = 0

3x = nπ or x = nπ, n∈z,

⇒x = $\frac{n π}{3}$ or x = nπ, n∈z

Q6. cos 3x + cos x – cos 2x = 0

A.6. We have,

cos 3x + cosx-cos 2x = 0.

(cos 3x + cosx) cos 2x = 0

Using cos A + cos B = 2 cos $\frac{A+B}{2}$ cos $\frac{A-B}{2}$

2 cos $(\frac{3 x + x}{2})$ cos $(\frac{3 x - x}{2})$ - cos 2x = 0.

2 cos $\frac{4 x}{2}$ cos $\frac{2 x}{2}$ - cos 2x = 0

2 cos 2xcosx - cos 2x = 0

cos 2x. (2 cosx - 1) = 0.

cos 2x = 0 or 2 cosx -1 = 0.

2x = (2n + 1) $\frac{π}{2}$ , n∈z or cosx = $\frac{1}{2}$ = cos $\frac{π}{3}$

x = (2n + 1) $\frac{π}{4}$ , n∈z or x = 2nx± $\frac{π}{3}$ , n∈z.

Q7. sin 2x + cos x = 0

A.7. We have,

sin 2x + cosx = 0.

2 sin cosx + cosx = 0( $∵$ sin 2x = 2 sin xcosx)

cosx (2 sin x + 1) = 0.

cosx = 0 or 2 sinx + 1 = 0.

x = (2n + 1) $\frac{π}{2}$ , n∈z or sin x = $\frac{1}{2}$ = -sin $\frac{π}{6}$ = sin π + $\frac{π}{6}$ = sin $\frac{7 π}{6} .$

x = (2n + 1) $\frac{π}{2}$ , x∈z or x= nπ + (-1)ⁿ $\frac{7 π}{6},$ n∈z.

Q8. sec²2x = 1– tan 2x

A.8. We have,

sec² 2x = 1 tan 2x

1 + tan² 2x = 1 tan 2x[ sec²x = 1 + tan²x]

tan² 2x + tan 2x = 0.

tan 2x (tan 2x + 1) = 0.

tan 2x = 0 or tan 2x + 1 = 0.

2x = nπ, x∈z or tan 2x = -1 = -tan $\frac{π}{4}$ = tan π- $\frac{π}{4}$ = tan $\frac{3 π}{4} .$

x= $\frac{n π}{2}$ , n∈z or 2x = nπ + $\frac{3 π}{4}$ , n∈z.

x = $\frac{n π}{2} + \frac{3 π}{8},$ n∈z

Q9. sin x + sin 3x + sin 5x = 0

A.9. We have,

sinx + sin 3x + sin 5x = 0.

(sinx + sin 5x) + sin 3x = 0.

Using sin A + sin B = 2 sin $\frac{A+B}{2}$ cos $\frac{A-B}{2}$ .

2 sin $(\frac{x + 5 x}{2})$ cos $(\frac{x - 5 x}{2})$ + sin 3x = 0.

2 sin $\frac{6 x}{2}$ cos $\frac{-4 x}{2}$ + sin 3x = 0.

2 sin 3xcos (-2x) + sin 3x = 0.

sin 3x [2 cos 2x + 1] = 0[ $∵$ cos (-x) = cosx].

sin 3x = 0 or 2 cos 2x + 1 = 0.

3x = nπ, n∈z. or cos 2x = $\frac{-1}{2}$ = -cos $\frac{π}{3}$ = cos π - $\frac{π}{3}$ = cos $\frac{2 π}{3}$

x= $\frac{n π}{3}$ , n∈z or 2x = 2nπ± $\frac{2 π}{3}$ .

x = nπ± $\frac{π}{3}$ , n∈z.

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Trigonometric Functions Miscellaneous Exercise covers all the topics learned throughout the chapter such as angle measurement in degrees and radians, unit circle-based trigonometric functions, fundamental identities, and trigonometric equations. It also reinforces concepts such as domain and range of trigonometric functions, periodicity, symmetry, and sign variations across different quadrants. Students can check the complete solution of the Miscellaneous exercise below;

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Q1. $2 c o s \frac{π}{13} c o s \frac{9 π}{13} + c o s \frac{3 π}{13} + c o s \frac{5 π}{13} = 0$

A.1. L.H.S. = 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + cos $\frac{3 π}{13}$ + cos $\frac{5 π}{13}$ =∂ .

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2 cos $\begin{array}{l} (\frac{3 π}{13} + \frac{5 π}{13}) \\ \bar{2} \end{array}$ cos $\frac{(\frac{3 π}{13} - \frac{5 π}{13})}{2}$

$[∵ c o s A + c o s B = 2 c o s \frac{A + B}{2} c o s \frac{A - B}{2}]$

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2. cos $(\frac{8 π / 13}{2})$ cos $(\frac{- 2 π / 13}{2})$

= 2 cos $\frac{π}{13}$ cos $\frac{9 π}{13}$ + 2 cos $\frac{4 π}{13}$ cos $\frac{π}{13}$ [ $∵$ cos (x) = cosx].

= 2 cos $\frac{π}{13}$ $[c o s \frac{9 π}{13} + c o s \frac{4 π}{13}] .$

= 2 cos $\frac{π}{13} [2 \cdot c o s (\frac{\frac{9 π}{13} + \frac{4 π}{13}}{2}) c o s (\frac{\frac{9 π}{13} - \frac{4 π}{13}}{2})]$

= 2 cos $\frac{π}{13}$ $[2 \cdot c o s (\frac{13 π / 13}{2}) c o s (\frac{5 π / 13}{2})]$

= 2 cos $\frac{π}{3}$ × 2 ×cos $\frac{π}{2}$ × cos $\frac{5 π}{26}$ .

= 2 cos $\frac{π}{2}$ 2× 0×cos $\frac{5 π}{26}$

= 0

= R.H.S.

Q2. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0

A.2. L.H.S = (sin 3x + sin x) + sin x + (cos 3x - cosx) cosx.

Using

Sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A-B}{2}$

cos A - cos B = -2 sin $\frac{A+B}{2}$ sin $\frac{A-B}{2}$ .

L.H.S. = $(2 s i n \frac{3 x + x}{2} c o s \frac{3 x - x}{2})$ sin x + $(- 2 s i n \frac{3 x + x}{2} s i n \frac{3 x - x}{2})$ cosx

= 2 sin $\frac{4 x}{2}$ cos $\frac{2 x}{2}$ sin x -2 sin $\frac{4 x}{2}$ sin $\frac{2 x}{2}$ cosx.

= 2 sin 2xcosx sin x -2 sin 2x sin xcosx

= 0 = R.H.S.

Q3. (cos x + cos y)² + (sin x – sin y)= 4 cos² $\frac{x + y}{2}$

A.3. L.H.S. = (cos x + cos y)² + (sin x- sin y)²

Using,

cos A + cos B = 2 cos $\frac{A+B}{2}$ cos $\frac{A-B}{2}$

sin A - sin B = 2 cos $\frac{A+B}{2}$ sin $\frac{A - B}{2 .}$

L.H.S. = ${[2 \cdot c o s \frac{x + y}{2} c o s \frac{x - y}{2}]}^{2} + {[2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2}$ .

= 4. cos² $(\frac{x + y}{2})$ cos² $(\frac{x - y}{2})$ .. + 4 cos² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$ .

= 4 cos² $(\frac{x + y}{2})$ $[c o s^{2} (\frac{x - y}{2}) + s i n^{2} (\frac{x - y}{2})]$

= 4 cos² $(\frac{x + y}{2})$ [ $∵$ cos²θ+ sin²qθ = 1].

= R.H.S.

Q4. (cos x – cos y)²+ (sin x – sin y)² = 4 sin² $\frac{x - y}{2}$

A.4. L.H.S = (cos x-cos y)² + (sin x- sin y)²

= ${[- 2 s i n \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2} + {[2 c o s \frac{x + y}{2} s i n \frac{x - y}{2}]}^{2}$

= 4 sin² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$ + 4 cos² $(\frac{x + y}{2})$ sin² $(\frac{x - y}{2})$

= 4 sin² $(\frac{x - y}{2})$ $[s i n^{2} (\frac{x + y}{2}) + c o s^{2} (\frac{x + y}{2})]$

= 4 $s i n^{2} (\frac{x - y}{2})$ ..[ $∵$ sin²∅ + cos²∅= 1]

= R.H.S.

Q5. sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x

A.5. L.H.S = sin x + sin 3x + sin 5x + sin 7x.

= (sin x + sin 7x) + (sin 3x + sin 5x)

Using,

sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

L.H.S. = 2. Sin $\frac{x + 7 x}{2}$ cos $\frac{x - 7 x}{2}$ + 2 sin $\frac{3 x + 5 x}{2}$ cos $\frac{3 x - 5 x}{2}$

= 2 sin $\frac{8 x}{2}$ cos $(- \frac{6 x}{2})$ + 2 sin $\frac{8 x}{2}$ cos $(- \frac{2 x}{2})$

= 2 sin 4x cos 3x + 2 sin 4x cosx.[ $∵$ cos (-x) = cosx]

= 2 sin 4x[cos 3x + cosx]

Using cos A + cos B = 2 cos $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

So, L.H.S. = 2 sin 4x $[2 \cdot c o s \frac{3 x + x}{2} c o s \frac{3 x - x}{2}] .$

= 2 sin 4x $[2 \cdot c o s \frac{4 x}{2} \cdot c o s \frac{2 x}{2}]$

= 4 sin 4x. cos 2x cosx = R.H.S.

Q6. $\frac{(s i n 7 x + s i n 5 x) + (s i n 9 x + s i n 3 x)}{(c o s 7 x + c o s 5 x) + (c o s 9 x + c o s 3 x)} = t a n 6 x$

A.6. L.H.S. = $\frac{(s i n 7 x + s i n 5 x) + (s i n 9 x + s i n 3 x)}{(c o s 7 x + c o s 5 x) + (c o s 9 x + c o s 3 x)} .$

Using sin A + sin B = 2 sin $\frac{A + B}{2}$ cos $\frac{A - B}{2}$

cos A + cos B = 2 cos $\frac{A + B}{2}$ cos $\frac{A - B}{2} .$

Q7. sin 3x + sin 2x – sin x = 4sin x $c o s \frac{x}{2} c o s \frac{3 x}{2}$

A.7. L.H.S = sin 3x + sin 2x - sin x

= sin 3x - sin x + sin 2x.

= 2 cos $\frac{3 x + x}{2}$ .. sin $\frac{3 x - x}{2}$ + sin 2x $[∵ s i n A - s i n B = 2 c o s \frac{A + B}{2} s i n \frac{A - B}{2}]$

= 2 cos $\frac{4 x}{2}$ sin $\frac{2 x}{2}$ + sin 2x.

= 2 cos 2x sin x + 2 sin xcosx [ $∵$ sin 2x = 2sin xcosx]

= 2 sin x [cos 2x + cosx]

= 2 sin x $[2 c o s \frac{2 x + x}{2} c o s \frac{2 x - x}{2}]$ $[∵ c o s A + c o s B = 2 c o s \frac{A + B}{2} c o s \frac{A - B}{2}]$

= 2 sin x $[2 . c o s \frac{3 x}{2} c o s \frac{x}{2}]$

= 4 sin xcos $\frac{x}{2}$ . cos $\frac{3 x}{2}$ = R.H.S.

Find sin $\frac{x}{2}$ , cos $\frac{x}{2}$ and tan $\frac{x}{2}$ in each of the following :

Q8. tan x = − $\frac{4}{3}$ , x in quadrant II

A.8. We have, tan x= $\frac{- 4}{3}$ , x in IInd quadrant.

Since, $\frac{π}{2} < x < π$

$\frac{π}{4} < \frac{x}{2} < \frac{π}{2}$

sin $\frac{x}{2}$ , cos $\frac{x}{2}$ , tan $\frac{x}{2}$ are all positive.

Now, sec²x = 1 + tan²x = 1 + ${(\frac{- 4}{3})}^{2}$ = 1 + $\frac{16}{9}$ = $\frac{9 + 16}{9}$ = $\frac{25}{9}$

secx = ± $\frac{5}{3}$

cosx = ± $\frac{3}{5}$ .

cosx = $\frac{- 3}{5}$ as x is in IInd quadrant.

Now, 2 sin².. = 1 cosx. [cos 2x = 1 2 sin²x.]

2 sin² $\frac{x}{2}$ = 1 $(\frac{- 3}{5})$

2 sin² $\frac{x}{2}$ = 1 + $\frac{3}{5}$ = $\frac{5 + 3}{5}$ = $\frac{8}{5}$ .

sin² $\frac{x}{2}$ = $\frac{8}{2 \times 5}$ = $\frac{4}{5 .}$

Q9.cos x = −1/3, x in quadrant III

Q10. sin x = 1/4 in quadrant II

Explore exams which ask questions on Maths Ncert Solutions class 11th

Select your preferred stream

Engineering

Boards

View more exams

Maths Ncert Solutions class 11th Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Popular Courses After 12th

ScienceCommerceArts

Bachelor of Technology (BE/BTech)
Exams accepted
JEE Main | BITSAT | WBJEE
Bachelor of Architecture (BArch)
Exams accepted
NATA | AAT | ITM NEST
Bachelor of Science (BSc)
Exams accepted
CUET | UPCATET | IIT JAM
Bachelor of Computer Applications (BCA)
Exams accepted
BUMAT | GSAT | SET
Bachelor of Medicine & Bachelor of Surgery (MBBS)
Exams accepted
NEET | AYUSH | FMGE

View all courses after 12th

Chartered Accountancy (CA)
Exams accepted
CA Foundation
Company Secretary (CS)
Exams accepted
ICSI Exam
BCom in Accounting & Commerce
Exams accepted
BHU UET | GLAET | GD Goenka Test
Bachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBE
BBA/BMS
Exams accepted
IPMAT | NMIMS - NPAT | SET

View all courses after 12th

BA in Humanities & Social Sciences
Exams accepted
SUAT | JNUEE | BHU UET
Bachelor of Fine Arts (BFA)
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test

View all courses after 12th

News & Updates

Latest NewsPopular News

NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions

Trigonometry Class 11 NCERT Solutions Key Concepts

Class 11 Chapter 3 Trigonometric Functions: Key Topics, Weightage

Trigonometry Class 11 Weightage in JEE Main Exam

Try these practice questions

Important Formulas of Trigonometry Class 11

Trigonometric Functions Important Formulae for CBSE and Competitive Exams

More Useful Links

Class 11 Chapter 3 Trigonometric Functions NCERT Solution PDF: Free PDF Download

Class 11 Chapter 3 Trigonometric Functions Exercise-wise Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.1 Solution

Class 11 Chapter 3 Trigonometric Functions Ex 3.1 NCERT Solution

Commonly asked questions

Class 11 Trigonometric Functions Exercise 3.2 Solution

Class 11 Chapter 3 Trigonometric Functions Ex 3.1 NCERT Solution

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Class 11 Math Trigonometric Functions Exercise 3.3 Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.2 Solution

Class 11 Trigonometric Functions Exercise 3.2 Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.3 Solution

Class 11 Math Trigonometric Functions Exercise 3.3 Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Class 11 Chapter 3 Trigonometric Functions Exercise 3.4 Solution

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Class 11 Chapter 3 Trigonometric Functions Miscellaneous Exercise Solution

Explore exams which ask questions on Maths Ncert Solutions class 11th

Student Forum

Other Similar chapters for you

Popular Courses After 12th

News & Updates

LPU NEST Application Form 2026 (SOON) Live Updates; Official Website, Registration Link, Slot Booking

Board Exam Date Sheet 2026 Class 10th, 12th Live Updates; ICSE, Maharashtra, Tamil Nadu, GSEB Time Table Soon

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement