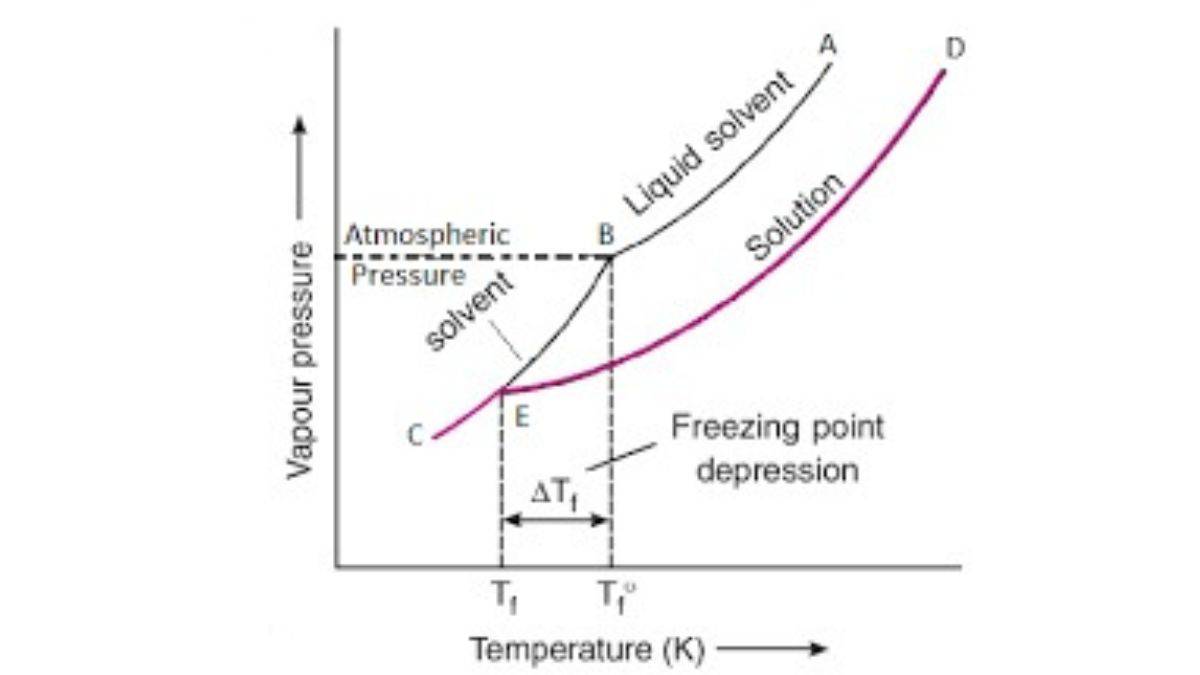
Depression in Freezing Point: Definition, Formulas, Applications & Notes

Q: Q: A 5% solution (by mass) of cane sugar in water has freezing point of 271K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.

A: 5% solution means 5g of cane sugar is present in 100g of solution Freezing point of solution = 271k Freezing point of pure water = 273.15k Molar mass of cane sugar(C12H22O11) = 12 × 12 + 1 × 22 + 16 × 11 = 342g Moles of cane sugar = mass/molar mass = 5/342 ⇒ n = 0.0146mol Molality of solution = moles of solute/mass of solvent(in kg) ⇒ M = 0.0146/0.095 ⇒ Molality = 0.154M Depression in freezing point = ΔTf = 273.15-271 = 2.15k Applying the formula: ΔTf = Kf × M Where ΔTf = depression in freezing point Kf = molal depression constant M = molality of solution ⇒ Kf = 2.15/0.154 ⇒ Kf = 13.96k kg mol-1 Second condition: mass of glucose = 5g Molar mass of glucose(C6H12O6) = 12 × 6 + 1 × 12 + 16 × 6 = 180g Moles of glucose = mass/molar mass ⇒ n = 5/180moles ⇒ n = 0.0278mol Molality of solution = moles of solute/mass of solvent(in kg) ⇒ molality = 0.0278/0.095 ⇒ M = 0.2926M Applying the formula: ΔTf = Kf × M Where ΔTf = depression in freezing point Kf = molal depression constant M = molality of solution ⇒ ΔTf = 13.96 × 0.2926 ⇒ ΔTf = 4.08k Freezing point of solution = 273.15 + 4.08 = 277.234k

Q: Q: Two elements A and B form compounds having formula AB2 and AB4 . When dissolved in 20 g of benzene (C6H6 ), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol^–1. Calculate atomic masses of A and B

A: let the molar masses of AB2 and AB4 be x and y respectively. Molar mass of benzene(C6H6) = 12 × 6 + 1 × 6 = 78 g/mol Moles of benzene = mass/molar mass = 20/78 n = 0.256mol ⇒ ΔTf = 2.3 K Kf = 5.1K kg mol-1 For AB2 Applying the formula: ΔTf = Kf × M Where ΔTf = depression in freezing point Kf = molal depression constant M = molality of solution ⇒ 2.3 = 5.1 × M1 ⇒ M1 = 0.451mol/kg For AB4 Applying the formula: ΔTf = Kf × M ΔTf = depression in freezing point Kf = molal depression constant M = molality of solution ⇒ 1.3 = 5.1 × M2 ⇒ M2 = 0.255mol/kg M1 = moles of solute/mass of solvent(in kg) M1 = 1/x / 0.02 = 1 / 0.02x = 0.451 ⇒ X = 110.86g M2 = moles of solute/mass of solvent(in kg) M2 = 1/y / 0.02 = 1 / 0.02y = 0.255 ⇒ y = 196.1g atomic mass of A be a and that of B be b g respectively. So, AB2 : a + 2b = 110.86 AB4: a + 4b = 196.1 ⇒ a = 25.59g ⇒ b = 42.64g

Q: Q: The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.

A: The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the pattern, Acetic acid< trichloroacetic acid< trifluoroacetic acid. This is because fluorine is more electronegative than chlorine. So, trifluoracetic acid is a stronger acid in comparison to trichloroacetic acid and acetic acid. And also, acetic acid is the weakest of all. Explanation: Stronger acid produces more number of ions, therefore it has more ΔTf(depression in freezing point), hence lower freezing point. As the acidic strength increases, the acid gets more and more ionised. Trifluoracetic acid ionizes to the largest extent. Hence, in this case, trifluoracetic acid being the strongest acid produces more number of ions(extent of ionisation and concentration of ions are more), high ΔTf(depression in freezing point)and lower freezing point and vice versa.

Q: Q: Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10^–3 , Kf = 1.86 K kg mol^–1 .

A: Mass of CH3CH2CHClCOOH = 10 g Mass of water = 250g Ka = 1.4 × 10–3, Kf = 1.86 K kg mol–1 Molar mass of CH3CH2CHClCOOH = 12 + 3 + 12 + 2 + 12 + 1 + 35.5 + 2 + 16 + 16 + 1 = 122.5 g mol–1 Number of moles of solute = Mass of Solute / Molar Mass → No. of moles = 10g / 122.5 g/mol ∴ No. of moles = 8.6 X 10–2 mol Now, Molality is given as, M = Number of moles of solute / kg of solvent M= 8.6 X 10–2 X 1000 g/mol / 250 g M = 0.3264 kg/mol CH3CH2CHClCOOH = CH3CH2CHClCOO- + H + Initial moles 1 0 0 Equilibrium moles (1-α) α α Total moles at equilibrium = (1-α) + 2 α = 1 + α In order to find out the depression in freezing point, values of i(vant Hoff’s factor) and α(degree of dissociation) are to be found out. To find out degree of dissociation, α ∴ i = 1.0654 Now, to find out the depression in freezing point,

Q: Q: 19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.00 C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.

A: Given- w1 = 500g W2 = 19.5g Kf = 1.86 K kg mol-1 Molar mass of CH2FCOOH = 12 + 2 + 19 + 12 + 16 + 16 + 1 = 78 g mol-1 The depression in freezing point is calculated by, → (where, m is the molality) = 1.86 X 19.5 / 78 X 1000/500 = 1.86 X 19.5 / 78 X 2 =0.93 ∴ Δtf (calculated) = 0.93 To find out the vant Hoff’s factor, we use the formula, i = observed Δtf / calculated Δtf i = 1.0 (given) / 0.93 ∴ i= 1.07 CH2FCOOH → CH2FCOO- + H + To find out the degree of dissociation α, we use Thus, the vant Hoff’s factor is 1.07 an the dissociation constant is 2.634x10-3

Updated on Sep 12, 2025 17:38 IST

By Vikash Kumar Vishwakarma

Depression in freezing point is a property of solutions observed when a non-volatile solid is added to the solvent, its vapour pressure decreases. This phenomenon is explained by Raoult's law. Freezing point depression has various applications such as de-icing roads, making Ice cream, food preservation, determining molar mass, etc.

Depression of freezing point is a topic in Class 12 Chemistry Chapter 1 Solutions. Students can learn about this topic through their textbook. Also, the experts at Shiksha have prepared an NCERT solution to help students prepare for the exam. CBSE Class 12 Chemistry Chapter 1 NCERT Solution is the best study material for self-assessment and preparation.

In this article, we will discuss what is depression in freezing point, depression of freezing point formulas, and the application of freezing point depression.

Also Check: NCERT Notes

Table of content

Defination of Depression in Freezing Point
Depression in Freezing Point Formula
Factors Affecting Depression in Freezing Point
Freezing Point and Depression of Freezing Point for Solvents
Uses of Freezing Point Depression
FAQs on Depression in Freezing Point

Defination of Depression in Freezing Point

The depression in freezing point is a colligative property of a solution. It is also known as freezing point depression. Depression is referred to as an event where the freezing point of a solution is lower than that of the pure solvent. The reason for this difference is that the presence of solute particles disrupts the regular crystal lattice structure that forms when a pure solvent freezes. The formula representation of the depression of freezing point is

ΔT_f = i×K_f×m

Depression in Freezing Point Formula

When a non-volatile solute is dissolved in the solvent, then the freezing point of the solution is lower than that of the pure solvent. This happens because a non-volatile solute decreases the vapour pressure of the liquid solution. A decrease in pressure lowers the freezing point. This lowering is called depression in freezing point.

$∆ T_{f} = K_{f} \cdot m$

Where:

ΔTf is the change in freezing point (in degrees Celsius or Kelvin).
Kf is the cryoscopic constant, which is a characteristic constant for a particular solvent.
m is the molality of the solute, which is the moles of solute per kilogram of solvent.

Important Topic:

CBSE Class 12 NCERT Notes	NCERT Class 12 Chemistry Notes
NCERT Class 12 Maths Notes for CBSE	Class 12 Physics NCERT Notes

Factors Affecting Depression in Freezing Point

The following factors affect freezing point depression.

Amount of solute
Solute and Solvent nature
Cryoscopic constant (Kf) of the solvent

Freezing Point and Depression of Freezing Point for Solvents

Check the table to know the freezing point and the depression freezing point for various solvents.

Solvent	Freezing Point (f. p / K)	Freezing Point Depression
Water	273.0	1.86
Benzene	278.6	5.12
Chloroform	209.6	4.79
Acetic acid	290.0	3.90
Ethanol	155.7	1.99
Diethyl ether	156.9	1.79

Also Check:

NCERT Class 11 Notes	Class 11 Physics Notes
Class 11 Chemistry NCERT Notes	Maths Class 11 NCERT Notes

Uses of Freezing Point Depression

The following are some important uses of freezing point depression.

Using the freezing point depression formula, the molar mass of a given solute can be calculated
The degree to which a solute dissociates in a solvent can also be calculated using the freezing point depression formula
In very cold areas where the temperatures range from 0^oC to -15^oC, NaCl is spread over the roads in order to lower the freezing point of water and thus prevent the formation of ice.
Radiator fluids which are used in many automobiles are usually made up of ethylene glycol and water. This prevents the freezing of the radiator during extreme cold seasons.

The freezing point of a solution is lower than that of the pure solvent due to the presence of solute particles, and the extent of this depression is determined by the molality of the solute and the cryoscopic constant of the solvent. This property is widely used in various fields, including chemistry and food science, to determine the concentration of solutes in solutions.

FAQs on Depression in Freezing Point

Q: A 5% solution (by mass) of cane sugar in water has freezing point of 271K. Calculate the freezing point of 5% glucose in water if freezing point of pure water is 273.15 K.

5% solution means 5g of cane sugar is present in 100g of solution

Freezing point of solution = 271k

Freezing point of pure water = 273.15k

Molar mass of cane sugar(C₁₂H₂₂O₁₁) = 12 × 12 + 1 × 22 + 16 × 11 = 342g

Moles of cane sugar = mass/molar mass = 5/342

⇒ n = 0.0146mol

Molality of solution = moles of solute/mass of solvent(in kg)

⇒ M = 0.0146/0.095

⇒ Molality = 0.154M

Depression in freezing point = ΔT_f = 273.15-271 = 2.15k

Applying the formula: ΔT_f = K_f × M

Where

ΔT_f = depression in freezing point

K_f = molal depression constant

M = molality of solution

⇒ K_f = 2.15/0.154

⇒ K_f = 13.96k kg mol^-1

Second condition: mass of glucose = 5g

Molar mass of glucose(C₆H₁₂O₆) = 12 × 6 + 1 × 12 + 16 × 6 = 180g

Moles of glucose = mass/molar mass

⇒ n = 5/180moles

⇒ n = 0.0278mol

Molality of solution = moles of solute/mass of solvent(in kg)

⇒ molality = 0.0278/0.095

⇒ M = 0.2926M

Applying the formula: ΔT_f = K_f × M

Where

ΔT_f = depression in freezing point

K_f = molal depression constant

M = molality of solution

⇒ ΔT_f = 13.96 × 0.2926

⇒ ΔT_f = 4.08k

Freezing point of solution = 273.15 + 4.08 = 277.234k

Q: Two elements A and B form compounds having formula AB2 and AB4 . When dissolved in 20 g of benzene (C6H6 ), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol^–1. Calculate atomic masses of A and B

A: let the molar masses of AB₂ and AB₄ be x and y respectively.

Molar mass of benzene(C₆H₆) = 12 × 6 + 1 × 6 = 78 g/mol

Moles of benzene = mass/molar mass = 20/78

n = 0.256mol

⇒ ΔT_f = 2.3 K

K_f = 5.1K kg mol^-1

For AB₂

Applying the formula: ΔT_f = K_f × M

Where

ΔT_f = depression in freezing point

K_f = molal depression constant

M = molality of solution

⇒ 2.3 = 5.1 × M₁

⇒ M₁ = 0.451mol/kg

For AB₄

Applying the formula: ΔT_f = K_f × M

ΔT_f = depression in freezing point

K_f = molal depression constant

M = molality of solution

⇒ 1.3 = 5.1 × M₂

⇒ M₂ = 0.255mol/kg

M₁ = moles of solute/mass of solvent(in kg)

M₁ = 1/x / 0.02 = 1 / 0.02x = 0.451

⇒ X = 110.86g

M₂ = moles of solute/mass of solvent(in kg)

M₂ = 1/y / 0.02 = 1 / 0.02y = 0.255

⇒ y = 196.1g

atomic mass of A be a and that of B be b g respectively.

So, AB₂ : a + 2b = 110.86

AB₄_: a + 4b = 196.1

⇒ a = 25.59g

⇒ b = 42.64g

Q: The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.

The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the pattern,

Acetic acid< trichloroacetic acid< trifluoroacetic acid.

This is because fluorine is more electronegative than chlorine. So, trifluoracetic acid is a stronger acid in comparison to trichloroacetic acid and acetic acid. And also, acetic acid is the weakest of all.

Explanation: Stronger acid produces more number of ions, therefore it has more ΔT_f(depression in freezing point), hence lower freezing point. As the acidic strength increases, the acid gets more and more ionised.

Trifluoracetic acid ionizes to the largest extent. Hence, in this case, trifluoracetic acid being the strongest acid produces more number of ions(extent of ionisation and concentration of ions are more), high ΔT_f(depression in freezing point)and lower freezing point and vice versa.

Q: Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10^–3 , Kf = 1.86 K kg mol^–1 .

Mass of CH₃CH₂CHClCOOH = 10 g

Mass of water = 250g

K_a = 1.4 × 10^–3,

K_f = 1.86 K kg mol^–1

Molar mass of CH₃CH₂CHClCOOH = 12 + 3 + 12 + 2 + 12 + 1 + 35.5 + 2 + 16 + 16 + 1

= 122.5 g mol^–1

Number of moles of solute = Mass of Solute / Molar Mass

→ No. of moles = 10g / 122.5 g/mol

∴ No. of moles = 8.6 X 10^–2 mol

Now, Molality is given as,

M = Number of moles of solute / kg of solvent

M= 8.6 X 10^–2 X 1000 g/mol / 250 g

M = 0.3264 kg/mol

CH₃CH₂CHClCOOH = CH₃CH₂CHClCOO^- + H ⁺

Initial moles

Equilibrium moles

(1-α)

Total moles at equilibrium = (1-α) + 2 α

= 1 + α

In order to find out the depression in freezing point,

values of i(vant Hoff’s factor) and α(degree of dissociation) are to be found out.

To find out degree of dissociation, _α

∴ i = 1.0654

Now, to find out the depression in freezing point,

Q: 19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.00 C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.

Given- w₁ = 500g

W₂ = 19.5g

K_f = 1.86 K kg mol^-1

Molar mass of CH₂FCOOH = 12 + 2 + 19 + 12 + 16 + 16 + 1

= 78 g mol^-1

The depression in freezing point is calculated by,