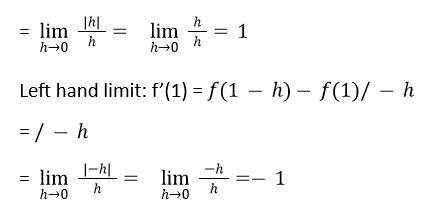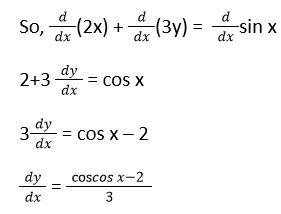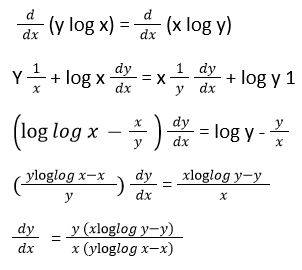Differentiation rules govern the differentiation process in the questions. These Differentiation rules are the material which builds the foundation to learn problem solving related to various topics . Students can access rules and conditions that allows differentiation of any function. Student can check Class 12 Continuity and Differentiability chapter for better understanding of the topic.
- What are Differentiation Rules?
- Differentiation Rules
- Weightage of Differential Rule in Class 12
- Illustrated Examples in Differential Rules
- FAQs on Differential Rules
What are Differentiation Rules?
Differentiation is the process of finding the derivatives of a function. In Mathematics, it is defined as the derivative of a function for an independent variable.
Some of the basic differentiation formulas are stated below:
| Function f(x) = y | Differentiation of function f’(x) = dy/dx |
|---|---|
| xn | nxn-1 |
| ex | ex |
| ln(x) | 1/x |
| Sin x | Cos x |
| Cos x | -sin x |
| Tan x | sec2x |
| K (constant) | 0 |
Differentiation Rules
Sum and Difference Rule:
The derivative of a function is the sum of the differences of the single function, which is
F(x) = u(x) + v(x)
Product Rule:
In this rule, one function f(x) is the product of two functions u(x) and v(x), and the derivative of a function is
F(x) = u(x) * v(x)
Then f’(x) = u’(x) * v’(x) + u’(x) * v’(x)
Quotient Rule:
In this rule, the function f(x) is in the form of two functions [u(x)]/[v(x)], the derivative of function is
F(x) = u’(x) * v’(x) - u’(x) * v’(x)/(v(x))2
Chain Rule:
In chain rule, the derivative of the function y = f(x) = g(u) and if u = h(x), then
Power Rule:
If x is a variable and y is another variable in the power rule, then the rate of change of x with respect to y is given by dy/dx.
Weightage of Differential Rule in Class 12
Chapter Continuity and Differentiability includes the topic of differential rules. The students learn about differentiating certain functions like polynomial and trigonometric functions and various differentials rules.
Illustrated Examples in Differential Rules
1. Prove that the function f given by
f(x) = | x – 1|, x ∈ R
is not differentiable at x = 1.
Solution:
Given, f(x) = | x – 1|
Then f(1) = |1 - 1| = 0
Right hand limit: f’(1) = f1+h-f1/h
= /h
Left hand limit ≠ Right hand limit.
2. Find dy/ dx in the 2x + 3y = sin x
Solution:
Given, 2x + 3y = sin x
3. Find dy/ dx in the yx = xy
Solution:
Given, yx = xy
logxy = log yx
y log x = x log y
FAQs on Differential Rules
Q: Define Differentiation?
Q: What is a linear and non-linear function?
In the linear function, the overall rate of change of the function is the same as the rate of change of a function at any point.
Non- Linear Function-
In the Non- Linear function, the rate of change varies from point to point.
Q: What is the meaning of continuity of a function?
Q: What is the constant rule of differentiation?
Q: What is the product rule of differentiation?
F(x) = u(x) * v(x).
Explore exams which ask questions on Maths Differentiation
Select your preferred stream
Maths Differentiation Exam
Student Forum
Other Topics under this Chapter
Other Class 12th Maths Chapters
- Quantitative Aptitude Prep Tips for MBA
- Maths Integrals
- Maths Differential Equations
- Maths Vector Algebra
- Maths Matrices
- Maths Determinants
- Maths Inverse Trigonometric Functions
- Maths Differentiation
- NCERT Class 12 Maths
- Maths Continuity and Differentiability
- Maths Applications of Derivatives
- Maths Application of Integrals
- Maths Linear Programming
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test