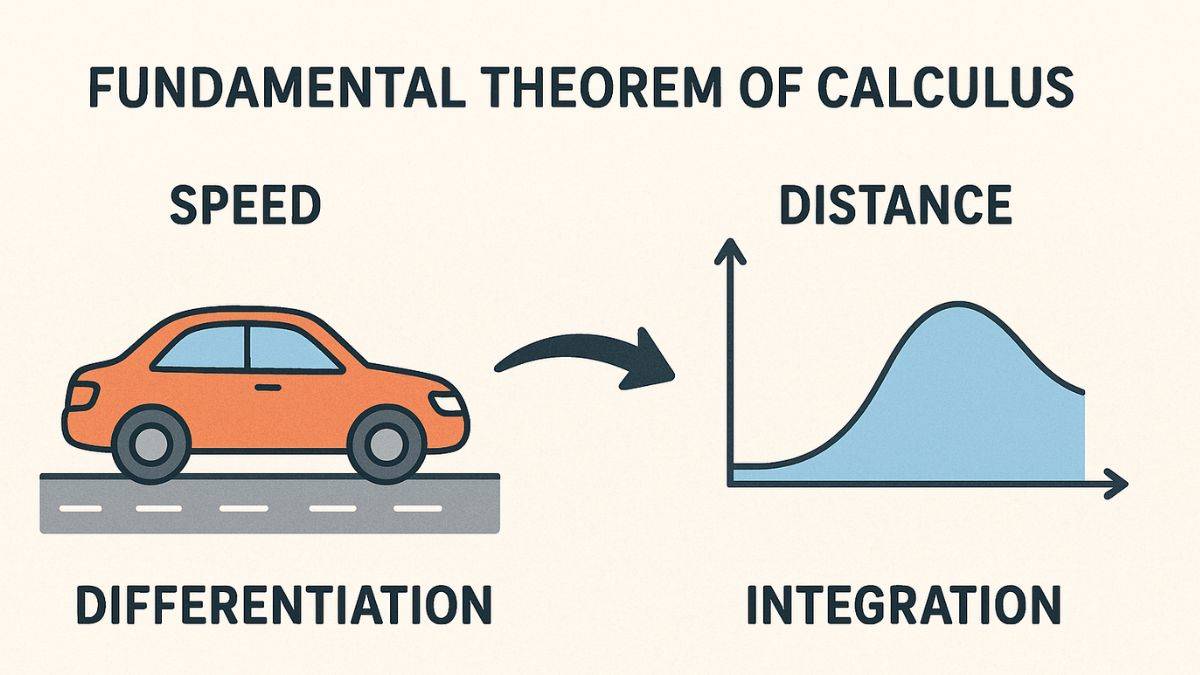
Imagine you are travelling in a car. You can know how far you have travelled in total (that's integral) with the help of the car speed at every moment (that's differentiation). Also, you can figure out the speed of the car by checking how fast the distance changes. We can also explain this situation with the help of the fundamental theorem of calculus. It corelate the differentiation and integration as two sides of the same coin.
The fundamental theorem of calculus tells us that we don't have to use an integral to calculate the total distance; applying an antiderivative can give the answers directly.
We can say that the fundamentals of calculus is the bridge that connects the world of "rate of change" to the world of "totals". It is useful in solving complex problems in Mathematics, Physics, Engineering, and everyday life much simple and more meaningful.
Important Topics:
| NCERT Class 11 notes | |
| Class 11 Chemistry notes |
- Define Fundamental Theorem of Calculus (FTC)
- Fundamental Theorem of Calculus
- How to Calculate Definite Integral?
- Tips For Exam Preparation
- NCERT Notes for Class 12 Maths
- NCERT Solutions for Class 12 Maths
Define Fundamental Theorem of Calculus (FTC)
The fundamental theorem of calculus (FTC) helps to correlate that differentiation and integration are inverse operations of each other. There are two parts:
1. The derivative of an integral gives back the original function if the function is continuous.
2. To find the definite integral of a function over an interval [a,b], we have to consider the difference of its antiderivative at the endpoints.
Important Link:
| NCERT Class 12 notes | |
| Class 12 Maths notes |
Fundamental Theorem of Calculus
As per the fundamental theorem of calculus, differentiation and integration are part of the same coin. Differentiation is used to break the function into small parts, while integration adds these parts to find the total.
The fundamental theorem of calculus has two parts: the first fundamental theorem of calculus and the second fundamental theorem of calculus. Below is a detailed description of these parts of the fundamental theorem of calculus.
- First Fundamental theorem of calculus:
- According to this theorem, the derivative of an integral is the original function. Suppose that you are walking along a path and recording the speed of your movement with each step taken. This is your function f(x). Now, calculate all speed values from the initial point to your endpoint; that's the total distance covered by you (integral). According to the fundamental theorem of calculus (FTC), if we check how fast the total distance is changing at any point, the result will be the speed again (differentiation).
- Second Fundamental Theorem of Calculus:
- According to the second FTC, the integration over an interval is the difference of antiderivatives at the end endpoint.
Also Read: NCERT Notes
The FTC is fundamental to calculus because it allows us to solve a wide range of problems involving rates of change, areas, and accumulation.
Let f(x) be a continuous function defined on an interval [a, b], and F(x) be the primitive or antiderivative of f(x), i.e., = F(x) or = f(x) or Then, the definite integral of f(x) over the interval [a, b] is denoted by and is given by
= F(b) – F(a)
F(b) – F(a) is also denoted by
Thus ……………………..(1)
Here, a is called the lower limit or inferior limit, and b is called the upper limit or superior limit. The value of a definite integral of a function is unique, and it does not depend on different forms of indefinite integrals. For if
= F(x) + c, even then
= = = F(b) – F(a)
Thus, the value of is the same even if we take = F(x) + c.
Example: Find
= sinx
= = sin – sin 0 = 1 – 0 = 1
Thus, while evaluating a definite integral, we need not add a constant of integration in the indefinite integral. The definition of definite integral is true only for functions which are continuous at a and b.
In fact, if = F(x), then
= = –
1. If F(x) is continuous at x = a and x = b, then
= F(b) – F(a)
2. If F(x) is discontinuous at x = a and x = b, then
= F(b) –
3. If F(x) is continuous at x = a and discontinuous at x = b, then
= – F(a)
Concepts Involved
1. is read as the definite integral of f(x) from a to b.
2. can be evaluated even if f(x) is not defined at a or b or both a and b.
3. We shall see that can be evaluated even if f(x) is not defined or discontinuous at a finite number of points in [a, b].
How to Calculate Definite Integral?
Problems in which an integral can be found by direct use of standard formulas or by the Transformation Method.
Working Rule:
- Find the indefinite integral without adding a constant c.
- Then, put the upper limit b in place of x and the lower limit a in place of x and subtract the second value from the first. This will be the required definite integral.
Example: Find .
Solution: dx = 4. + 3. – 2. + x
= x4 + x3 – x2 + x
= (14 + 13 – 12 + 1) – (0 + 0 – 0 + 0) = 2 – 0 = 2
Problems in which integral can be found by Substitution Method
Working Rule:
1. When an indefinite integral is to be found by substitution, then change the lower and upper limits of integration. If substitution is z = (x) and the lower limit of integration is a and the upper limit is b, then the new lower and upper limits will be (a) and (b), respectively.
2. Use the suitable substitution z = (x) and find the indefinite integral in terms of z.
Resubstitute for the new variable z and write the answer in terms of the original variable x. Now, find the final answer by putting upper and lower limits.
Example: Find the value of dx
Solution: Let z = 1 + sinx, then dz = cosx dx
When x = 0 , z = 1 + sin 0 = 1 + 0 = 1
And when x = , z = 1 + sin = 1 + 1 = 2
Now, dx = = dz
= = – = – =
Problems in which an integral can be found by the Method of Integration by Parts
Working Rule:
1. First, find the indefinite integral and then put the limits.
2. Find the integral using the formula for integral by parts and put the limits in the first part. In the next step, find the integral of the second part and then put the limits.
Example: Find the value of dx
Solution: dx = dx = dx – dx
= –
= + .
= . =
I = dx =
=
= 0 + =
Tips For Exam Preparation
- is read as the definite integral of f(x) from a to b.
- can be evaluated even if f(x) is not defined at a or b or both a and b.
- We shall see that can be evaluated even if f(x) is not defined or discontinuous at a finite number of points in [a, b].
Also Read: NCERT Solution for class 11 & 12
NCERT Notes for Class 12 Maths
| Chapter No. | Chapter Notes |
|---|---|
| 1 | Relations and Functions |
| 2 | Inverse Trigonometric Functions |
| 3 | Matrices |
| 4 | Determinants |
| 5 | Continuity and Differentiability |
| 6 | Application of Derivatives |
| 7 | Integrals |
| 8 | Application of Integrals |
| 9 | Differential Equations |
| 10 | Vector Algebra |
| 11 | Three-Dimensional Geometry |
| 12 | Linear Programming |
| 13 | Probability |
NCERT Solutions for Class 12 Maths
Maths Integrals Exam
Student Forum
Other Topics under this Chapter
- Integration
- Integrals
- Integration Rules
- Integration by Parts
- Integration by Substitution
- Application of Integrals
- Differentiation and Integration
- Line Integral
- Riemann Integral
- Surface Integral
- Integration as Inverse Process of Differentiation
- Fundamental Theorem of Calculus
- Methods of Integration
- Some Properties of Definite Integrals
- Definite Integrals
Other Class 12th Maths Chapters
- Quantitative Aptitude Prep Tips for MBA
- Maths Integrals
- Maths Differential Equations
- Maths Vector Algebra
- Maths Matrices
- Maths Determinants
- Maths Inverse Trigonometric Functions
- Maths Differentiation
- NCERT Class 12 Maths
- Maths Continuity and Differentiability
- Maths Applications of Derivatives
- Maths Application of Integrals
- Maths Linear Programming
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test