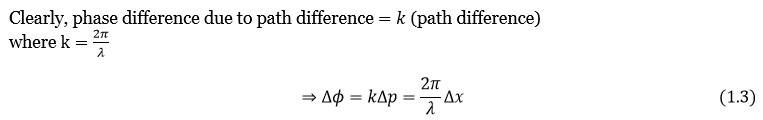Principle of Superposition: Definition, Formula, Types, and Conditions

Superposition of waves tells us what happens when two waves pass through the same medium at the same time. When the waves overlap, they combine to form a new, resultant wave. Now, this resultant wave has the displacement at every point to be the vector sum of the displacements of both waves at that specific point.   

Section 14.5 of Class 11 Physics Chapter 14 describes the principle of superposition like this 

"When the pulses overlap, the resultant displacement is the algebraic sum of the displacement due to each pulse. This is known as the principle of superposition of waves. According to this principle, each pulse moves as if others are not present. The constituents of the medium, therefore, suffer displacements due to both and since the displacements can be positive and negative, the net displacement is an algebraic sum of the two."

Simple Explanation

The principle of superposition states that when two or more waves traverse the same medium at the same time, the total displacement at any point and time is the algebraic sum of the displacements caused by each wave alone.

Mathematically, for two waves with displacements, represented as y₁(x,t) and y₂(x,t), we get the sum as below. This is also known as the Superposition of waves Formula. 

y(x,t) = y₁(x,t) + y₂(x,t)

Note that the superposition principle holds true if the dynamics remain linear. Otherwise, it will fail.  

Consider superposition of two sinusoidal waves (having same frequency), at a particular point.
Let, $x_1\left(t\right)=a_1\mathrm{s}\mathrm{i}\mathrm{n}\omega t$
and, $\mathrm{}{x}_2\left(t\right)=a_2\mathrm{s}\mathrm{i}\mathrm{n}(\omega t+\varphi )$
represent the displacement produced by each of the disturbances. Here we are assuming the displacements to be in the same direction. Now according to superposition principle, the resultant displacement will be given by,

$\begin{array}{rr}x\left(t\right)& =x_1\left(t\right)+x_2\left(t\right)\\ & =a_1\mathrm{s}\mathrm{i}\mathrm{n}\omega t+a_2\mathrm{s}\mathrm{i}\mathrm{n}(\omega t+\varphi )\end{array}$

where $A^2=a_1^2+a_2^2+2a_1\cdot a_2\mathrm{c}\mathrm{o}\mathrm{s}\varphi$
and $\mathrm{t}\mathrm{a}\mathrm{n}{\varphi }_0=\frac{a_2\mathrm{s}\mathrm{i}\mathrm{n}\varphi }{a_1+a_2\mathrm{c}\mathrm{o}\mathrm{s}\varphi }$

 

Let us explain the principle of superposition in mathematical terms. You can further go back to brush up on learning the displacement relation to understand this part better. 

Step 1: Write down each wave’s equation

Pick two sinusoidal waves travelling in the same direction (same k and ω), but possibly different amplitudes and phases:

$$\begin{array}{c}{y}_1(x,t)=A_1\sin (kx-\omega t+{\phi }_1)\\ y_2(x,t)=A_2\sin (kx-\omega t+{\phi }_2)\end{array}$$ Step 2: Invoke linearity of the wave equation $$\text{The wave equation governing}y(x,t)\text{is linear. That means if each of}{y}_1\text{and}{y}_2\text{individually satisfies the equation, then any sum}$$ $$y(x,t)=y_1(x,t)+y_2(x,t)$$

also satisfies it exactly.

3. Interpret at a fixed point PPP

Imagine standing at a fixed x=P. At time t, the medium “would” be at

$$\begin{array}{c}{y}_1(P,t)\text{if only wave 1 were present,}\\ y_2(P,t)\text{if only wave 2 were present.}\end{array}$$ Since the medium doesn’t “care” which wave caused the displacement, but only the net force, it simply reaches the sum:

$$y(P,t)=y_1(P,t)+y_2(P,t)$$

The following are the different types of superposition of waves.

• Constructive Interference: Whenever 2 waves are travelling in the same direction and are in phase with one another, the amplitude of those waves get added and a resultant wave is obtained. This is known as constructive interference.
• Destructive Interference: Destructive interference happens when two waves arrive out of sync so that a “hill” (crest) of one lines up with a “valley” (trough) of the other. At that moment, their pushes and pulls are opposite, and they cancel each other out which makes the combined wave smaller or even perfectly flat.

To advance with the superposition of waves principle, we need to dig a little deeper into interference patterns and differences in the paths the waves take. 

Let ${\mathrm{S}}_1$ and ${\mathrm{S}}_2$  be two sources producing progressive waves (disturbance travelling in space given by ${\mathrm{y}}_1$  and ${\mathrm{y}}_2$  )
At point $P$ ,

$y_1=a_1\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t-k{x}_1+{\theta }_1\right)$

$y_2={\mathrm{a}}_2\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t-k{x}_2+{\theta }_2\right)$

$y=y_1+y_2=A\mathrm{s}\mathrm{i}\mathrm{n}(\omega t+\mathrm{\Delta }\varphi )$

Here, the phase difference,

$\mathrm{\Delta }\varphi =\left(\omega t-k{x}_1+{\theta }_1\right)-\left(\omega t-k{X}_2+{\theta }_2\right)$

$=\mathrm{k}\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)+\left({\theta }_1-{\theta }_2\right)=\mathrm{k}\mathrm{\Delta }\mathrm{p}-\mathrm{\Delta }\theta$

where $\mathrm{\Delta }\theta ={\theta }_2-{\theta }_1$

Also, here $\mathrm{\Delta }p=\mathrm{\Delta }x$ is the path difference

In Figure 1.3, we can see this