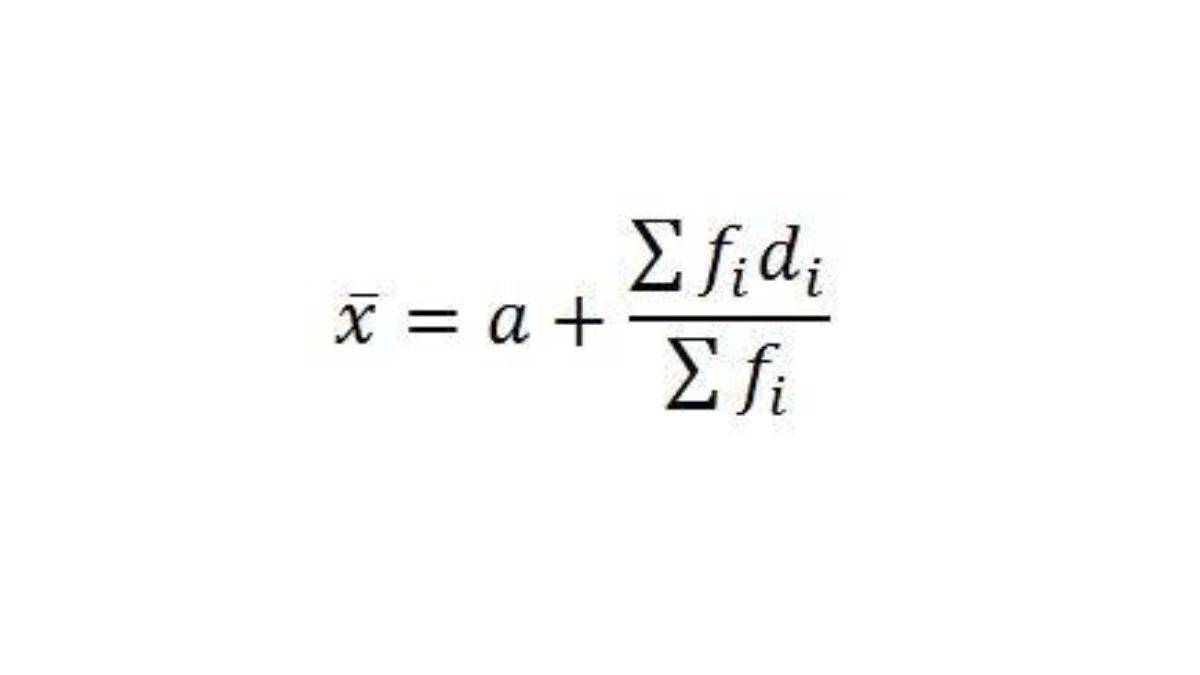Assumed Mean Method: Definition, Formula, Notes & Solved Examples

Updated on Jun 16, 2025 12:50 IST

The Assumed Mean Method is a technique in statistics to calculate the arithmetic mean (average). It is used to calculate large groups of data with large numerical values. In the assumed mean method, the mean value of the data is not calculated; instead, an assumed mean value is taken, and calculation is done around it. This process makes the calculation easy and reduces calculation errors.

The assumed mean method is an important topic in Class 11 Maths Chapter 13 Statistics. Students can check the NCERT Class 11 Math book for example problems based on the assumed mean method. The experts at Shiksha have prepared the Class 11 Math Statistics NCERT Solution to help students prepare for the exam. NCERT solutions are considered the best study materials to prepare for the board exam. Practising numerical questions based on the assumed mean method will help to understand the topic. Having a good command of statistical techniques to calculate and represent large data effortlessly. Check the article for detailed knowledge on the assumed mean method.

Table of contents

What is Assumed Mean Method?
How To Calculate The Assumed Mean?
Weightage of Assumed Mean
Illustrated Examples on Assumed Mean
FAQs on Assumed Mean Method

What is Assumed Mean Method?

Assumed mean methods are used to calculate the arithmetic mean (average). This method is applicable to large data sets. Using assumed mean methods makes the calculation easy, and the probability of calculation error is lower.

How To Calculate The Assumed Mean?

The assumed mean (a) is the arithmetic mean of grouped data. This method is suggested for large data samples. It is used to calculate the standard deviation of a data set. It is suitable for calculating the mean or average for tables involving largely spaced limits. It can be calculated by the following formula given below.

Also Check: Class 12 Math NCERT Solutions | NCERT Solution Class 11 Maths

How to calculate assumed mean?

Let x1,x2,x3,...,xN be the midpoints of ‘n’ class intervals and f1, f2, f3,..., fN be the respective frequencies of these class intervals. The assumed mean can be any Xi that is the midpoint of any class. Any Xi can be assumed as an assumed mean.

Assumed Mean Method Formula

Where,
a - assumed mean
Fi- Frequency of ith class
Di=xi-a= deviation of ith class
Fi= n summation of observations
Xi=class mark= (upper class limit+lower class limit)/2

Weightage of Assumed Mean

This topic is taught 11 standard and has about 15% weightage on an overall basis. In higher classes, too, this concept of statistics has immense use. Students must focus on the topic as it is has much importance when it comes to calculate a large set of data.

Illustrated Examples on Assumed Mean

1. The following table gives information about the marks obtained by 110 students in an examination:

Class	0-10	10-20	20-30	30-40	40-50
Frequency	3	20	26	36	25

Find the mean marks of the students using the assumed mean method.

Solution.

Class (CI)	Frequency (fi)	Classmark (xi)	fiXi
0-10	3	5	15
10-20	20	15	300
20-30	26	25	650
30-40	36	35	1260
40-50	25	45	1125
Total	Σfi =110		Σfixi = 3350

Mean of the data=FiXi/Fi
= 3350/110
= 34.5

2. The table below gives information about the percentage distribution of female employees in a company of various branches and several departments.

Percentage of female employees	Number of departments
5-15	3
15-25	7
25-35	5
35-45	2
45-55	8

3. Find the mean percentage of female employees.

Solution.

Percentage of female employees (CI)	Number of departments (fi)	Classmark (xi)	FiXi
5-15	3	10	30
15-25	7	20	140
25-35	5	30	60
35-45	2	40	80
45-55	8	50	400
Total	Σfi =25		FiXi= 710

Mean = (Σfixi /Σfi)
=710/25
= 28.4

4. A group of students surveyed as a part of their environmental awareness.

Number of plants	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10	10 - 12	12 - 14
Number of houses	1	2	1	5	6	2	3

The program in which they collected the following data regarding the number of plants in 20 homes in a locality. Find the mean number of plants per household using the assumed mean method.

Solution.

No. of Plants	No.of houses (Fi)	Xi	Di= Xi - a	FiDi
0-2	1	1	1-7=-6	-6
2-4	2	3	3-7=-4	-8
4-6	1	5	5-7=-2	-2
6-8	5	7=a	7-7=0	0
8-10	6	9	9-7=2	12
10-12	2	11	11-7=9	18
12-14	3	13	13-7=6	18
	Σfi =20			Σfidi = 32

Mean = a+ (Σfidi /Σfi)
= 7+(32/20)
=7+(8/5)
=8.6

FAQs on Assumed Mean Method

Q: What is the definition of an assumed mean method?

A: In statistics, the assumed mean is a method for calculating the arithmetic mean and standard deviation of a data set.

Q: How is the assumed mean method better than the ordinary mean method?

A: This method is recommended for large data values. It provides the arithmetic mean of grouped data.

Q: Should I always use the middle Xi as the assumed men in the assumed mean method?

A: There is no mandatory rule to use only the mid values of Xi as assumed mean. You can even have the lowest or highest Xi as your assumed mean.

Q: How do I calculate the classmark for the assumed mean method and Step deviation method?

A: The classmark is equal to the average of the sum of the lower and upper limits of a class.

Q: What are the methods to calculate the mean of a given frequency?

A: There are many methods to calculate the mean, but the most prominent ones are a direct method, assumed mean method, and step deviation method.
The direct method can be used for classes with small frequencies and class marks. Assumed mean and step deviation can be used for large data structures.