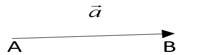Basic Concepts of Vector: Overview, Questions, Preparation

Problems based on classifying physical quantities into scalar and vectors

Working Rule:

Use the following results whichever is required.

1. A physical quantity is a scalar if it has only magnitude.
2. A physical quantity is a vector if it has magnitude as well as direction.

 

Problems based on graphical representation of a vector

Working Rule:

1. Choose a suitable scale and find the length of line segment representing the magnitude of the given vector.
2. Find the direction of the given vector.

Problems based on equal vectors collinear vectors and coinitial vectors

Working Rule:

Use the following results whichever are required.

1. Vectors $\vec{a}$ and $\vec{b}$ are collinear or parallel.

$\iff$ $\vec{a}$ = t $\vec{b}$ , where t is a scalar.

Parallel vectors may have same or opposite directions.

2. Two vectors are equal iff they have same magnitude and direction.
3. Two or more vectors are coinitial vectors if they have the same initial point.
4. $\left|t\vec{a}\right|$ $\left|t\right|\left|\vec{a}\right|$ , where t is a scalar.

Problems based on sum and difference of vectors

Working Rule:

Use the following results whichever is needed.

1. $\overrightarrow{AB}$ + $\overrightarrow{BC}$  = $\overrightarrow{AC}$

[Here terminal point of vectors  $\overrightarrow{AB}$  is B and initial point of vector $\overrightarrow{BC}$  is B.]

How to remember: A $\vec{B}$  + $\vec{B}$  C= $\overrightarrow{AC}$     (remove B)

In general vector sum of any two paths to go from one point to another are equal.

2. $\overrightarrow{AB}$ – $\overrightarrow{AC}$  = $\overrightarrow{CB}$

[Here initial point of vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$  are same]

How to remember: A $\vec{B}$ – $\vec{A}$ C= $\overrightarrow{CB}$      (remove A and reverse the order of B and C)

3. Resultant of a number of vectors is equal to the sum of these vectors.
4. If $\stackrel{̂}{i}$ and $\stackrel{̂}{j}$  be the unit vectors along x and y – axis respectively, then unit vector along a line which makes an angle θ with the positive direction of x – axis in anti – clockwise direction is cos θ $\stackrel{̂}{i}$  + sin θ $\stackrel{̂}{j}$ .

If θ is made in clockwise direction then unit vector is cos θ $\stackrel{̂}{i}$  – sin θ $\stackrel{̂}{j}$ .

5. If $\overrightarrow{OA}$ = $\vec{a}$  , $\overrightarrow{OB}$ = $\vec{b}$ , then $\overrightarrow{AB}$   = $\overrightarrow{OB}$  – $\overrightarrow{OA}$ = $\vec{b}$  – $\vec{a}$

  $\overrightarrow{AB}$ = P.V. of B – P.V. of A

6. If P ≡ (x, y, z) then $\overrightarrow{OP}$ = x $\stackrel{̂}{i}$  + y $\stackrel{̂}{j}$  + z $\stackrel{̂}{k}$
7. If P ≡ (x₁, y₁, z₁) and Q ≡ (x₂, y₂, z₂)

Then, $\overrightarrow{PQ}$  = (x₂ – x₁) $\stackrel{̂}{i}$ + (y₂ – y₁) $\stackrel{̂}{j}$ + (z₂ – z₁) $\stackrel{̂}{k}$

Problems based on modulus and direction cosines of vectors

Working Rule:

Use the following results whichever is needed.

1. If $\vec{a}$ = x $\stackrel{̂}{i}$  + y $\stackrel{̂}{j}$  + z $\stackrel{̂}{k}$ , then $\left|\vec{a}\right|$  = $\sqrt[]{x^2+y^2+z^2}$
2. Unit vector along $\vec{a}$ = $\frac{\vec{a}}{\left|\vec{a}\right|}$  = $\frac{x}{\sqrt[]{x^2+y^2+z^2}}$ $\stackrel{̂}{i}$    + $\frac{y}{\sqrt[]{x^2+y^2+z^2}}$ $\stackrel{̂}{j}$  + $\frac{z}{\sqrt[]{x^2+y^2+z^2}}$ $\stackrel{̂}{k}$
3. Direction cosines of $\vec{a}$ = x $\stackrel{̂}{i}$  + y $\stackrel{̂}{j}$  + z $\stackrel{̂}{k}$  are:

$\frac{x}{\sqrt[]{x^2+y^2+z^2}}$ , $\frac{y}{\sqrt[]{x^2+y^2+z^2}}$ , $\frac{z}{\sqrt[]{x^2+y^2+z^2}}$

Also, direction ratios of vector x $\stackrel{̂}{i}$  + y $\stackrel{̂}{j}$  + z $\stackrel{̂}{k}$  are x, y, z and x, y, z are proportional to direction cosines.

4. If $\vec{\alpha }$ and $\vec{\beta }$ be the unit vectors along any two lines then $\vec{\alpha }$  + $\vec{\beta }$ and $\vec{\alpha }$  – $\vec{\beta }$  are the vectors along the line which bisects the angle between these two lines.

 

Problems based on equality and collinearity of vectors

Working Rule:

Use the following results whichever is required.

1. Two vectors $\vec{a}$ and $\vec{b}$  are equal.

$\iff$ they have same magnitude and direction.

2. Two vectors are equal iff they have same components.
3. Two vectors in terms of $\stackrel{̂}{i}$ , $\stackrel{̂}{j}$ and $\stackrel{̂}{k}$ are equal iff the coefficients of $\stackrel{̂}{i}$ ,  $\stackrel{̂}{j}$ and $\stackrel{̂}{k}$  in the two vectors are respectively equal.
4. Vectors $\vec{a}$ and $\vec{b}$ are parallel.

$\iff$ $\vec{a}$ = t $\vec{b}$ , where t is a scalar.

(i) If t > 0, then $\vec{a}$ and $\vec{b}$  have same direction. $\vec{c}$

(ii) If t < 0, then $\vec{a}$  and $\vec{b}$  have opposite directions.

5. (i) If $\vec{a}$ and $\vec{b}$  are non-parallel vectors, then

x₁ $\vec{a}$ + y₁ $\vec{b}$  = x_{2 $\vec{a}$}  + y₂ $\vec{b}$               x₁ = x₂ and y₁ = y₂

(ii) If $\vec{a}$ , $\vec{b}$ , $\vec{c}$  are non-coplanar vectors, then

x₁ $\vec{a}$ + y₁ $\vec{b}$  + z_{1 $\vec{c}$}  = x₂ $\vec{a}$ + y₂ $\vec{b}$  + z₂   $\vec{c}$         $\Rightarrow$      x₁ = x₂, y₁ = y₂ and z₁ = z₂

 

TIPS FOR EXAM PREPARATION

• Magnitude: This is the length or size of the vector. It tells you how "big" the quantity is. 
• Direction: This indicates the way the vector is pointing. It can be described by an angle or by specifying a direction relative to a coordinate system. 
• Representation: Vectors can be represented in various ways:
  1. Geometrically: As arrows with a specific length and direction. 
  2. As ordered pairs or triplets: For example, (2, 3) or (1, 4, -2). These represent components along different axes (like x and y, or x, y, and z). 

              4) If P ≡ (x, y, z) then $\overrightarrow{OP}$  = x $\stackrel{̂}{i}$ + y $\stackrel{̂}{j}$ + z $\stackrel{̂}{k}$

       5) If P ≡ (x₁, y₁, z₁) and Q ≡ (x₂, y₂, z₂)

                 Then $\overrightarrow{PQ}$ ,  = (x₂ – x₁) $\stackrel{̂}{i}$ + (y₂ – y₁) $\stackrel{̂}{j}$  + (z₂ – z₁) $\stackrel{̂}{k}$

             6) Vectors $\vec{a}$ and $\vec{b}$  are parallel.

             $\iff$ $\vec{a}$            = t $\vec{b}$ , where t is a scalar.

                          (i) If t > 0, then $\vec{a}$  and $\vec{b}$ have same direction.

                         (ii) If t < 0, then $\vec{a}$  and $\vec{b}$  have opposite directions.