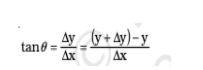Motion is the process of moving or changing the position of an object over time. It is a fundamental concept in classical mechanics. There are three types of motions: linear, rotatory, and oscillatory. Examples of motion are running, walking, closing doors, inhaling and exhaling air out of the lungs. In this article, we will derive three equations of motion by the calculus method.
Motion is an important topic in Class 11 Physics. The fundamentals of motion are also taught in Class 9 Science. JEE Main aspirants must focus on this topic. We have also provided NCERT Solutions for Class 11 Physics online. Students attempt the NCERT solutions to solve questions based on motion. Solving questions will build confidence and clarify the basic concepts.
Also Read: NCERT Solution for Class 12 Physics
- Equation of Motion
- Derivation of Equation of Motion
- Derivation of Equation of Motion by the Calculus Method
- Weightage in Class 11
- Illustrated Examples
- FAQs on Derive Equation of Motion by Calculus Method
Equation of Motion
The equation of motion determines the behavioural pattern of the physical system of the motion. It is part of a function of the equation of motion.
Broadly, there are three equations of motion, focusing on velocity, displacement, and acceleration.
Equations of motion:
- First equation – v = u + at
- Second equation – s = u + ½ at2
- Third equation – v2 = u2 + 2as
Derivation of Equation of Motion
The equation of motion can be derived using three methods,
- Simple algebraic method
- Graphical method
- Calculus method
Derivation of Equation of Motion by the Calculus Method
The equation of motion by calculus method can be determined, and velocity and acceleration can be identified. It is important for the understanding of physical quantities in motion.
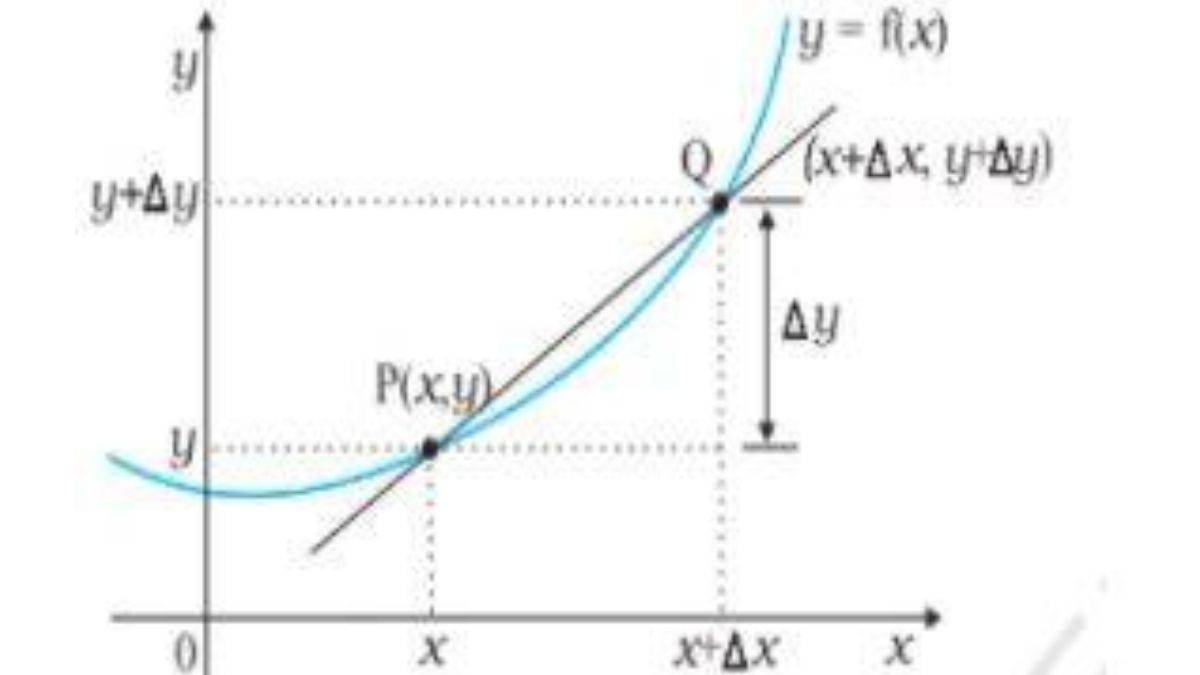
Let us make an equation using a quantity (y) and a single variable (x). it can be written as:
y = f (x)
Let’s take a step further and see the diagrammatic representation:
Image source - NCERT
P and Q are joined by a slope, and the equation of the slope is:
This is the equation by differential calculus.
- Derivation of the first equation
The rate of change of velocity is acceleration,
a = dv / dt
it can also be written as:
adt = dv
After integrating both equations, we get:
∫t0adt=∫vudv
at = v-u
After rearranging, we get,
| V = u + at |
First equation of motion by calculus methods.
- Derivation of the second equation
The change rate of displacement is velocity.
It can be equated as:
v = ds/dt
After rearranging we get,
ds = vdt
let’s integrate both the equations together,
ds = (u +at) dt
ds = (u +at) dt=(udt + atdt)
after simplifying it further, we get:
| = ut + ½ at2 |
- Derivation of the third equation
As we discussed earlier that the rate of change in velocity is called acceleration, and it is represented as follows:
a = dv/dt
as discussed in the second equation that the rate of change in displacement is velocity and is written as,
v = ds/dt
by multiplying both the above-written equation, we get,
a ds/dt = v dv/dt.
It can be rewritten as
| V2 = u2 +2as |
Weightage in Class 11
The chapter ‘Introduction to Motion’ holds a weightage of 5 marks in total. It consists of one short question of 2 marks and another short type question consisting of 3 marks.
Illustrated Examples
1. Explain the derived equation for the second equation of motion.
Derived equation for the second equation of motion is - V = ut + ½ at2
2. Explain the formula used in defining the third equation of motion.
Formula for the third equation of motion is – v2 = u2 + 2as
3. Provide an illustrated example of an object in a free-fall motion in which there is a variation of distance concerning time.
FAQs on Derive Equation of Motion by Calculus Method
Q: What’s the formula for the second equation of motion?
Q: What’s the derived equation of the first equation of motion?
Q: What are different methods that are used to derive motion equations?
- Simple algebraic method
- Graphical method
- Calculus method
Q: What are the main factors every equation of motion focuses on?
Q: Provide an example of motion in a free fall where velocity is variant.
Physics Motion Exam
Student Forum
Other Topics under this Chapter
- Rotation and Revolution
- Uniform and Non Uniform Motion
- Derivation of Centripetal Acceleration
- Derivation of Escape Velocity
- Drift Velocity Derivation
- Hubbles Law
- Kinematics of Machines
- Kinematics Equations of Motion
- Derivation of Compton Effect
- Derive Equation of Motion by Calculus method
- Terminal Velocity derivation
- Centripetal and Centrifugal Force
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test