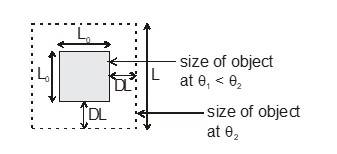
Most of the materials expand when their temperature is increased. Rails roads tracks, bridges all have some means of compensating for thermal expansion. When a homogeneous object expands, the distance between any two points on the object increases. Figure shows a block of metal with a hole in it. The expanded object is like a photographic enlargement. That in the hole expands in the same proportion as the metal, it does not get smaller
At the atomic level, thermal expansion may be understood by considering how the potential energy of the atoms varies with distance. The equilibrium position of an atom will be at the minimum of the potential energy well if the well is symmetric. At a given temperature each atom vibrates about its equilibrium position and its average remains at the minimum point. If the shape of the well is not symmetrical the average position of an atom will not be at the minimum point. When the temperature is raised the amplitude of the vibrations increases and the average position is located at a greater inter atomic separation. This increased separation is manifested as expansion of the material. Almost all solids and liquids expand as their temperature increases. Gases also expand if allowed. Solids can change in length, area or volume, while liquids change in their volumes.
Please note that Thermal Properties of Matter is an important chapter for class 12th students and practicing NCERT solutions of Thermal Properties of Matter will be helpful from examination point of view.
- What is Thermal Expansion: Class 11 NCERT Definition
- Thermal Expansion Formula
- Coefficient of Thermal Expansion: Meaning & Units
- Coefficient of Thermal Expansion Formula
- Linear Expansion
- Thermal stress of a material
- Variation of time period of pendulum clocks
- Measurement of length by metallic scale
- Superficial or Areal Expansion
- Volume or Cubical Expansion
- Variation of Density with Temperature
- Apparent Expansion of a Liquid in a Container
- Variation of Force of Buoyancy with Temperature
- Bimetallic Strip
- Applications of Thermal Expansion
- Factors Affecting Thermal Expansion
What is Thermal Expansion: Class 11 NCERT Definition
According to NCERT, Thermal Expansion definition is as follows:
“It is our common experience that most substances expand on heating and contract on cooling. A change in the temperature of a body causes change in its dimensions. The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion.“
Basically, expansion of the dimensions of a body due to an increase in temperature is called Thermal expansion.
Thermal Expansion Formula
The most common thermal expansion formula is the linear expansion law for solids, as stated below:
- ΔL = change in length
- L0 = original length
- ΔT = temperature change (Tfinal – Tinitial)
- α = coefficient of linear thermal expansion
Please remember that this is important for JEE Mains exams aspirants and they should be well-versed in the concepts related to Thermal Expansion.
Coefficient of Thermal Expansion: Meaning & Units
The coefficient of thermal expansion (often written as α) tells you how much a material grows (or shrinks) per degree of temperature change.
- Imagine a metal bar of length at temperature .
- Heat that bar by (say from 20 °C to 50 °C).
- Its new length will be slightly larger.
- The coefficient captures that tiny fractional growth:
- In plain terms, “for every 1 °C (or 1 K) increase, the bar’s length changes by times its original length.”
Coefficient of Thermal Expansion Formula
The linear thermal expansion formula tells you how much an object’s length changes when its temperature changes. There are two equivalent ways to write it:
1. Defining the Coefficient
Start with the fractional change in length per degree:
- = change in length
- = original length
- = temperature change
“The coefficient is the amount of length change, as a fraction of the original length, for each 1 °C (or 1 K) change in temperature.”
2. Predicting Length Change
Rearrange to find the actual change in length:
- Multiply the original length by the coefficient , then by how many degrees the temperature changes .
3. Step-by-Step Use
- Measure the object’s original length .
- Look up or measure its (units: 1 / °C or 1 / K).
- Compute .
- Plug in: .
- Add to the original: .
Linear Expansion
When the rod is heated, its increase in length is proportional to its original length and change in temperature where is in or K .
If
where is called the coefficient of linear expansion whose unit is or .
. Where is the length after heating the rod.
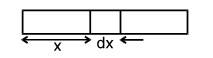
Variation of with temperature and distance
(a) If varies with distance, .
Then total expansion .
(b) If varies with temperature, . Then
Note : Actually thermal expansion is always 3-D expansion. When other two dimensions of object are negligible with respect to one, then observations are significant only in one dimension and it is known as linear expansion.
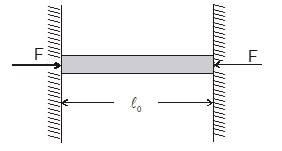
Thermal stress of a material
If the rod is free to expand then there will be no stress and strain. Stress and strain is produced only when an object is restricted to expand or contract according to change in temperature. When the temperature of the rod is decreased or increased under constrained condition, compressive or tensile stresses are developed in the rod. These stresses are known as thermal stresses.
Strain
Note : Original and final length should be at same temperature.
Consider a rod of length which is fixed between to rigid end separated at a distance now if the temperature of the rod is increased by then the strain produced in the rod will be :
is very small so
strain (negative sign in the answer represents that the length of the rod is less than the natural length that means is compressed by the ends.)
It is important to note that those who are going to take NEET exam and CBSE Board exam must learn both theoritical and practical aspects of this topic.
Variation of time period of pendulum clocks
The time represented by the clock hands of a pendulum clock depends on the number of oscillation performed by pendulum every time it reaches to its extreme position the second hand of the clock advances by one second that means second hand moves by two seconds when one oscillation in complete
Let at temperature and at temperature .
Therefore change (loss or gain) in time per unit time lapsed is gain or loss in time in duration
of ' t ' in
, if T is the correct time then
(a) clock becomes fast and gain time
(b) clock becomes slow and loose time
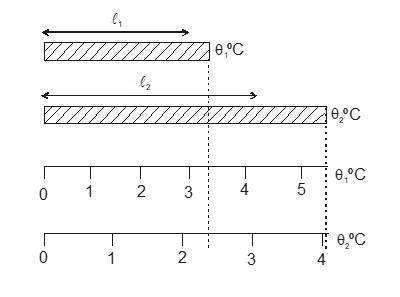
Measurement of length by metallic scale
Superficial or Areal Expansion
Volume or Cubical Expansion
Variation of Density with Temperature
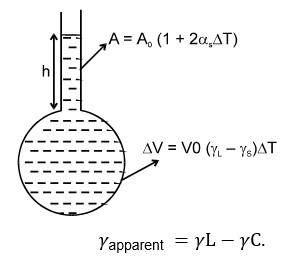
Apparent Expansion of a Liquid in a Container
Variation of Force of Buoyancy with Temperature
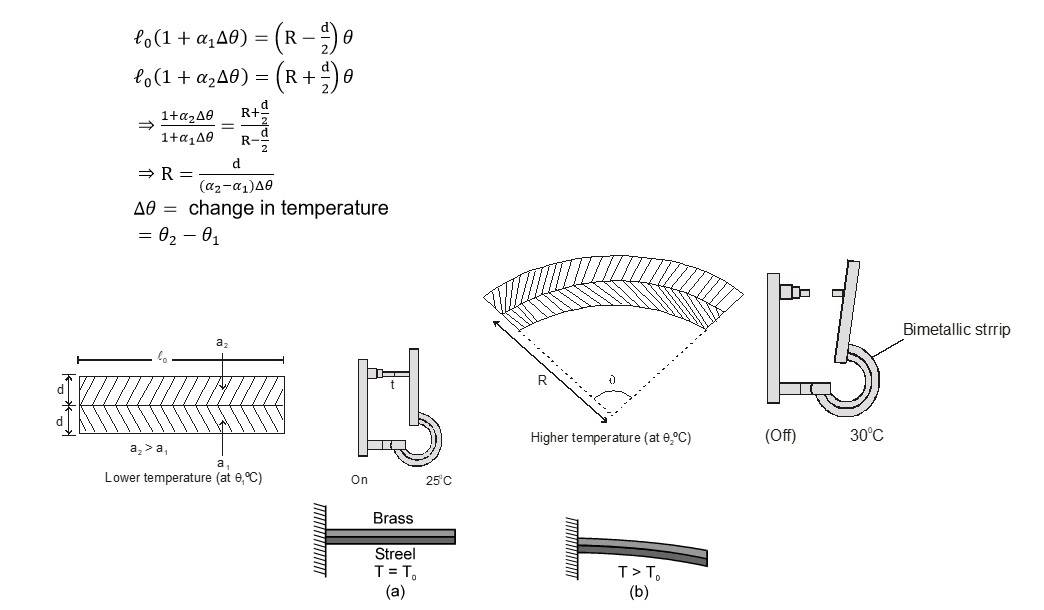
Bimetallic Strip
Applications of Thermal Expansion
Factors Affecting Thermal Expansion
Physics Thermal Properties of Matter Exam
Student Forum
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion