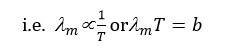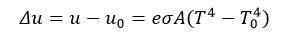Heat Transfer is the study of energy movement or transfer from one system to another without losing the energy in the surrounding system. Energy can transfer in three ways: conduction, convection, and radiation. Understanding the fundamentals of heat transfer mechanisms can help explain natural phenomena and improve the design of thermal systems such as heaters, insulators, radiators, etc.
Heat Transfer is an important topic in Class 11 Physics Chapter 10 Thermal Properties of Matter. Through this article, we have discussed the heat transfer definition and its types. Students can go through the article and understand the Class 11 Physics heat transfer topics in detail. Also, Class 11 Physics Chapter 10 NCERT solution for exercise problems is available online. Practice the NCERT Class 11 Physics Solutions to score good marks in the CBSE board exam. NCERT Solutions are considered the best study material to prepare for the exam. They consist of a number of questions based on the previous year CBSE board exam.
- What is Heat Transfer?
- Types of Heat Transfer
- Conduction
- Steady State
- Thermal Resistance to Conduction
- Slabs in Parallel and Series
- Slabs in Parallel
- Convection
- Radiation
- Prevost Theory of Exchange
- Perfectly Black Body and Black Body Radiation
- Absorption, Reflection and Emission of Radiation
- Kirchoff's Law
- Nature of Thermal Radiations : (Wien's Displacement Law)
- Stefan-Boltzmann’s Law
What is Heat Transfer?
We can explain heat transfer as the movement of thermal energy from one system to another or one part of the system to another due to a temperature difference. Every material has a different thermal conductivity.
Importance of Heat Transfer
Knowledge of heat transfer is important to maintain the balance in nature, designing machines and structures.
- Daily Life Application
- Ironing clothes, boiling water and cooking food all involve heat transfer.
- Controlling the heat transfer using insulation or ventilation can keep cool in summer and warm in winter.
- Engineering and Technology
- The proper functioning of engines, refrigerators and air conditioning depends on the heat transfer properties of the devices.
- We can control the overheating and damage of electronic devices through thermal management.
- Environmental Significance
- The heat transfer between earth, atmosphere, and oceans influences the weather patterns, oceans currents, and climate change.
- Medical and Biological Systems
- Regulation of human body temperature depends on the heat transfer through conduction, convection, and radiation.
- Incubators and heating pads use controlled heat transfer for patient care.
- Industrial Application
- Controlling heat transfer in power plants, chemical factories, and manufacturing industries can improve efficiency and safety.
Types of Heat Transfer
Heat is a form of energy that moves from a warmer object to a cooler one due to a temperature difference. This energy transfer can happen in three main ways:
- Conduction
- Convection
- Radiation
Conduction
Conduction is the process where heat travels through a material without the material itself moving. Imagine holding one end of a metal rod while the other end is in a flame. Eventually, your hand feels the heat, not because the metal moved, but because the energy passed from atom to atom.
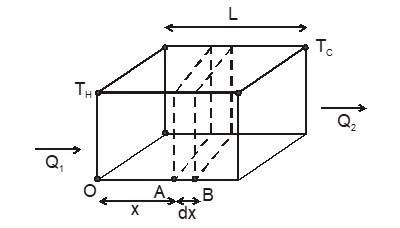
In solids, especially metals, atoms vibrate more intensely when heated. These vibrations are passed along to neighbouring atoms, transferring heat through the material. Let’s consider a flat slab with area A and thickness L, where one side is at a higher temperature (Tₕ) and the other at a lower temperature (T꜀). The heat flow Q through the slab over time t is
Steady State
If the temperature of a cross-section at any position x in the above slab remains constant with time (remember, it does vary with position x), the slab is said to be in steady state.
Remember steady-state is distinct from thermal equilibrium for which temperature at any position (x) in the slab must be same.
For a conductor in steady state there is no absorption or emission of heat at any cross-section. (As temperature at each point remains constant with time). The left and right face are maintained at constant temperatures respectively, and all other faces must be covered with adiabatic walls so that no heat escapes through them and same amount of heat flows through each cross-section in a given Interval of time.
Hence, . Consequently, the temperature gradient is constant throughout the slab.
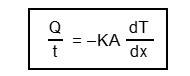
Hence,
= and .... (3.1)
Here, Q is the amount of heat flowing through a cross-section of the slab at any position in a time interval of t.
Thermal Resistance to Conduction
If you are interested in insulating your house from cold weather or for that matter, keeping the meal hot in your tiffin-box, you are more interested in poor heat conductors, rather than good conductors. For this reason, the concept of thermal resistance R has been introduced.
For a slab of cross-section A, Lateral thickness L and thermal conductivity K,
... (4.1)
In terms of R, the amount of heat flowing through a slab in steady-state (in time t)
If we name as thermal current iT
then, (4.2)
This is mathematically equivalent to OHM’s law, with temperature playing the role of electric potential. Hence, results derived from OHM’s law are also valid for thermal conduction.
Moreover, for a slab in steady state, we have seen earlier that the thermal current remains the same at each cross-section. This is analogous to Kirchhoff’s current law in electricity, which can now be very conveniently applied to thermal conduction.
Slabs in Parallel and Series
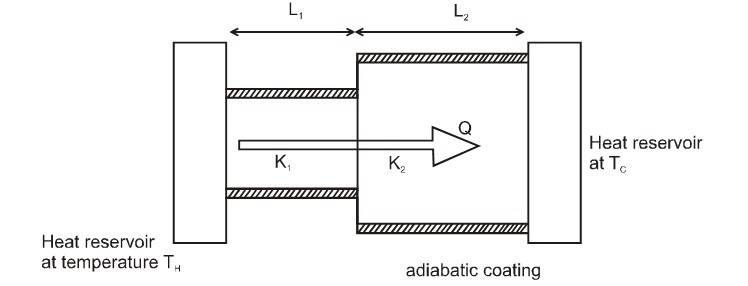
Slabs in series (in steady state)
Consider a composite slab consisting of two materials having different thicknesses and different thermal conductivities. The temperature at the outer surface of the slab is maintained at , and all lateral surfaces are covered by an adiabatic coating.
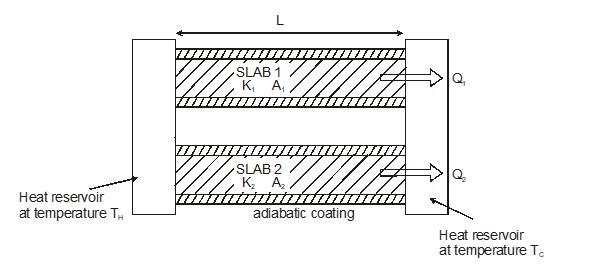
Slabs in Parallel
Convection
Radiation
Prevost Theory of Exchange
Perfectly Black Body and Black Body Radiation
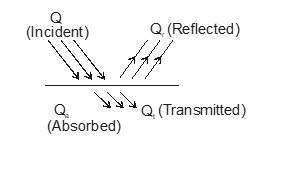
Absorption, Reflection and Emission of Radiation
Kirchoff's Law
Nature of Thermal Radiations : (Wien's Displacement Law)
Stefan-Boltzmann’s Law
Physics Thermal Properties of Matter Exam
Student Forum
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion

 ... (2.1)
... (2.1)
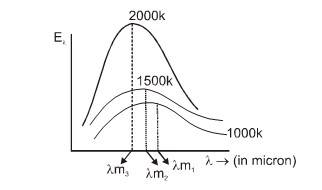
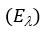 is maximum.
is maximum.