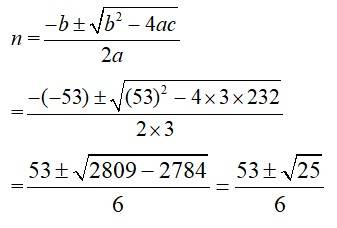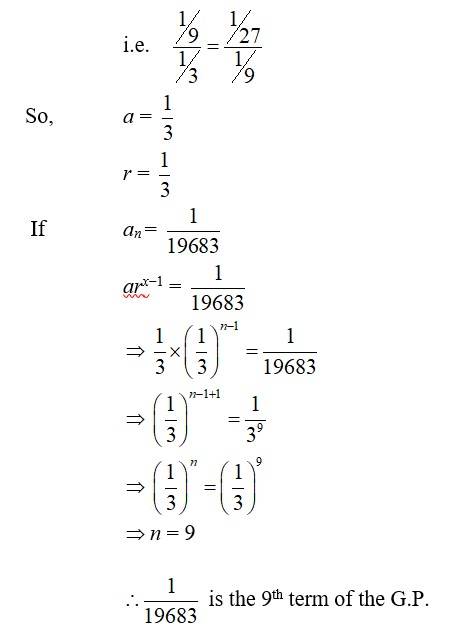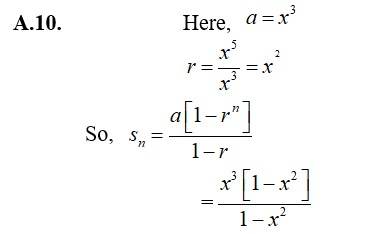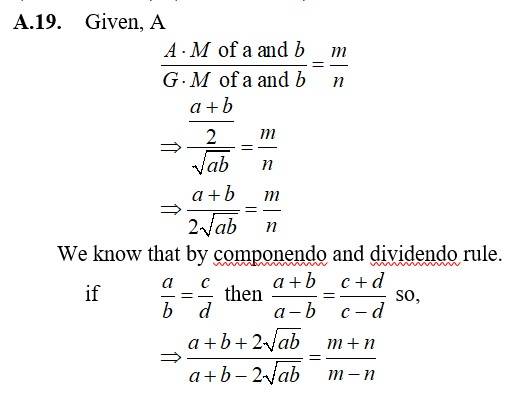Sequence and Series Class 11 NCERT Solutions cover sequences, which are used in the same way as it is in ordinary English. Here, if a collection of objects is listed in a sequence, it means that it is listed in a way where there is a first member, a second member, and so on. Sequences and Series Class 11 covers geometric mean, arithmetic mean, special series in the form of sum to n terms of consecutive natural numbers, and the relationship between A.M. and G.M., sum to n terms of cubes of natural numbers, and sum to n terms of squares of natural numbers.
It further covers sequences and series. Through these NCERT solutions, students get an effective study material which helps them to prepare for the Class 11 exams, CBSE exams, and other competitive tests like the JEE Main exam. In case you are looking for complete Class 11 Maths NCERT Notes designed for your exam preparation. Explore here - it will give you Class 11 Maths NCERT Notes with important notes and solved examples.
- A Quick Look at Class 11 Sequences and Series NCERT Solutions
- Class 11 Sequence And Series: Key Topics, Weightage
- Important Formulas of Sequence and Series Class 11 Mathematics
- Class 11 Sequence And Series NCERT Solution PDF: Download PDF for Free
- Class 11 Math Sequence And Series Exercise 8.1 Solutions
- Class 11 Math Sequence And Series Exercise 8.2 Solutions
- Class 11 Math Sequence And Series Exercise 8.3 Solutions
- Class 11 Math Sequence And Series Exercise 8.4 Solutions
- Class 11 Math Sequence And Series Miscellaneous Exercise Solutions
A Quick Look at Class 11 Sequences and Series NCERT Solutions
Here is an overview of the Sequences and Series Class 11 Solutions:
- Class 11 Sequence and Series NCERT Solutions chapter covers the meaning of sequence in mathematics. It means an arrangement of a number in a definite order. Also, it defines the sequence as a function.
- It covers finite and infinite sequences, finite series, geometric progression, and common ratio. Mathematically, the Geometric Progression is shown as:
Class 11 Sequence And Series: Key Topics, Weightage
Class 11 sequence and series is an important chapter in Mathematics. The key concepts to focus on are - Arithmetic Progression (AP), Harmonic Progression (HP), Geometric Progression (GP), Relationship between AM and GM, Special Series, and Arithmetico-Geometrical Progression (AGP). The chapter is significant in building a strong foundation as it is used in various other areas of mathematics. Students must focus on the formulas, definitions, and properties of different types of sequences and series. See below the topics covered in this Chapter:
| Exercise | Topics Covered |
|---|---|
| 8.1 | Introduction |
| 8.2 | Sequences |
| 8.3 | Series |
| 8.4 | Geometric Progression |
| 8.5 | Relationship Between A.M. and G. M. |
Sequences and Series Class 11 Maths Weightage in JEE Main Exams
| Exam | Number of Questions | Weightage |
|---|---|---|
| JEE Main | 2 questions | 6.6% |
Related Links
| NCERT Class 11 Notes | NCERT Notes for Class 11 & 12 | NCERT Solutions for Class 11 Maths |
Important Formulas of Sequence and Series Class 11 Mathematics
Sequence and Series Important Formulae for CBSE and Competitve Exams
Students can check the important formulae below;
Arithmetic Progression (AP):
- nth term:
- Sum of first n terms:
- Sum when last term is known:
- Number of terms in an AP:
Geometric Progression (GP):
- nth term:
- Sum of first n terms:
, if
- Sum of an infinite GP:
, if
Harmonic Progression (HP):
- nth term: , where is the nth term of the corresponding AP
- Harmonic Mean (HM) between two numbers:
-
Special Series:
- Sum of first n natural numbers:
- Sum of squares of first n natural numbers:
- Sum of cubes of first n natural numbers:
Class 11 Sequence And Series NCERT Solution PDF: Download PDF for Free
There is a link given below for students to download the free Sequence and Series Class 11 PDF. The Sequences and Series Class 11 includes clear and detailed solutions for NCERT textbook questions. The solutions are created by experts to boost students' confidence in solving the complex problems related to sequences and series.
Get the complete chapter-wise free PDFs and key topics of Class 11 and 12 for Maths, Physics, Chemistry here, based on the NCERT textbooks.
Class 11 Math Sequence and Series Solution PDF: Free PDF Download
Class 11 Math Sequence And Series Exercise 8.1 Solutions
Class 11 Sequence and Series Ex 8.1 focuses on the basics of sequences, types of sequences, and arithmetic progression (AP). Exercise 8.1 class 11 focuses on deriving the nth term of a sequence, identifying patterns, and calculating the sum of terms in an arithmetic progression. Candidates can check solutions to all 14 questions in ex 8.1 of class 11 below;
Sequence And Series Exercise 8.1 SolutionsWrite the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are: Q1. an = n (n + 2) |
| A.1. Here an = n (n + 2) Substituting n=1,2,3,4,5 we get, a1=1(1+2)=1 × 3=3 a2=2(2+2)=2 × 4=8 a3=3(3+2)=3 × 5=15 a4=4(4+2)=4 × 6=24 a5=5(5+2)=5 × 7=35. Hence, the first five terms are 3,8,15,24 and 35 |
| Q2. an= |
| A.2. Here, a1= Substituting n=1,2,3,4,5 we get,
. Hence the first five terns are and . |
| Q3. an=2n |
| A.3. Here an=2n Substituting n=1,2,3,4,5 we get, a1=21=2 a2=22=4 a3=23=8 a4=a4=16 a5=25=32. Hence the first five terns are 2,4,16,32 and 64. |
| Q4. |
| A.4. Here, Putting n=1,2,3,4,5 we get,
Hence, the first five terms are |
| Q5. an = (–1)n – 1 5n + 1 |
| A.5. Here, an=(–1)n – 1 . 5n+1 Putting n=1,2,3,4,5 we get, a1=(–1)1 – 1.51+1=(–1)0× 52=25 a2=(–1)2 – 1.52+1=(–1)1× 53= –125 a3=(–1)3 – 1. 53+1=(–1)2× 54=625 a4=(–1)4 – 1. 54+1=(–1)3. 55= –3125 a5=(–1)5 – 1. 55+1=(–1)4. 56=15625. Hence, the first five terms are 25, –125,625, –3125and 15625. |
| Q6. an = n |
| A.6. Here, an=n Putting n=1,2,3,4,5 we get,
Hence, the first five terms are . |
| Q7. an = 4n – 3; a17, a24 |
| A.7. an=4n – 3. Putting n=17, we get a17=4 × 17 – 3=68 – 3=65. and putting n=24 we get, a24=4 × 24 – 3= 96 – 3=93 |
| Q8. ; a7 |
| A.8. Put n=7,
|
| Q9. an = ( –1)n – 1n3; a9 |
| A9. an=( –1)n – 1 .n3. Put n=9 we get, aq=(–1)9 – 1.93=(–1)8. 729=729. |
| Q10. ;a20 |
| A.10. . Put n=20,
|
| Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain thecorresponding series: Q11. a1= 3, an= 3an – 1+ 2 for all n > 1 |
| A.11. Given, a1=3 an=3an – 1.+2 "n>1. Puttingn=2,3,4,5 we get, a2=3a2 – 1+2=3a1+2=3 × 3+2=9+2=11 a3=3a3 – 1+2=3a2+2=3 × 11+2=33+2=35 a4=3a4 – 1+2=3a3+2=3 × 35+2=105+2=107. a5=3a5 – 1+2=3a4+2=3 × 107+2=321+2=323. Hence, the first five terms of the sequence are 3,11,35,107,323. And the series is 3+11+35+107+323+ … |
| Q12. a1 = –1, |
| A.12. Given, a1= –1,
Putting n=2,3,4,5 we get,
. So the first five terms of the sequence are –1, and . And the series is . |
| Q13. a1 = a2= 2, an = an – 1–1, n > 2 |
| A.13. Given, a1=a2=2. an=an – 1 – 1 Putting n=3,4,5. a3=a3 – 1 – 1=a3 – 1 – 1=a2 – 1=2 – 1=1 a4=a4 – 1 – 1=a3 – 1=1 – 1=0 a5=a5 – 1 – 1=a4 – 1=0 – 1= –1 . Hence the first five forms of the sequence are 2,2,1,0, –1. And the series is 2+2+1+0+(–1)+ …. |
| Q14. The Fibonacci sequence is defined by 1 = a1 = a2 and an= an – 1 + an – 2, n > 2. Find , for n = 1, 2, 3, 4, 5. |
| A.14. Given, a1=1=a2. an=an – 1+an – 2,n>2. We need to find, Putting n=3,4,5,6 in an=an – 1+an – 2 we have, a3=a3 – 1+a3 – 2=a2+a1=1+1=2. a4=a4 – 1+a4 – 2=a3+a2=2+1=3. a5=a5 – 1+a5 – 2=a4+a3=3+2=5. a6=a6 – 1+a6 – 2=a5+a4=5+3=8. Now, to find , Substitute n=1,2,3,4,5.
. |
Commonly asked questions
35. The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Showthat q2 = ps.
35. Let a and r be the first term and the common ratio between G.P.
So, a5= p a rt-1 = p ar4 = p
a8 = q a r8-1 =q ar7= q
a11= r ar11-1 = r ar10= 5
So, L.H.S. q2 = (ar7)2 = a2r14
R.H. S. = p.s= (ar4) (ar)10 = a1+1 r4+10 = a2r14
L.H.S. = R.H.S.
63. What will Rs 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?
63. Given,
Principal value, amount deposited, P= ?500
Interest Rate, R= 10
Using compound interest = simple interest +
Amount at the end of 1st year
=
= ?500× (1.1)
Amount at the end of 2nd year
=
=
= ?500 (1.1)2
Similarly,
Amount at the end of 3rd year = ?500 (1.1)3
So, the amount will form a G.P.
? 500 (1.1)? 500 (1.1)2?500 (1.1)3, ……….
After 10 years = ?500 (1.1)10
32. The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120° , find the number of the sides of the polygon.
32. Let 'n' be the no. of sides of a polygon.
So, sum of all angles of a polygon with sides n
= (2n – 4) × 90°
= (n – 2) × 2 × 90°
= (n – 2)180°
As the smallest angle is 120° and the difference between 2 consecutive interior angle is 5°. We have,
a =120°
d =5°
So, sum of n sides =180° (n – 2).
n [240°+5°n – 5°]=360°n– 720°
n [5°n+235°]=360°n – 720°
5°n2+235°n=360°n – 720°
n2+47°n=72n – 144 [? dividing by 5]
n2+47n – 72n+144=0.
n2 – 25n+144=0
n2 – 9n– 16n+144=0
n (n – 9) –16 (n – 9)=0
(n – 9) (n – 16)=0
So, n=9,16.
When n=9,
the largest angle =a+ (9 – 1)d=120°+8 × 5° = 120° + 40° = 160°< 180°
Hence, n=9 is permissible
When n=16,
Lorgest angle =a+ (16 – 1)d=120°+15 × 5° = 120° + 75° = 195°> 180°.
which is not permissible as no angle in polygon can exceed 180°.
Hence, number of sides in polygon, n=9.
Class 11 Sequence And Series Exercise 8.2 Solution
15. Find the sum of odd integers from 1 to 2001.
15. Sum of odd integers from 1 to 2001
=1+3+5+ … +2001
So, a=1
d=3 – 1=2
? For nth term,
an=a+ (n – 1)d.
? the last nth term is 2001,
2001 =1+ (n – 1)2.
(n – 1)2 =2001 – 1
n – 1=
n =1000+1
n =1001.
? Sum of n terms, Sn= (a + l); l = last term.
? Required sum = =1002001
64. If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation.
64. Let a and b be the roots of quadratic equation
So, A.M = 8
a + b =16 ….I
G.M. =
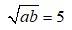
ab = 25…. II
We know that is a quadratic equation
(sum of roots) + product of roots = 0
using I and II
Which is the reqd. quadratic equation
4.
4. Here,
Putting n=1,2,3,4,5 we get,
Hence, the first five terms are
17. In an A.P., the first term is 2 and the sum of the first five terms is one-fourth ofthe next five terms. Show that 20th term is –112.
17. Given, a=2
Let A1, A2, A3, A4, A5, A6, A1, A6, A7, A10 be the first ten terms. So, A1=a.
Given A1+A2+A3+A4+A5= (A6+A1+A8+A1+A10)
a+ (a+d)+ (a+2d)+ (a+3d)+ (a+4d)
= [ (a+5d)+ (a+6d)+ (a+7d)+ (a+8d)+ (a+9d)]
5a+10d= [5a+35d].
4 [5a+10d]=9a+35d.
20a+40d=5a+35d.
40d – 35d=5a – 20a
5d= –15a
d= –3a
d= –3 * 2 [as a=2]
d= –6
So, A20=a+ (20 – 1)d
=2+19 * (–6)
=2 – 114
= –112.
18. How many terms of the A.P. – 6, , –5, …. are needed to give the sum –25?
18. Let the sum of n farms of the A.P –6, , –5, …. gives –25.
Then,
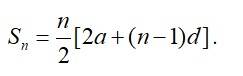
From the given A.P.
a= –6
d= –
So, –25=
–25 × 2=n
–50=n
–50=n
–50 × 2 =n[n – 25]=n2 – 25n
n2 – 25n+100=0.
n2 – 5n – 20n+100=0
n(n – 5) – 20(n – 5)=0
(n – 5)(n – 20)=0
So, n=5 and n=20.
When n=5
= –25.
When n=20
= = –120 + 19 × 5 = –120 + 95 = –25.
28. Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
28. Let A1, A2, A3, A4and A5 be five numbers between 8 and 26.
So, the A.P is 8, A1, A2, A3, A4, A5, 26. with n=7 terms.
Also, a = 8.
l=26, last term.
a+ (7 – 1)d=26
8+6d=26
6d=26 – 8
d=
d=3
So,
A1=a+d=8+3=11
A2=a+2d=8+2 × 3=8+6=14
A3=a+3d=8+3 × 3=8+9=17.
A4=a+9d=8+4 × 3=8+12=20
A5=a+5d=8+5 × 3=8+15=23.
Hence the reqd. five nos are 11,14,17,20 and 23.
33. Find the 20th and nth terms of the G.P.
33. Here, a=
=
so, an = arn-1
i.e a20=ar20-1=
and an= arn-1=
34. Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.
34. Given, r=2
Let a be the first term,
Then, a8= 92
ar8-1=192
a (2)7 = 192
a =
so, a =
a12 = ar12-1= (2)11 = 3 211-1
= 3×210
= 31024
= 3072.
Find the sum to indicated number of terms in each of the geometric progressions inExercises 39 to 42:
39. 0.15, 0.015, 0.0015, ... 20 terms.
39. Here a = 0.15 =
<1
n = 20
So, Sum to term of G.P.,
=
=
=
44. The sum of first three terms of a G.P. is and their product is 1. Find the common ratio and the terms.
44. Let the three terms of the G.P be
So,
=
=
And
= (as a = 1)
=
=
=
=
=
=
=
= or
= or
When the terms are,
When the terms are,
1, 1,
67. 3 × 12 + 5 × 22 + 7 × 32 + ...
67. The given series is 3 × 12 + 5 × 22 + 7 × 32 + …..
So,an = (nth term of A P 3, 5, 7, ..) (nth term of A P 1, 2, 3, ….)2
a = 3, d = 5 -3 = 2a = 1, d = 2 -1 = 1.
= [3 + (n- 1) 2] [1 + (n- 1) 1]2
=[3 + 2n- 2] [1 + n- 1]2
(2n + 1)(n)2
= 2n3 + n2
So, = 5n2∑n3 + ∑n2
Class 11 Sequence And Series Miscellaneous Exercise NCERT Solution
75. Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
75. Let a and d be the first term and common difference of the A.P.
So,
= 2 am
82. The sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
82. Given, a = 5
So,
Hence, last term
= 160
83. The first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.
83. Given, a = 1
Let r be the common ratio of the G.P.
So,
Let r be the common ratio of the G.P.
So,
Let so we can write above equation as
51. Find the sum of the products of the corresponding terms of the sequences 2, 4, 8,16, 32 and 128, 32, 8, 2, .
51. The sum of product of corresponding terms of the given
Sequences =
= 256+128+69+32+16
The above is a G.P. of a = 256, < 1 and x = 5
Sum required =
=
=
30. Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A. P. and the ratio of 7th and (m – 1)th numbers is 5 : 9. Find the value of m.
30. Let A1, A2, A3 . Am be the m terms such that,
1, A1, A2, A3, . Am, 31 is an A.P.
So, a=1, first term of A.P
n=m+2, no. of term of A.P
l=31, last term of A.P. or (m+2)th term.
a+ [ (m+2) –1]d =31
1 + [m+1]d =31
(m+1)d =31 – 1=30
d =
The ratio of 7th and (m – 1) number is
? a1term=a
a2 =A1=a+d
a3 =A2=a+2d
:
a8 = A7 = a + 7d
9 [a+7d]=5 [a+ (m – 1)d]
9a+63d=5a+5 (m – 1)d.
9a – 5a=5 (m – 1)d – 63d.
4a= [5 (m – 1) –63]d.
So, putting a=1 and d=
4 × 1= [5 (m – 1) –63] ×
4 (m+1)= [5 (m – 1) –63] × 30
4m+4= [5m – 5 – 63] × 30
4m+4 =150m – 68 × 30 => 150m – 2040
150m – 4m =2040+4
146m =2044.
m =
m =14.
50. Find the sum to n terms of the sequence, 8, 88, 888, 8888… .
50. The given sequence, 8, 88, 888, 8888, …., upto xterm is not a G.P. so we can such that it will be changed to a G.P. by the following .
Sum of x terms, sx = 8+ 88+888+8888 …..upto x term
= upto x term
Multiplying the numerator and denumerator by 9 we get,
= x terms
= upto x terms
= [(10 + 1010 + 103 +104 ……..upto, x terms) (1 +1 + 1 + 1 …… upto, x terms)]
=
=
=
61. If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are ![]()
61. Let a and b be the two number and a> b so a-b = (+ ve)
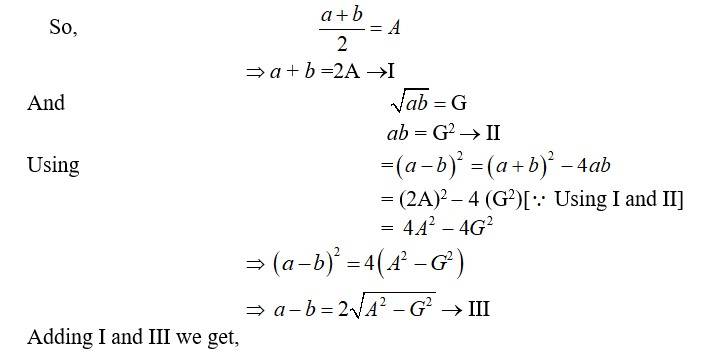
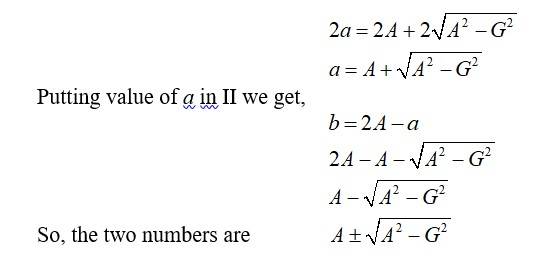
62. The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ?
62. Since the numbers of bacteria doubles every hour. The number after every hour will be a G.P
So, a=30
r=2
At end of 2nd hour, a3 (or 3rd term) =
= 30×24
= 120
At end of 4th hour, a5 (r 4th term) =
= 30×24
= 30×16
= 480
Following the trend,
And at the end of nth hour, an+1=
= 30 ×2n
Sequence And Series Exercise 8.1 Solutions
Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:
1. an = n (n + 2)
1. Here an = n (n + 2)
Substituting n=1,2,3,4,5 we get,
a1=1 (1+2)=1 * 3=3
a2=2 (2+2)=2 * 4=8
a3=3 (3+2)=3 * 5=15
a4=4 (4+2)=4 * 6=24
a5=5 (5+2)=5 * 7=35.
Hence, the first five terms are 3,8,15,24 and 35
5. an = (–1)n – 1 5n + 1
5. Here, an= (–1)n – 1 . 5n+1
Putting n=1,2,3,4,5 we get,
a1= (–1)1 – 1.51+1= (–1)0× 52=25
a2= (–1)2 – 1.52+1= (–1)1× 53= –125
a3= (–1)3 – 1. 53+1= (–1)2× 54=625
a4= (–1)4 – 1. 54+1= (–1)3. 55= –3125
a5= (–1)5 – 1. 55+1= (–1)4. 56=15625.
Hence, the first five terms are 25, –125,625, –3125 and 15625.
7. an = 4n – 3; a17, a24
7. an = 4n – 3.
Putting n = 17, we get
a17 = 4 * 17 – 3=68 – 3 = 65.
and putting n = 24 we get,
a24 = 4 * 24 – 3 = 96 – 3 = 93
8. ; a7
8.
Put n=7,
9. an = ( –1)n – 1n3; a9
9. an= ( –1)n – 1 .n3.
Put n=9 we get,
aq= (–1)9 – 1.93= (–1)8. 729=729.
10. ;a20
10. .
Put n=20,
Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:
11. a1= 3, an= 3an – 1+ 2 for all n > 1
11. Given, a1=3
an=3an – 1.+2 "n>1.
Putting n=2,3,4,5 we get,
a2=3a2 – 1+2=3a1+2=3 * 3+2=9+2=11
a3=3a3 – 1+2=3a2+2=3 * 11+2=33+2=35
a4=3a4 – 1+2=3a3+2=3 * 35+2=105+2=107.
a5=3a5 – 1+2=3a4+2=3 * 107+2=321+2=323.
Hence, the first five terms of the sequence are 3,11,35,107,323.
And the series is 3+11+35+107+323+ …
12. a1 = –1,
12. Given, a1= –1,
Putting n=2,3,4,5 we get,
.
So the first five terms of the sequence are –1, and .
And the series is .
13. a1 = a2= 2, an = an – 1–1, n > 2
13. Given,
a1=a2=2.
an=an – 1 – 1
Putting n=3,4,5.
a3=a3 – 1 – 1=a3 – 1 – 1=a2 – 1=2 – 1=1
a4=a4 – 1 – 1=a3 – 1=1 – 1=0
a5=a5 – 1 – 1=a4 – 1=0 – 1= –1 .
Hence the first five forms of the sequence are 2,2,1,0, –1.
And the series is 2+2+1+0+ (–1)+ ….
14. The Fibonacci sequence is defined by 1 = a1 = a2 and an= an – 1 + an – 2, n > 2. Find , for n = 1, 2, 3, 4, 5.
14. Given, a1=1=a2.
an=an – 1+an – 2,n>2.
We need to find,
Putting n=3,4,5,6 in an=an – 1+an – 2 we have,
a3=a3 – 1+a3 – 2=a2+a1=1+1=2.
a4=a4 – 1+a4 – 2=a3+a2=2+1=3.
a5=a5 – 1+a5 – 2=a4+a3=3+2=5.
a6=a6 – 1+a6 – 2=a5+a4=5+3=8.
Now, to find ,
Substitute n=1,2,3,4,5.
.
16. Find the sum of all natural numbers lying between 100 and 1000, which are multiples of 5.
16. Sum of all natural number between 100 and 1000 which are multiple of 5.
=105+110+115+ … +995.
So, a=105.
a=110 – 105=5.
As the last term is 995 which is the nthterm,
a+ (n – 1)d =995.
105+ (n – 1) × 5 =995.
(n – 1) × 5=995 – 105.
(n – 1)5 =890
n – 1 =
n =178+1
n =179
So, required sum Sn (a+l); l=last term.
= 179 × 550
=98450.
19. In an A.P., if pth term is and qth term is , prove that the sum of first pqterms is (pq+1), where p ≠ q.
19. Let a and d be the first term and the common difference of an A.P.
Then, given ap =
a+(p – 1)d = --------(1)
and aq =
a+(q – 1)d = ---------(2)
Subtracting eqn (2) from (1) we get,
a+(p – 1)d – [a+(q – 1)d]=
a+(p – 1)d– a–(q– 1)d=
[(p – 1)–(q – 1)]d=
[p – 1 – q+1]d=
[p – q]d= .
d= .
Putting d= in eqn (1) we get,
.
.
So, sum of first pq terms,
= .
=
20. If the sum of a certain number of terms of the A.P. 25, 22, 19, … is 116. Find the last term.
20. The given A.P. is 25,22,19, …
So, a=25
d=22 – 25= –3
Given that, sum of first n terms of the AP=116.
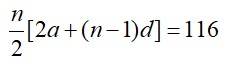
n [2 × 25+ (n – 1) (–3)]=116 × 2
n [50 – 3n+3]=232
n [53 – 3n]=232 .
53n – 3n2=232.
3n2 – 53n+232.
Using quadratic formula, a=3, b= –53, c=232.
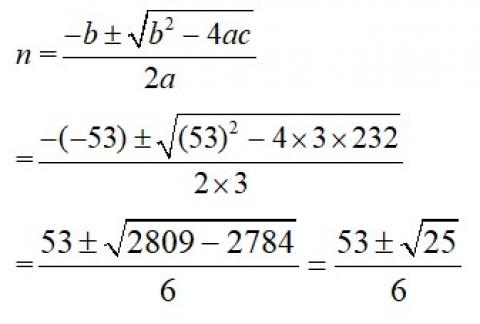
n = or
= or
= or 8.
As n N, n=8.
? Last term=a+ (n – 1)d
=a+ (8 – 1)d
=25+7× (–3)
=25 – 21
=4.
21. Find the sum to n terms of the A.P., whose kth term is 5k + 1.
21. Given, ak =5k+1
Putting k =1,
a1 =5 × 1+1=5+1=6.
an =5n+1=l
So, sum of unto n teams of the AP, Sn =
Sn =
= .
22. If the sum of n terms of an A.P. is (pn+ qn2), where p and q are constants,find the common difference.
22. Given, sum of n terms of A.P, Sn= (pn+qn2), p&q are constants substituting n=1,
S1=p× 1+q× 12=p+q=a1 [sum upto1st term only]
And substituting n=2,
S2=p× 2+q× 22=2p+4q=a1+q2 [sum upto 2ndtern only]
So, a1+a2=2p+4q
⇒ a2=2p+4q – a1=2p+4q – (p+q)=2p – p+4q – q
⇒ a2=p+3q
So, common difference, d=a2 – a1
= (p+3q) – (p+q)
=p+3q – p – q
=2q.
23. The sums of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 18th terms.
23. Let a1, a2 be the first terms and d1, d2 be the common difference of the first term A.P.S
So,
---------------(1)
The ratio of their 18thterms.
=
=
= --------(2)
Comparing eqn (1) and (2),
=
So, ratio of their 18th terms =
24. If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.
24. Let a and d be the first elements and common different of the A.P.
Then, Sum of first p terms of the AP=Sum of first q terms of A.P
Sp=Sq
p [2a+pd – d]=q [2a+qd – d]
2ap+p2d – pd=2aq+q2d – qd
2ap – 2aq+p2d – q2d – pd+qd=0
2a (p – q)+ [p2 – q2 – p+q]d=0.
2a (p – q)+ [ (p – q) (p+q) – (p – q)]d=0
(p – q) {2a+ [ (p+q) – 1]d}=0
Deviding both sides by p – q,
2a+ [ (p+q) –1]d=0.
And multiplying by P+Q/2 we get,
which in the form where n=p+q.
Sp+q=0.
25. Sum of the first p, q and r terms of an A.P. are a, b and c, respectively. Prove that + = 0
25. Let e and d the first term and common difference of an AP.
Then,
Sum of first p terms, Sp=a.
.
Similarly, Sq=b
----------------(2)
And. Sr=C
-----------------(3)
So, L.H.S. + (? given)
= + +
= + +
=c[q – r+r – p+p – q]+ [(p – 1)(q – r)+(q – 1)(r – p)+(r – 1)(p – q)]
=C × 0 + [pq – pr – q+r+qr – pq – r+p+pr=qr – p+q]
=0+ [pq – pq – pr+pr – q+q+r – r+qr+qr+p – p]
=
=0.
=R.H.S.
26. The ratio of the sums of m and nterms of an A.P. is m2 :n2. Show that the ratioof mthand nth term is (2m – 1) : (2n – 1).
26. Let a and d be the first term and common difference of A.P.
Then,
Dividing both sides by m/n we get,
[2a+(n – 1)d]n=m[2a+(n – 1)d].
2an+dmn – dn=2am+dmn – dm.
2an – 2am=dn – dm+2mn – dmn
2a(n – m)=d(n – m)
d=
d=2a.
Now, Ratio of mth and nthterm
=
Putting d=2a in the above we get,
ratio of mth and nth term =
=
=
=
= .
27. If the sum of n terms of an A.P. is 3n2 + 5n and its mth term is 164, find the value of m.
27. Given,
Sum of n terms of AP, Sn=3n2+5n
Put n=1,
S1=3 × 12+5 × 1=3+5=8=a1 (? S1=sum of 1* terms of AP)
Put n=2,
S2=3 × 22+5 × 2=3 × 4+10=12+10 =22
=a1+a2 (? Sum of first two term of A.P)
So, a1+a2=22
8 +a2=22
a2=22 – 8
a2=14
? First term, a=a1=8
Common difference, d=a2 – a1=14 – 8=6
Now, given that, am = 164.
a+ (m – 1)d=164.
8+ (m – 1)6=164.
(m – 1)6=164 – 8.
m – 1=
m=26+1
m=27.
29. If is the A.M. between a and b, then find the value of n.
29. Given,
A.M between a and b=
And
2 [an+bn]= (a+b) (an – 1+bn – 1)
2an+2bn=an – 1.a+abn – 1+ban – 1 + bn – 1.b
2an+2bn=an – 1 + 1+ abn – 1+ban – 1 + bn – 1 + 1
2an+2bn=an+ abn – 1+bn – 1 + bn
2an – an – ban – 1 = abn – 1 + bn– 2bn
an – ban – 1=abn – 1 – bn
an – 1 [a – b]=bn – 1 [a – b] [? an=an – 1+1=an – 1 .a1]
an – 1=bn – 1.
.
[? a0=1].
n – 1=0
n=1.
31. A man starts repaying a loan as first instalment of Rs. 100. If he increases the instalment by Rs 5 every month, what amount he will pay in the 30th instalment?
31. Since the man starts paying installmentas? 100 and increases? 5 every month.
a=100
d=5.
So, the A.P is 100,105,110,115, ….
? Amount of 30thinstallment=30th term of A.P =a30
=a+ (30 – 1)d
=100+29 × 5.
=100+145
= ?245
i.e., He will pay? 245 in his 30th instalment.
36. The 4th term of a G.P. is square of its second term, and the first term is – 3.Determine its 7th term.
36. Given, a = 3
Let r be the common ratio of the G.P.
Then, a4 = (a2)2
ar4-1 = (ar2-1)2
ar3= (ar)2
ar3= a2r2
r = a = 3
a7 = ar7-1 = ar6= (-3) (-3)6 = (-3)7 = -2187.
38. For what values of x, the numbers , , are in G.P.?
38. For , , to be in G.P. we have the condition,
41. 1, – a, a2, – a3, ... n terms (if a ¹ – 1).
41. Here,
So,
=
=
43. Evaluate
43.
[2+2+ ….+ (11lines)] + (31+ 32+……+311)
=
=
45. How many terms of G.P. 3, 32, 33, … are needed to give the sum 120?
45. Given, a=3
>1
If sn=120
Then
3n= 80+1
3n= 81
= 3n = 34
So, 120 is the sum of first 4 terms of the G.P
46. The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
46. Let a be the first term and r be the common ratio of the G.P.
Then
………. I
Also
…… II
Dividing II and I we get,
r3= 8
r3 = 23
r = 2 >1
So, putting r = 2 in I we get,
And
47. Given a G.P. with a = 729 and 7th term 64, determine S7.
47. Given, a= 729
729. r6 = 64
<1
When
=
=
=
= 2059
When
=
=
= 463
48. Find a G.P. for which sum of the first two terms is – 4 and the fifth term is 4 times the third term.
48. Let a and r be the first term and common ratio.
Then,
a (1+ n) = 4
r2 = 4
r2 =22
r = ±2
When r =2
a (1+2)=-4
a 3 = -4
So, the G.P. is a, ar, ar2,………….
When
a = (-) = -4
a = 4
So, the reqd. by G.P. is a, ar, ar2…………. 4, 4 (-2), 4 (-2)2, .................
4, 8, 16, ..........
49. If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P.
49. Let aand r be the first term and common ration of the G.P.
So,
- I
And a10 = y
- II
Also a 16 = z
- III
So,
and
x, y, z are in G.P
52. Show that the products of the corresponding terms of the sequences a, ar, ar2,…arn– 1 and A, AR, AR2,…ARn – 1 form a G.P, and find the common ratio.
The product of corresponding terms of the given sequence are
=
=
So, looking at the sequence forms a G.P.
(above the)
With common ratio =
53. Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
53. Let the four numbers is G.P. be a, ar, ar2, ar3
Given,
I
And
II
Dividing II by I we get,
r = 2
So, putting r = 2 in I we get ,
a = 3
The four numbers are 3, 3´(-2), 3´(-2)2, 3´(-2)3
3, 6, 12, 24
54. If the pth, qth and rth terms of a G.P. are a, b and c, respectively. Prove that aq – rbr – pcP – q= 1
54. Let a and r be the first term and common ratio of the G.P.
Then, ap = a
…… I
and aq = b
…….II
Also, ar = c
…..III
Given, L.H.S. =
using I, II and III
A0 R[pqprq+r+qrpqr+p+prqrp+q]
= R
= 1
= R.H.S
55. If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
55. Given, first term and xth term and a and b
Let r be the common ratio of the G.P.
Then,
Product of x terms, p= ……
p= ….
= (a ×a× ….n term)(r´r2´r3 ….. )
=
p =
So, [We know that,
= [
= [So,
=
= last term = b (given)]
=
56. Show that the ratio of the sum of first nterms of a G.P. to the sum of terms from(n + 1)th to (2n)th term is
56. Let a and r be the first term and common difference of the G.P
Thus, Sum of the first on term,
Let Sn = sum of term from (n+1)th to (2n)th term
=
=
[ the above is a G.P. with first term arx and common ratio =
and number of term from (2n)th to (n+1)th = n
So,
=
=
57. If a, b, c and d are in G.P. show that (a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc+ cd)2 .
57. Let r be the common ratio of the G.P. then,
First term = a1 = a = a
So, L.H.S.=
=
=
=
=
R.H.S.=
=
=
= { }
=
L.H.S. = R.H.S.
58. Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
58. Let G1 and G2 be the two numbers between 3 and 81 so that 3, G1, G2, 81 is in G.P.
So, a = 3
a4 = ar3 = 81 (when r = common ratio)
r3 = 27
r3 = 33
r = 3
So, G1 = ar = 33=9 and G2 = ar2 3´ (3)2 =27
59. Find the value of n so that may be the geometric mean between a and b.
59. We know that,
G.M between a and b = √ab
Given
60. The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio (3 + 2√2) : (3 - 2√2).
60. Let a and b be the two numbers and a>b so a-b = (+ ve)
So, sum of two numbers = 6. G.M of a and b

Class 11 Math Sequence And Series Ex 8.4 Solutions
Find the sum to n terms of each of the series in Exercises 65 to 71.
65. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 +...
65. Given series is 1×2+2 ×3+3× 4+4× 5+…
So, an (nth term of A.P 1, 2, 3…) (nth term of A.P. 2, 3, 4, 5…)
i e, a = 2, d = 2 -1 = 1i e, a = 2, d = 3 - 2 = 1
= [1 + (n- 1) 1] [2 + (n -1) 1]
= [1 + n- 1] [2 + n -1]
= n (n -1)
= n2-n.
Sn (sum of n terms of the series) = ∑n2 + ∑n.
Sn = +
=
=
66. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + ...
66. Given series is 1× 2× 3 + 2× 3 ×4 + 3× 4 ×5 + … to n term
an = (nth term of A. P. 1, 2, 3, …) ´× (nth terms of A. P. 2, 3, 4) ×
i e, a = 1, d = 2- 1 = 1i e, a = 2, d = 3- 2 = 1
(nth term of A. P. 3, 4, 5)
i e, a = 3, d = 3 -4 = 1.
= [1 + (n -1) 1] ×[2 + (n -1):1]× [3 + (n- 1) 1]
= (1 + n -1)×(2 + n -1)×(3 + n -1)
= n (n + 1)(n + 2)
= n(n2 + 2n + n + 2)
=n3 + 2n2 + 2n.
Sn = ∑n3 + 3 ∑n2 + 2 ∑n
=
=
68.
68. The given series is
So, an =
So. Putting n = 1, 2, 3….n.
a1 =
a2 =
a3 =
So, adding. L.H.S and R.H.S. up ton terms
a1 + a2 + a3 + … + an =
Sn = 1 { equal terns cancelled out}
Sn =
Sn =
69. 52 + 62 + 72 + ... + 202
69. The given series is 52 + 62 + 72 + … + 202
This can be rewritten as (12 +22 + 32 + 42 + 52 + 62 + 72 + … + 202) - (12 + 22 + 32 + 42)
So, sum = (12 + 22 + 32 + 42 … + 202) - (12 + 22+ 32 + 42)
= 2870 30
= 2840.
70. 3 × 8 + 6 × 11 + 9 × 14 + ...
70. The given series is 3 8 + 11 + 9 14 + …
So, an= (nth term of 3, 6, 9, …) (nth term of 8, 11, 14, …)
i e, a = 3, d = 6- 3 = 3i e, a= 8, d = 11- 8 = 3
= [3 + (n- 1) 3] [8 + (n -1) 3]
= [3 + 3n- 3] [8 + 3n -3]
= 3n (3n + 5)
= 9n2 + 15n.
So, Sn = 9∑n2 + 15∑ n.
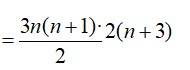
= 3n (n + 1) (n + 3)
71. 12 + (12 + 22) + (12 + 22 + 32) + ...
71. The given series is 12 + (12 + 22) + (12 + 22 + 32) + …
So, nth term well be
an =12 + 22 + 32 + … + n2.
So, Sn =
Find the sum to n terms of the series in Exercises 72 to 74 whose nth terms is given by
72. n(n+1) (n+4).
72. Given that,
an = n(n + 1)(n + 4)
= n(n2 + 4n + n + 4)
=n(n2 + 5n + 4)
= x3 + 5x2 + 4x
So, sum of terms, Sn =
76. If the sum of three numbers in A.P., is 24 and their product is 440, find the numbers.
76. Let the three numbers a d, a, a + d be in A.P.
Then,
3a = 24
a = 8
and,
Put,
When d = 3, a = 8 the three number are.
8 3, 8, 8 + 3 5,8,11
When d = 3, a = 8 the three numbers are.
77. Let the sum of n, 2n, 3n terms of an A.P. be S1, S2 and S3, respectively, show that S3 = 3(S2 – S1)
77. Let a and d be the first term and common difference of an A.P.
Then,
Now, R.H.S
78. The smallest and largest no. between 200 and 400 which are divisible by 7 is
78.
So we can form an A.P. 203,203+7, …..., 399-7, 399
So, i.e. a = 203 and d = 7
l = 399
Sum of the 29 number of the AP = Required sum =
= 8729.
79. Find the sum of integers from 1 to 100 that are divisible by 2 or 5.
79. An A.P. of numbers from 1 to 100 divisible by 2 is
2, 4, 6, ……….98, 100.
So, a = 2 and d = 4-2 = 2
100
Let,
= 2550
Similarly, an A.P. of numbers from 1 to 100 divisible by 5 is
5,10,15, …….. 95,100
So, a = 5 and d = 100
100
= 1050
As there are also no divisible by both 2 and 5 , i.e., LCM of 2 and 5 = 10 An A.P. of no. from 1 to 100 divisible by 10 is 10, 20, …………100
So, a = 10, d = 10
So,
= 550
The required sum of number
= 3050
80. Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder
80. Two digits no. when divided by 4 yields 1 as remainder are, 12+1, 16+1, 20+1 …., 96+1
13, 17, 21, ………97 which forms an A.P.
So, a = 13
Sum of numbers in A.P. =
= 11× 110
= 1210
81. If f is a function satisfying f (x +y) = f(x) f(y) for all x, y N such that f(1) = 3 and , find the value of n.
81. Given, and
Putting (x, y) = (1+1) we get
Putting (x, y) = (1,1) we get,
And putting we get,
(Given)
As, With a = 3
We can write equation I as ,
3n 1 = 80
3n = 81 +1
3n = 81
3n = 34
n = 4
84. The sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.
84. Let a, ar and be the three nos. which is in G.P.
Then, a + ar + ar2 = 56
a ( 1 + r + r2) =56 -I
Given, that a1, ar 7, ar2 - 21 from an AP we have,
………………. II
Now, dividing equation I by II we get,
(dividing by 3 throughout)
So, when r = 2, putting in equation I,
The numbers are 8, 8× 2, 8× 22 = 8, 16, 32.
And When putting in equation I,
So, the numbers are
85. A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
85. Let a and r be the first term and common ratio of G.P.
Then, number of term = 2n (even).
{ series on R.H.S. has terms and common ratio }
(eliminating a)
r = 4
86. The sum of the first four terms of an A.P. is 56. The sum of the last four terms is 112. If its first term is 11, then find the number of terms.
86. Given, a = 11
Let d and l be the common difference & last term of the A.P.
Then, [first 4 terms sum]
And,
[last 4 terms sum]
So,
the A.P. has 11 number of terms.
87. If ( x ≠ 0) , then show that a, b, c and d are in G.P.
87. Here,
…………I
And
……………II
From I and II
a, b, c and d are in G.P.
88. Let S be the sum, P the product and R the sum of reciprocals of n terms in a G.P. Prove that P2Rn = Sn.
88. Let a and r be the first term & common ratio of the G.P.
So, S = a +ar + ar2 +……… upto n terms.
and P = a .ar. ar2 ar .... upton n terms.
And R = sum of reciprocal of n terms ( upto n terms)
As r <1
>1
…. III
Now, L.H.S. = P2 Rn
{ equation II & III}
R.H.S { equation I}
89. The pth, qth and rth te.rms of an A.P. are a, b, c, respectively. Show that (q – r )a + (r – p )b + (p – q )c = 0
89. Let A and d be the first term & common difference of the A.P.
Then,
………I

…………III
So, L.H.S.
{putting value for I, II, III}
R.H.S
90. If are in A.P., prove that a, b, c are in A.P
90. Given, are in A.P.
So, are in A.P.
are in A.P.
If we add 1 to all each terms of the sequence it will given be an A.P of common difference 1.
So, are in A.P.
are in A.P.
Dividing add of the sum by ab + bc + ac will conserve.
then A.P so,
are in A.P.
Similarly multiplying each term by abc we get,
are in A.P.
a, b, c, are in A.P.
Hence proved
91. If a, b, c, d are in G.P, prove that (an + bn), (bn + cn), (cn + dn) are in G.P.
91. Let r be the common ratio of the G.P.
Then, a, b, c, d a, ar, ar2, ar3
So,
(2)
(3)
Hence, {from (2) and (1)}
and {from (3) and (2)}
i.e.,
are in A.P
92. If a and b are the roots of x2 – 3x + p = 0 and c, d are roots of x2 – 12x + q = 0, where a, b, c, d form a G.P. Prove that (q + p) : (q – p) = 17:15.
92. Given, ab are roots of
and c & d are roots of
So, and
a + b = +3 …………..I and ab = P…………….II { sum of roots = , Product of roots = }
Similarly, c + d and
c + d = 12 ……….III ad cd = q (4)
As a, b, c, d from a G.P and if r be the common ratio
a = a
b = ar
c = ar2
d = ar3
So, from equation, (1),
(5)
And (6)
Dividing equation (6) and (5) we get,
r2 = 4
Now, L.H.S. {from (4) and (5)}
= R.H.S.
94. If a, b, c are in A.P.; b, c, d are in G.P. and are in A.P. prove that a, c, e are in G.P.
94. As a, b, c are in A.P. we can write,
I
As b, c, d are in G.P. we can write,
II
And ar are in A.P. we can write,
…………. III
Now, from II
{from 1 and 3}
i.e., a, c and e are in G.P.
95. Find the sum of the following series up to n terms:
(i) 5 + 55 +555 + …
(ii) .6 +. 66 +. 666+…
95. (i) Sn = 5+55+555+…………… upto n term
=5(1+11+111+ …………….upto n term )
Multiplying and dividing by 9 we get
(ii)
96. Find the 20th term of the series 2 × 4 + 4 × 6 + 6 × 8 + ... + n terms.
96. Given, series is
So, a20 = ( 20th term of A.P. 2, 4, 6 ….) ( 20th term of A.P. 4,6,8 ………)
i.e. a = 2, d = 4 -2 = 2 i.e. a =4, d = 6- 4 = 2
= [2 + (20- 1)2] [4 + (20-1)2]
= [2+19*2] [4 +19 *2]
= (2+38) (4+38)
= 40*42 = 1680
97. Find the sum of the first n terms of the series: 3+ 7 +13 +21 +31 +…
97. The given series is 3+7+13+21+31+ …….. upto n terms
So, Sum, Sn = 3+7+13+21+31+ ………….+ an-1 + an
Now, taking,
Sn = Sn = [ 3 + 7 + 13 + 21 + 31 + ………. an-1 + an ] [ 3+ 7 + 21 + 31 + … an-1 + an]
0 = [ 3+ (7 - 3) + (13 - 7) + (13 - 7) + (21 - 13) + …….+ (an an-1) - an]
0 = 3 + [ 4 + 6 + 8 +……..+ (n-1) terms] an
an = 3 + n2 + (1 + 2) n + (-1) (2) {
an = 3 + n2 + n- 2 = n2 + n +1
sum of series,
98. If S1, S2, S3 are the sum of first n natural numbers, their squares and their cubes, respectively, show that 9 S22 = S3 (1 + 8S1).
98. Given,
S1 = 1 + 2 + 3 + ………. + n
S2 = 12 + 22 + 32 + ………… + n2
S3 = 13 + 23 + 33 + …………. + n3 =
So, L.H.S.
R.H.S.
So, 9(S2)2 = S3 ( 1 + 8S1)
99. Find the sum of the following series up to n terms:
99. The given series is.
The nth term is ,
100. Show that
100. Given,
For numerator,
a (nth term) = n (n + 1)2 = n (n + 1)2 = n (n2 + 2n +1) = n3 + 2n2 + n
So,
For denominator,
an (nth term) = n2 (n + 1) = n3 + n2
So,
So,
101. A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to pay the balance in annual instalments of Rs 500 plus 12% interest on the unpaid amount. How much will the tractor cost him?
101. Given,
cost of tractor =? 12,000
Amount paid =? 62,000
Amount unpaid =? 12000 -? 6000 =? 6000
So, number of instalments =
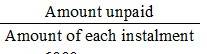
= 12 = n
Now, interest on 1st installment = interest on unpaid amount ( i.e.? 6000) for 1 Year.
=?
Similarly,
Interest on 2nd installment = interest on (? 6000 -? 500) for the next 1 year
=?
And,
Interest on 2nd installment =?
=? 600
Here, Total (interest per) installment paid =? (720 + 660 + 600 + ……. upto 12 terms)
= 6 [ 1440 - 660]
= 6 × 780
=? 4680
So, the total cost of tractor = cost price + installments
=? 12,000 +? 4680
=? 16680
102. Shamshad Ali buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in annual instalment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?
102. Given, cost of scooter = ?22,000
Amount paid =? 4000
Amount unpaid =? 22,000 -? 4000 =? 18,000
Now, Number of installments =Amount unpaid/Amount of each instalment
As he per 10% interest on up unpaid amount and ?1000 each installment
Amount of 1st instalment =? 1000 +?
Amount of 2nd installment =? 1000 +?
Similarly,
Amount of 3rd installment =? 1000 +?
So, Total installment paid =? 2800 +? 1600 =? 2600 + …… upto 18 installment
= 9 [5600 - 1700]
= 9 × 3900
=? 35,000
Total cost of scooter = Amount + Total installment paid
=? 4000 +? 35,100
=? 39100
103. A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.
103. As the number of letters mailed forms a G.P. i.e., 4, 42, ……., 48
We have,
a = 4
and n = 8
So, Total numbers of letters = 4 + 43 + ……. + 48
= 87380
As amount spent on one postage = 50 paise
So, for reqd. postage =?
=? 43690
104. A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 15th year since he deposited the amount and also calculate the total amount after 20 years.
104. Given,
Principal amount =? 10000
Amount at end of 1 year =?
=? (10000 + 500)
=? 10500 {Amount paid = principal + S.I. in a year}
Amount at end of 2nd year
=?
=? (10000 + 1000)10500 + 500
=? 11000
Amount at end of 3rd year
=?
=? (1000 + 1500)
=? 11500
So, amount at end of 1st, 2nd, 3rd ………, nth year forms as A.P.
i.e.? 10500? 11000? 115000, ………. with
a = 10500
d = 11000 - 10500 = 500
Now, Amount in 15th year = Amount at end of 14th year
=? 10500 + ( 14 - 1) × 500
=? 10500 + 13 × 500
=? 10500 + 6500
=? 17000
Similarly amount after 20th year, =? 10500+ (20 - 1) × 500
=? 10500 + 19 × 500
=? 10500 + 9500
=? 20,000
105. A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.
105. Given,
Cost of machine =? 15625
depreciation rate = 20 % each year.
We have,
Depreciated value after 1st year =? 15625 - 20 % of 15625
=?
=?
=?
=?
Similarly,
Depreciated value after 2nd year =? 15625
This, Depreciated value at end of 5 years
=? 15625
=? 15625
=? 5120
106. 150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
106. Let ‘x’ be the no of days in which 150 workers took to finish the job.
If 150 workers worked for x days then number of workers for x days =150 x.
But given that number of works dropped 4 on 2nd day, then 4 on 3rd day and so on taking 8 more
days to finish the work. i.e., x + 8 days we can express as.
150 x = 150 + (150
150 x = 150 + 146 + 142 +……… (x+8) days which
R.H.S. from as A.P. of
a = 150
d = -4 and n = x +8
So, Sn = 150 x
n [ 150 + (n - 1) (-2)] = 150 (n - 8) [
150n 2n (n - 1) 150n 1200
2n2 + 2n 1200 =0
n2 - n - 600 = 0 [ dividing by -2 throughout]
n2 - 25 n + 24 n 600 = 0
n (n - 25) + 24 (n - 25) = 0
(n - 25) (n + 24) = 0
n = 25 or n = -24 (which is not possible)
So, n = 25 days
i.e. x + 8 = 25 days
2. Kindly Consider the following an=
2. Here, a1=
Substituting n=1,2,3,4,5 we get,
Hence the first five terns are
3. Kindly Consider the following an=2n
3. Here an=2n
Substituting n=1,2,3,4,5 we get,
a1=21=2
a2=22=4
a3=23=8
a4=a4=16
a5=25=32.
Hence the first five terns are 2,4,16,32 and 64.
6. Kindly Consider the following an = n
6. Here, an=n
Putting n=1,2,3,4,5 we get,
Hence, the first five terms are
Class 11 Math Sequence And Series Exercise 8.2 Solutions
Ex 8.2 Class 11 Math covers geometric progression (GP), an essential type of sequence where each term is obtained by multiplying the previous term by a fixed ratio. class 11 Sequence and Series exercise 8.2 focuses on concepts such as the nth term of a GP, the sum of n terms, and sum of an infinite GP, which are important to finding exponential growth and decay. Students can check the solution of 18 questions of exercise 8.2 below;
Class 11 Sequence And Series Exercise 8.2 SolutionQ1. Find the sum of odd integers from 1 to 2001. |
| A.1. Sum of odd integers from 1 to 2001 =1+3+5+ … +2001 So, a=1 d=3 – 1=2 ⸫ For nth term, an=a+(n – 1)d. ⸪ the last nth term is 2001, 2001 =1+(n – 1)2. (n – 1)2 =2001 – 1 n – 1=
n =1000+1 n =1001. ⸫ Sum of n terms, Sn=
⸫ Required sum =
|
| Q2. Find the sum of all natural numbers lying between 100 and 1000, which aremultiples of 5. |
| A.2. Sum of all natural number between 100 and 1000 which are multiple of 5. =105+110+115+ … +995. So,a=105. a=110 – 105=5. As the last term is 995 which is the nthterm, a+(n – 1)d =995. 105+(n – 1) × 5 =995. (n – 1) × 5=995 – 105. (n – 1)5 =890 n – 1 =
n =178+1 n =179 So, required sum Sn
= 179 × 550 =98450. |
| Q3. In an A.P., the first term is 2 and the sum of the first five terms is one-fourth ofthe next five terms. Show that 20thterm is –112. |
| A.3. Given, a=2 Let A1, A2, A3, A4, A5, A6, A1, A6, A7, A10 be the first ten terms. So, A1=a. Given A1+A2+A3+A4+A5=
a+(a+d)+(a+2d)+(a+3d)+(a+4d) =
5a+10d=
4[5a+10d]=9a+35d. 20a+40d=5a+35d. 40d – 35d=5a – 20a 5d= –15a d= –3a d= –3 × 2 [as a=2] d= –6 So, A20=a+(20 – 1)d =2+19 × (–6) =2 – 114 = –112. |
| Q4. How many terms of the A.P. – 6,
|
| A.4. Let the sum of n farms of the A.P –6,
Then,
From the given A.P. a= –6 d= –
So, –25=
–25 × 2=n
–50=n
–50=n
–50 × 2 =n[n – 25]=n2 – 25n n2 – 25n+100=0. n2 – 5n – 20n+100=0 n(n – 5) – 20(n – 5)=0 (n – 5)(n – 20)=0 So, n=5 and n=20. When n=5
When n=20
|
| Q5. In an A.P., if pth term is
|
| A.5. Let a and d be the first term and the common difference of an A.P. Then, given ap =
a+(p – 1)d =
and aq =
a+(q – 1)d =
Subtracting eqn (2) from (1) we get, a+(p – 1)d – [a+(q – 1)d]=
a+(p – 1)d– a–(q– 1)d=
[(p – 1)–(q – 1)]d=
[p – 1 – q+1]d=
[p – q]d=
d=
Putting d=
So, sum of first pq terms,
=
=
|
| Q6. If the sum of a certain number of terms of the A.P. 25, 22, 19, … is 116. Find thelast term. |
| A.6. The given A.P. is 25,22,19, … So,a=25 d=22 – 25= –3 Given that, sum of first n terms of the AP=116. n[2 × 25+(n – 1)(–3)]=116 × 2 n[50 – 3n+3]=232 n[53 – 3n]=232 . 53n – 3n2=232. 3n2 – 53n+232. Using quadratic formula, a=3, b= –53, c=232. n =
=
=
As n
⸫ Last term=a+(n – 1)d =a+(8 – 1)d =25+7×(–3) =25 – 21 =4. |
| Q7. Find the sum to n terms of the A.P., whose kthterm is 5k + 1. |
| A.7. Given,ak =5k+1 Putting k =1, a1 =5 × 1+1=5+1=6. an =5n+1=l So, sum of unto n teams of the AP,Sn =
Sn =
=
|
| Q8. If the sum of n terms of an A.P. is (pn+ qn2), where p and q are constants,find the common difference. |
| A.8. Given, sum of n terms of A.P, Sn=(pn+qn2), p&q are constants substituting n=1, S1=p× 1+q× 12=p+q=a1 [sum upto1st term only] And substituting n=2, S2=p× 2+q× 22=2p+4q=a1+q2 [sum upto 2ndtern only] So, a1+a2=2p+4q ⇒ a2=2p+4q – a1=2p+4q – (p+q)=2p – p+4q – q ⇒ a2=p+3q So, common difference, d=a2 – a1 =(p+3q) – (p+q) =p+3q – p – q =2q. |
| Q9. The sums of n terms of two arithmetic progressions are in the ratio5n + 4 : 9n + 6. Find the ratio of their 18th terms. |
| A.9. Let a1, a2 be the first terms and d1, d2 be the common difference of the first term A.P.S So,
The ratio of their 18thterms.
=
=
=
Comparing eqn (1) and (2),
So, ratio of their 18th terms =
|
| Q10. If the sum of first p terms of an A.P. is equal to the sum of the first q terms, thenfind the sum of the first (p + q) terms. |
| A.10. Let a and d be the first elements and common different of the A.P. Then, Sum of first p terms of the AP=Sum of first q terms of A.P Sp=Sq
p[2a+pd – d]=q[2a+qd – d] 2ap+p2d – pd=2aq+q2d – qd 2ap – 2aq+p2d – q2d – pd+qd=0 2a(p – q)+[p2 – q2 – p+q]d=0. 2a(p – q)+[(p – q)(p+q) – (p – q)]d=0 (p – q){2a+[(p+q) – 1]d}=0 Deviding both sides by p – q, 2a+[(p+q) –1]d=0. And multiplying by P+Q/2 we get,
Sp+q=0. |
| Q11. Sum of the first p, q and r terms of an A.P. are a, b and c, respectively. Prove that
|
| A.11. Let e and d the first term and common difference of an AP. Then, Sum of first p terms, Sp=a.
Similarly, Sq=b
And. Sr=C
So, L.H.S.
=
=
=c[q – r+r – p+p – q]+
=C × 0 +
=0+
=
=0. =R.H.S. |
| Q12. The ratio of the sums of m and nterms of an A.P. is m2 :n2. Show that the ratioof mthand nth term is (2m – 1) : (2n – 1). |
| A.12. Let a and d be the first term and common difference of A.P. Then,
Dividing both sides by m/n we get,
[2a+(n – 1)d]n=m[2a+(n – 1)d]. 2an+dmn – dn=2am+dmn – dm. 2an – 2am=dn – dm+2mn – dmn 2a(n – m)=d(n – m) d=
d=2a. Now, Ratio of mth and nthterm =
Putting d=2a in the above we get, ratio of mth and nth term =
=
=
=
=
|
| Q13. If the sum of n terms of an A.P. is 3n2 + 5n and its mth term is 164, find the valueof m. |
| A.13. Given, Sum of n terms of AP, Sn=3n2+5n Put n=1, S1=3 × 12+5 × 1=3+5=8=a1 (⸪ S1=sum of 1* terms of AP) Put n=2, S2=3 × 22+5 × 2=3 × 4+10=12+10 =22 =a1+a2(⸪ Sum of first two term of A.P) So, a1+a2=22 8 +a2=22 a2=22 – 8 a2=14 ⸫ First term, a=a1=8 Common difference, d=a2 – a1=14 – 8=6 Now, given that,am = 164. a+(m – 1)d=164. 8+(m – 1)6=164. (m – 1)6=164 – 8. m – 1=
m=26+1 m=27. |
| Q14. Insert five numbers between 8 and 26 such that the resulting sequence is an A.P. |
| A.14. Let A1, A2, A3, A4and A5 be five numbers between 8 and 26. So, the A.P is 8, A1, A2, A3, A4, A5, 26. with n=7 terms. Also,a = 8. l=26, last term. a+(7 – 1)d=26 8+6d=26 6d=26 – 8 d=
d=3 So, A1=a+d=8+3=11 A2=a+2d=8+2 × 3=8+6=14 A3=a+3d=8+3 × 3=8+9=17. A4=a+9d=8+4 × 3=8+12=20 A5=a+5d=8+5 × 3=8+15=23. Hence the reqd. five nos are 11,14,17,20 and 23. |
| Q15. If
|
| A.15. Given, A.M betwna and b=
And
2[an+bn]=(a+b)(an – 1+bn – 1) 2an+2bn=an – 1.a+abn – 1+ban – 1 + bn – 1.b 2an+2bn=an – 1 + 1+ abn – 1+ban – 1 + bn – 1 + 1 2an+2bn=an+ abn – 1+bn – 1 + bn 2an – an – ban – 1 = abn – 1 + bn– 2bn an – ban – 1=abn – 1 – bn an – 1[a – b]=bn – 1[a – b] [⸪ an=an – 1+1=an – 1 .a1] an – 1=bn – 1.
n – 1=0 n=1. |
| Q16. Between 1 and 31, m numbers have been inserted in such a way that the resultingsequence is an A. P. and the ratio of 7th and (m – 1)th numbers is 5 : 9. Find thevalue of m. |
| A.16. Let A1, A2, A3 ... Am be the m terms such that, 1, A1, A2, A3, ... Am, 31 is an A.P. So, a=1, first term of A.P n=m+2, no. of term of A.P l=31, last term of A.P. or (m+2)th term. a+[(m+2) –1]d =31 1 +[m+1]d =31 (m+1)d =31 – 1=30 d =
The ratio of 7th and (m – 1) number is
a2 =A1=a+d a3 =A2=a+2d : a8 = A7 = a + 7d 9[a+7d]=5[a+(m – 1)d] 9a+63d=5a+5(m – 1)d. 9a – 5a=5(m – 1)d – 63d. 4a=[5(m – 1) –63]d. So, putting a=1 and d=
4 × 1=[5(m – 1) –63] ×
4(m+1)=[5(m – 1) –63] × 30 4m+4=[5m – 5 – 63] × 30 4m+4 =150m – 68 × 30 => 150m – 2040 150m – 4m =2040+4 146m =2044. m =
m =14. |
| Q17. A man starts repaying a loan as first instalment of Rs. 100. If he increases the instalment by Rs 5 every month, what amount he will pay in the 30th instalment? |
| A.17. Since the man starts paying installmentas ₹ 100 and increases ₹ 5 every month. a=100 d=5. So, the A.P is 100,105,110,115, …. ⸫Amount of 30thinstallment=30th term of A.P =a30 =a+(30 – 1)d =100+29 × 5. =100+145 = ₹245 i.e., He will pay ₹ 245 in his 30th instalment. |
| Q18. The difference between any two consecutive interior angles of a polygon is 5°.If the smallest angle is 120° , find the number of the sides of the polygon. |
| A.18. Let 'n' be the no. of sides of a polygon. So, sum of all angles of a polygon with sides n =(2n – 4) × 90° =(n – 2) × 2 × 90° =(n – 2)180° As the smallest angle is 120° and the difference between 2 consecutive interior angle is 5°. We have, a =120° d =5° So, sum of n sides =180°(n – 2).
n[240°+5°n – 5°]=360°n– 720° n[5°n+235°]=360°n – 720° 5°n2+235°n=360°n – 720° n2+47°n=72n – 144 [⸪ dividing by 5] n2+47n – 72n+144=0. n2 – 25n+144=0 n2 – 9n– 16n+144=0 n(n – 9) –16(n – 9)=0 (n – 9)(n – 16)=0 So, n=9,16. When n=9, Largest angle =a+(9 – 1)d=120°+8 × 5° = 120° + 40° = 160°< 180° Hence, n=9 is permissible When n=16, Lorgest angle =a+(16 – 1)d=120°+15 × 5° = 120° + 75° = 195°> 180°. which is not permissible as no angle in polygon can exceed 180°. Hence, number of sides in polygon, n=9. |
Class 11 Math Sequence And Series Exercise 8.3 Solutions
Ex 8.3 Class 11 Math focuses on the application of sequences and series, including harmonic progression (HP), arithmetic-geometric series, and special summation formulas. Exercise 8.3 helps build upon the concepts of arithmetic progression (AP) and geometric progression (GP) and introduces students to the relationship between these progressions. Students can check solution for all question here;
Class 11 Sequence And Series Ex 8.3 SolutionQ1. Find the 20th and nth terms of the G.P.
|
| A.1. Here, a=
=
so, an = arn-1 i.e a20=ar20-1=
and an= arn-1=
|
| Q2. Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2. |
| A.2. Given, r=2 Let a be the first term, Then, a8= 92
so,a =
= 3×210 = 31024 = 3072. |
| Q3. The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Showthat q2 = ps. |
| A.3. Let a and r be the first term and the common ratio btw G.P. So, a5= p
a8 = q
a11= r
So, L.H.S. q2 = (ar7)2 = a2r14 R.H. S. = p.s= (ar4) (ar)10 = a1+1 r4+10 = a2r14
|
| Q4. The 4th term of a G.P. is square of its second term, and the first term is – 3.Determine its 7th term. |
| A.4. Given, a = 3 Let r be the common ratio of the G.P. Then,a4 = (a2)2
|
| Q5. Which term of the following sequences: (a) 2,2√2 ,4,... is 128? (b) √3,3,3√3 ,... is729 ? (c)
|
| Q6. For what values of x, the numbers
|
| A.6. For
|
| Find the sum to indicated number of terms in each of the geometric progressions inExercises 7 to 10: Q7. 0.15, 0.015, 0.0015, ... 20 terms. |
| A.7. Here a = 0.15 =
n = 20 So, Sum to term of G.P.,
=
=
=
|
| Q8. √7 , √21 , 3√7 , ... n terms. |
| Q9. 1, – a, a2, – a3, ... n terms (if a ¹ – 1). |
| A.9.Here,
So,
=
=
|
| Q10. x3, x5, x7, ... n terms (if x ¹ ± 1). |
| Q11. Evaluate
|
| A.11.
=
=
|
| Q12. The sum of first three terms of a G.P. is
|
| A.12.Let the three terms of the G.P be
So,
=
=
And
=
=
=
=
=
=
=
=
=
=
When
When
|
| Q13. How many terms of G.P. 3, 32, 33, … are needed to give the sum 120? |
| Q14. The sum of first three terms of a G.P. is 16 and the sum of the next three terms is128. Determine the first term, the common ratio and the sum to n terms of the G.P. |
| A.14. Let a be the first term and r be the common ratio of the G.P. Then
Also
Dividing II and I we get,
r3= 8 r3 = 23 r = 2 >1 So, putting r = 2 in I we get,
And
|
| Q15. Given a G.P. with a = 729 and 7th term 64, determine S7. |
| A.15. Given, a= 729
When
=
=
=
= 2059 When
=
=
= 463 |
| Q16. Find a G.P. for which sum of the first two terms is – 4 and the fifth term is4 times the third term. |
| A.16. Let a and r be the first term and common ratio. Then,
When r =2 a (1+2)=-4 a 3 = -4
So, the G.P. is a, ar, ar2,………….
When
a = (-) = -4 a = 4 So, the reqd. by G.P. is a, ar, ar2………….
|
| Q17. If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P. |
| A.17. Let aand r be the first term and common ration of the G.P. So,
And a10 = y
Also a 16 = z
So,
and
|
| Q18. Find the sum to n terms of the sequence, 8, 88, 888, 8888… . |
| A.18. The given sequence, 8, 88, 888, 8888, …., upto xterm is not a G.P. so we can such that it will be changed to a G.P. by the following . Sum of x terms, sx = 8+ 88+888+8888 …..upto x term =
Multiplying the numerator and denumerator by 9 we get, =
=
=
=
=
=
|
| Q19. Find the sum of the products of the corresponding terms of the sequences 2, 4, 8,16, 32 and 128, 32, 8, 2,
|
| A.19. The sum of product of corresponding terms of the given Sequences =
= 256+128+69+32+16 The above is a G.P. of a = 256,
Sum required =
=
=
|
| Q20. Show that the products of the corresponding terms of the sequences a, ar, ar2,…arn– 1 and A, AR, AR2,…ARn – 1 form a G.P, and find the common ratio. |
| A.20. The product of corresponding terms of the given sequence are =
=
So, looking at the sequence forms a G.P. (above the) With common ratio =
|
| Q21. Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18. |
| A.21. Let the four numbers is G.P. be a, ar, ar2, ar3 Given,
And
Dividing II by I we get,
r = 2 So, putting r = 2 in I we get ,
|
| Q22. If the pth, qth and rth terms of a G.P. are a, b and c, respectively. Prove that aq – rbr – pcP – q= 1 |
| A.22. Let a and r be the first term and common ratio of the G.P. Then, ap = a
and aq = b
Also, ar = c
Given, L.H.S. =
A0 R[pqprq+r+qrpqr+p+prqrp+q]
= R = 1 = R.H.S |
| Q23. If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that P2 = (ab)n. |
| A.23. Given, first term and xth term and a and b Let r be the common ratio of the G.P. Then, Product of x terms, p=
p=
= (a ×a× ….n term)(r´r2´r3 …..
=
p =
So,
=
=
=
=
=
|
| Q24. Show that the ratio of the sum of first nterms of a G.P. to the sum of terms from(n + 1)th to (2n)th term is |
| A.24. Let a and r be the first term and common difference of the G.P Thus, Sum of the first on term,
Let Sn = sum of term from (n+1)th to (2n)th term =
=
[
and number of term from (2n)th to (n+1)th = n So,
=
=
|
| Q25. If a, b, c and d are in G.P. show that (a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc+ cd)2 . |
| A.25. Let r be the common ratio of the G.P. then, First term = a1 = a = a
So, L.H.S.=
=
=
=
=
R.H.S.=
=
=
= {
=
L.H.S. = R.H.S. |
| Q26. Insert two numbers between 3 and 81 so that the resulting sequence is G.P. |
| A.26. Let G1 and G2 be the two numbers between 3 and 81 so that 3, G1, G2, 81 is in G.P. So, a = 3 a4 = ar3 = 81 (when r = common ratio)
So, G1 = ar = 33=9 and G2 = ar2 3´(3)2 =27 |
| Q27. Find the value of n so that
|
| A.27. We know that, G.M between a and b = √ab Given
|
| Q28. The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio (3 + 2√2) : (3 - 2√2). |
| A.28. Let a and b be the two numbers and a>b so a-b = (+ ve) So, sum of two numbers = 6. G.M of a and b |
| Q29. If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are |
| A.29. Let a and b be the two number and a> b so a-b = (+ ve) |
| Q30. The number of bacteria in a certain culture doubles every hour. If there were 30bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ? |
| A.30. Since the numbers of bacteria doubles every hour. The number after every hour will be a G.P So, a=30 r=2
= 30×24 = 120 At end of 4th hour, a5 (r 4th term) =
= 30×24 = 30×16 = 480 Following the trend, And at the end of nth hour, an+1=
= 30 ×2n |
| Q31. What will Rs 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually? |
| A.31. Given, Principal value, amount deposited, P= ₹500 Interest Rate, R= 10 Using compound interest = simple interest +
Amount at the end of 1st year =
= ₹500×(1.1) Amount at the end of 2nd year =
=
= ₹500 (1.1)2 Similarly, Amount at the end of 3rd year = ₹500(1.1)3 So, the amount will form a G.P. ₹ 500 (1.1), ₹ 500(1.1)2 , ₹500 (1.1)3, ……….
|
| Q32. If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation. |
| A.32. Let a and b be the roots of quadratic equation So, A.M = 8
G.M. =
We know that is a quadratic equation
Which is the reqd. quadratic equation |
Class 11 Math Sequence And Series Exercise 8.4 Solutions
Class 11 Math Sequence And Series Miscellaneous Exercise Solutions
Explore exams which ask questions on Maths Ncert Solutions class 11th
Select your preferred stream
Maths Ncert Solutions class 11th Exam
Student Forum
Other Similar chapters for you
- Probability
- Statistics
- Mathematical Reasoning
- Limits and Derivatives
- Introduction to Three Dimensional Geometry
- Conic Sections
- Straight Lines
- Sequences and Series
- NCERT Maths 11th
- Permutations and Combinations
- Linear Inequalities
- Complex Numbers and Quadratic Equations
- Principle of Mathematical Induction
- Trigonometric Functions
- Relations and Functions
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test