Applications of Thermodynamics: Work, Internal Energy, and Enthalpy

Below we have listed some of the main formulas that you will be coming across while learning the application of thermodynamics in Class 11. Your school exam questions will mainly cover these.

The First Law of Thermodynamics and Internal Energy (ΔU) Concepts
Laws and processes	Formulas to remember
First Law with its general use	ΔU = q + w
Constant Volume Process	ΔU = q_v (where w=0)
Adiabatic Process	ΔU = w_ad (where q=0)
Isolated System	ΔU = 0 (where q=0 and w=0)
Isothermal Free Expansion in an Ideal Gas	ΔU = 0 (since w=0 and q=0)
Work Done (w) Concepts
Work Done TO Systems and in Processes	Formulas to remember
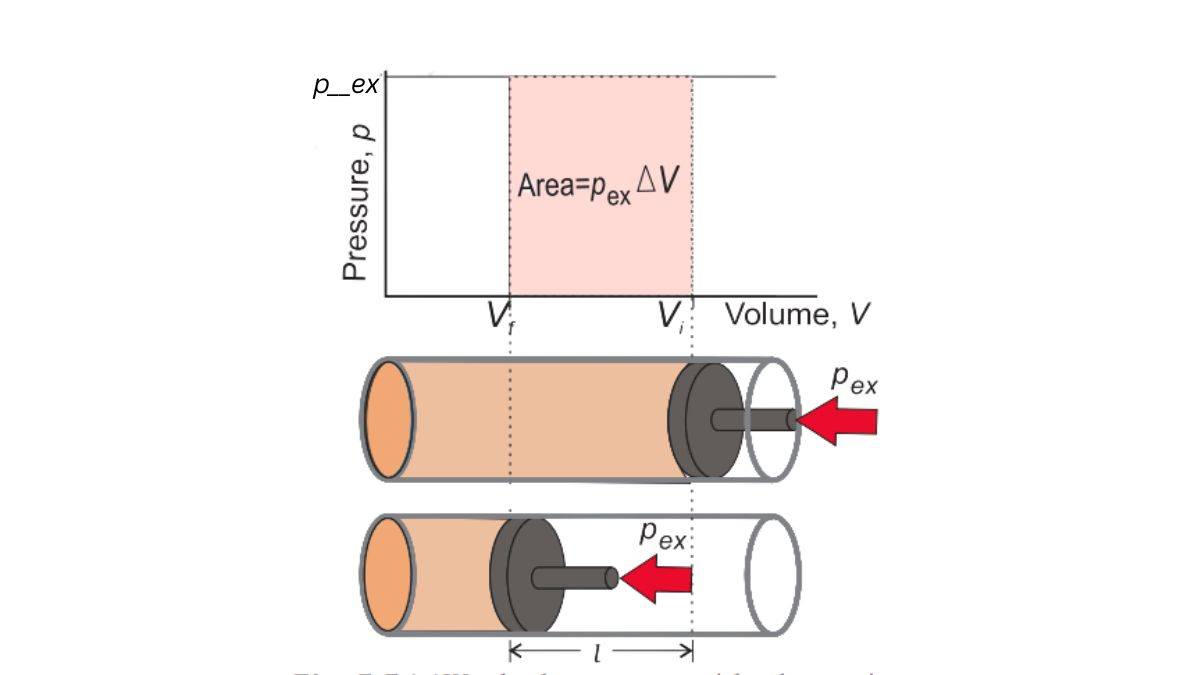
Work against Constant External Pressure when it’s irreversible	w = -p_exΔV or w = -p_ex(V_f - V_i)
Work in Finite Steps	w = -Σp_exΔV
Work Done when it’s Reversible	wᵣₑᵥ = - ∫ (pᵢₙ ± dp) dV
Isothermal Reversible Work in Ideal Gas	w = - ∫ (nRT/V) * dV
Enthalpy (H) and its Relationship with ΔU Concepts
Mathematical definition and reaction types	Formulas to remember
Definition of Enthalpy	H = U + pV
Enthalpy Change at Constant Pressure	ΔH = q_p
Enthalpy Change when it’s Finite	ΔH = ΔU + Δ(pV)
Enthalpy Change at Constant Pressure for Practicals	ΔH = ΔU + pΔV
Relationship between ΔH and ΔU in Gas Reactions	ΔH = ΔU + Δn_gRT
Heat Capacity (C) with Related Concepts
Heat capacity and relationship	Formulas to remember
Heat Transferred	q = CΔT
Heat Transferred (Specific Heat)	q = c × m × ΔT
Heat Capacity at Constant Volume	q_v = C_vΔT = ΔU
Heat Capacity at Constant Pressure	q_p = C_pΔT = ΔH
Relationship between C_p and C_v, only applicable to Ideal Gas	C_p - C_v = R

Your NCERT textbook in section 5.2.1 brings one important concept on the pressure volume work, so you don’t get confused later. The chemical thermodynamics application is better understood when we consider mechanical work as pressure-volume work. This is the real world relevance of thermodynamics that we should be learning. 

What is Pressure-Volume Work, and How is it a Chemical Thermodynamics Application?

Pressure-volume work (aka PV work or curve) as a thermodynamics application tells us how much energy is transferred due to a gas expanding or compressing when there is an external pressure.
Work, as we learn in both Physics and Chemistry Class 11, is not an abstract concept with force and displacement or distance. 

Work is a direct application of thermodynamics. 

It connects the changes of internal energy in a system with the work that gases do when compressed and expanded under some pressure from an external source. 

Before moving further, here are some key points to keep in mind in which ways work is an application of thermodynamics. 

• Note that the internal energy in a gas comes from the energy of the motion of molecules. 
• Whenever gas expands or compresses, energy transfers or converts into mechanical energy. 

In chemical thermodynamics, work shows as pressure-volume work.  And this application can show laws of thermodynamics are behind the transfer of energy in several realistic processes. We can see these in the real world, and prove it. 

Work done during compression of an ideal gas in a cylinder

This is a simple concept. Let’s look at the figure below (recreated from your NCERT textbook’s Figure 5.5a). 

 

If you have to calculate how much heat a system has, it is important to know a thermodynamics concept, enthalpy. 

The enthalpy definition in thermodynamics is:

Enthalpy is the sum of the internal energy of a system, and remains the product of the pressure and volume. 

Enthalpy and First Law of Thermodynamics: Exploring the Relationship

From the point of view of chemistry, we need to know that enthalpy changes when heat goes into or out of the thermodynamic system whenever there is a change in a reaction. 

This change of enthalpy of a reaction is seen as equivalent to the energy amount that is gained or lost within the thermodynamic system. If heat increases, enthalpy increases. The reverse also works. 

Most chemical reactions occur at constant atmospheric pressure. But not at constant volume. That lets us find a new state function, for which we have an explanation below. 

Now, if we refer to the first law of thermodynamics in Physics, we can tell that if there is constant volume, but there is a change in internal energy, that would be almost equal to the heat absorbed or released. 

Suppose, we are dealing with an increase in internal energy and the work done on the system is positive. We would be using the equation used in the 1st Law of Thermodynamics.

ΔU = q + w

Here,

ΔU is the change in the internal energy, q is the transferred heat into the system or let’s say, it’s the absorbed heat of the system, and w is the work done. This equation appears in your NCERT text as equation 5.1. 

Now since we are involved with considering atmospheric pressure to be constant, we will denote q as qp so that we are certain that pressure is involved as the variable and not temperature or volume, as said earlier. 

We will then use the equation from earlier for work as defined by the pressure-volume relationship. That would be, to reiterate, w = -pₑₓΔV.

So, the change in internal energy equation from above would look like 

ΔU = qp + (-pₑₓΔV)

Or, 

ΔU = qp -pₑₓΔV

 

When we rearrange, we would be getting

qp = ∆U + p∆V

 

To expand this so that we highlight the internal energy change from initial to final states, we get

qp = (U₂ - U₁) + p(V₂ - V₁)

Now, if we are grouping the initial and final state terms, we get 

qp = (U₂ + pV₂) - (U₁ + pV₁)

This above equation introduces us to a state function. In thermodynamics, we refer to a state function as a system’s characteristic variable, such as temperature, pressure, or volume. The value of these variables are independent of the path taken to reach that value. 

Since U, p, and V are functions of state and are independent of path, enthalpy also becomes the same.  

Instead of stating U₂ + pV₂ or U₁ + pV₁, one simpler term can be used here. That is enthalpy. That’s denoted by H.
We would write the equation for enthalpy as 

H = U + pV

Now, the equation,  qp = H₂ - H₁

Or simply put, we can use, or say the heat absorbed by the system as 

qp = ΔH

How to Represent Enthalpy for Ideal Gas

As above, we were focusing on ideal gas equation (pV = nRT), let’s use it so below for the equation for enthalpy (H = U + pV)

ΔH = ΔU  + ΔnRT

How is Enthalpy an Application of Chemical Thermodynamics?

Enthalpy brings us to the real world. The equation, ΔU = q works in sealed containers, but in the real world, we talk about heat or energy transfer in beakers or flasks. There we would need to use it. 

Enthalpy is the direct application of the first thermodynamics law. 

Another important aspect to remember is that enthalpy has sign conventions that determine the type of reaction that would further help in designing chemical equipment. 

• When ΔH is negative, heat releases from the system. That is called an exothermic reaction. In the real world, by learning that ΔH is less than zero or negative, one would be able to design a cooling system to prevent overheating. 
• When ΔH is positive, heat absorbs into the system. That’s an endothermic reaction. If ΔH is greater than zero for a heating system design build, it means more heat would be required to run it.

Intensive and Extensive Properties 

Enthalpy, as we learned from above, is the total energy or heat in the system when the atmospheric pressure is constant. Just to repeat, enthalpy is the internal energy sum and product of pressure and volume. The equation, H = U + PV, works here. 

In the branch of chemical thermodynamics, and till now, what we have learned in this article, we should be gearing up to measure changes in enthalpy. We say that mathematically, as ΔH. This is to determine how heat or energy is exchanged during chemical reactions. 

But this quantification totally depends on measuring properties that let us know total enthalpy and specific or molar enthalpy of the substance in a system. That is, we need to know two essential properties. They are intensive and extensive. 

Difference Between Extensive and Intensive Properties

A table for this topic on intensive vs extensive properties is below. 

Properties	Definition	Nature	Examples
Extensive Property	This is a thermodynamic property whose value depends on the quantity of matter that is in the system. The value could be dependent on the matter’s size as well.	It is additive in nature, simply because when you combine two systems, the extensive property will add on their own.	Some of the basic examples here would be mass, volume, internal energy, even enthalpy, and so on.
Intensive Property	This type of thermodynamic property has a value, which is independent of matter quantity or size.	This is non-additive, and it takes on the characteristic of the substance only.	Intensive property examples would be temperature (T), density, and similar.

Heat Capacity

Heat capacity is also called thermal capacity of a system that absorbs or releases heat with a change in temperature. It is understood that the heat supplied to a system will be proportional to the rise in temperature. 

If you are wondering why you’re learning heat capacity as an application of thermodynamics, just know that it helps us know how different substances respond to heat. 

The quantity of heat required can be denoted as q, while the temperature required to heat a substance would be denoted as T. We denote heat or thermal capacity as C. The mathematical relationship is

C = q/ΔT

Another thing to remember is that heat capacity is an extensive property. It depends on the type of substance and the amount of the substance that can release or absorb heat. 

To define heat capacity more accurately, we can look into heat capacity per unit of an amount of the substance. And we have two ways to do so. 

Molar Heat Capacity: It’s the heat capacity of a substance on a per mole basis. It shows the quantity of heat required to raise the temperature of one  mole of the substance by one degree.
We show that as 

C_m = C / n

n is the number of moles.

Specific Heat Capacity: It’s the heat capacity per unit mass of the substance.

So, the previous formula written as

q = c x m x ΔT

 

We discuss two conditions below that determine how heat should be measured. 

Relationship Between Constant Pressure and Constant Volume in Enthalpy

One important consideration before we move ahead here would be to measure the heat capacity of an ideal gas to explore the conditions of constant volume and constant pressure. 

What’s Heat Capacity at Constant Volume?

Here, it’s about raising the temperature by one degree when the volume is constant and unchanging. In this, no pressure-work (pV) is done, so we can say that w equals zero. 

From the First Law of Thermodynamics, when we use the formula

ΔU = q + w

Since w = 0,
We have 

ΔU = q

We can also q as q_v to denote the heat 

So, bringing the formula of heat capacity here when the volume is constant.

C = q/ΔT

q=CΔT

At constant volume, we get 

q_v = CΔT = ΔU

That means, the heat capacity at constant volume is equal to the internal energy in an ideal gas.

What’s Heat Capacity at Constant Pressure?

When there’s constant pressure, there would be a natural volume change in the ideal gas. That tells us there will be some work done. 

Now we learned from earlier that w = pΔV

Using the first law, we get

ΔU = q + w

Or, now we get when replacing work with pressure volume relation we earlier saw in this chapter

ΔU = q - pΔV

And simply rearranging 

ΔU + pΔV = q 

But we know U+ pV = H, ie, enthalpy. 

So, the heat capacity when volume changes but pressure does not is enthalpy. 

We can show use the heat capacity equation here as q = C_pΔT = ΔU + pΔV = ΔH

C_p denotes heat capacity at constant pressure. 

To further dig the relationship between heat or thermal capacity at constant pressure and constant volume, we can look at 

ΔH = ΔU + pΔV

Since we now have recognised that enthalpy (H) is C_pΔT and internal energy (U) is C_vΔT, let’s replace ΔH = ΔU + pΔV with C_pΔT = C_vΔT +  pΔV

Rearranging then will give us

pΔV = C_pΔT - C_vΔT

Now if temperature does not change in an ideal gas, we can get rid of T, and 

pΔV = C_p - C_v

In an ideal gas, pV = nRT, for one mole of gas,

So, 

R = C_p - C_v

Just know that the applications section for thermodynamics chapter class 11 chemistry is quite extensive. Questions that usually come in school exams would be mostly conceptual while there will be numerical applications for the derivations on enthalpy and internal energy. 

Conceptual and Theoretical Questions on Applications of  Thermodynamics

The scope of such questions will test your knowledge on:

• Identifying and differentiating between enthalpy and internal energy.
• Knowing how intensive and extensive properties depend on various factors. 
• Answering the right conditions for free expansion of gas under adiabatic conditions, while being clear about the reversible and irreversible processes. 

Numerical Questions on Applications of Thermodynamics

If you have been following your NCERT textbook, you will be coming across these types of numerical problems. So prepare for:

• Calculating work done as pressure-volume work when gas expands against constant external pressure.
• Measuring ΔH to ΔU for reactions that have one mole of gas.

There’s no need to struggle while you revise right before exams. You can go for our exam-ready and easy-to-learn topic pages on Class 11 Chemistry. 

Bookmark this page on NCERT Class 11 Chemistry Notes that has links for all the topics in Class 11.  Or, you can follow along the chapters and their subtopics below. 

S.No.	Chapter Name
1	Some Basic Concepts of Chemistry Notes
2	Structure of Atom Notes
3	Simplified notes on Classification of Elements and Periodicity in Properties
4	Detailed topics and notes on Chemical Bonding and Molecular Structure
5	States of Matter Gases and Liquids for Class 11 Chemistry
6	Thermodynamics Notes
7	Equilibrium Notes
8	Redox Reactions Notes
9	The s-Block Element Notes
10	The p-Block Element Notes
11	Organic Chemistry - Some Basic Principles and Techniques Notes
12	Hydrocarbons Notes
13	Environmental Chemistry Notes

 

All in one place, prepared and curated for easy learning and exam practice, find NCERT Solutions for Class 11 Chemistry. 

Class 11th Chemistry Chapter-wise NCERT Solutions

Chapter 1 Some Basic Concepts of Chemistry NCERT Solutions

Chapter 2 Structure of Atom NCERT Solutions

Chapter 3 Classification of Elements and Periodicity in Properties NCERT Solutions

Chapter 4 Chemical Bonding and Molecular Structure NCERT Solutions

Chapter 5 Thermodynamics NCERT Solutions

Chapter 6 Equilibrium NCERT Solutions

Chapter 7 Redox Reactions NCERT Solutions

Chapter 8 Organic Chemistry – Some Basic Principles and Techniques NCERT Solutions

Chapter 9 Hydrocarbons NCERT Solutions

A Note on the Reviewer

For this article reviewed on the applications of thermodynamics in chemistry, we have Raghvendra Kumar Yadav. A bit about him is below. 

Raghvendra Kumar Yadav is an experienced Physics subject matter expert, whose work covers 10 years in teaching along with curriculum-aligned content reviewing. Clearing competitive exams, including JEE Mains and GATE, his teaching shows hands-on familiarity with exam patterns and the most effective strategies for learners to prepare.Raghvendra's teaching portfolio now extends to helping students prepare for JEE Mains and NEET exams, while helping them become confident when approaching Class 11 and 12 exams. At Shiksha, he ensures all educational content on Physics and Chemistry has high academic rigour with high accuracy and direct CBSE-guided exam alignment.