- What are kinematics equations?
- Inverse kinematics
- Kinematics Equations
- The kinematic equation for uniformly accelerated equation
- Rotational Kinematics Equations
- Kinematics equation of motion for class 12
- Illustrated Examples
- FAQs on kinematics equations of motion
What are kinematics equations?
Kinematics is a branch of physics and is defined as the relationship between space and time. It ignores the cause of the motion caused by space and time. Kinematics equations are used to identify the unknown body's motions. Kinematic equations are linked with five variables which are listed below:
- Initial velocity denoted as V0
- Displacement referred to as Δx
- Time travel was written as t
- Final velocity as v
- Constant acceleration is written as a
If one of the two variables are given, kinematics equations can derive the others using limited variables.
Inverse kinematics
The reverse of kinematics is called inverse kinematics. It is considered complicated compared to simple kinematics equations and might produce more than one solution.
Kinematics Equations
The kinematics equations can be segregated into four sections which are listed below:
- V = v0 + at
- Δ x = (v + v0 / 2) t
- Δ x = v0 t + ½ at2
V2 = v2o + 2a Δx
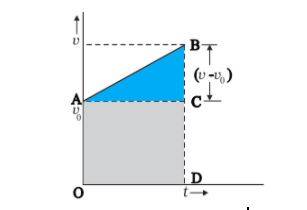
The kinematic equation for uniformly accelerated equation
The diagrammatic equation of the kinematic equation which is uniformly accelerated is as below –
Rotational Kinematics Equations
Most equations deal with the linear or translational kinematics equations and It can be identified with the motion of the body. However, there is another option in the branch of physics, which is rotational kinematics equations. Rotational kinematics equations are somewhat similar to the equations discussed above. The only difference is the changes in the variables. The rotational kinematics equations variables are listed below –
- Unlike in linear kinematic equations, angular is used here instead of acceleration.
- Change in angle is used here, instead of displacement.
- Initial and final angular velocity is used instead of initial and final velocities.
- Time is constant as it was in linear kinematic equations.
Kinematics equation of motion for class 12
The chapter of the introduction of motion holds a weightage of 6 marks in total, as per the new pattern of 2021. It includes 3 questions, one objective type question of 1 mark, one very short question of 2 marks, and one short question of 3 marks.
Illustrated Examples
Example 1: Illustrate The diagrammatic equation of the Kinematic equation which is uniformly accelerated.
Answer: The diagrammatic equation of the kinematic equation which is uniformly accelerated is as below –
Image source – ncert
Example 2: Illustrate the 5 variables in the Kinematics equation.
Answer: Kinematic equations are linked with five kinematic variables which are listed below:
- Initial velocity denoted as V0
- Displacement referred to as Δx
- Time travel was written as t
- Final velocity as v
- Constant acceleration is written as a
Example 3: State the only constant parameter between linear kinematics and rotational kinematics.
Answer: Time is constant in rotational kinematics as it was in the linear kinematic equation.
FAQs on kinematics equations of motion
1): How do you denote initial velocity in the Kinematics equation?
2): How do you denote displacement in the Kinematics equation?
3): What do you understand from the Kinematics equation?
4): State inverse Kinematics’ equation.
5): What's the equation for the Kinematics equation?
Physics Motion Exam
Student Forum
Other Topics under this Chapter
- Rotation and Revolution
- Uniform and Non Uniform Motion
- Derivation of Centripetal Acceleration
- Derivation of Escape Velocity
- Drift Velocity Derivation
- Hubbles Law
- Kinematics of Machines
- Kinematics Equations of Motion
- Derivation of Compton Effect
- Derive Equation of Motion by Calculus method
- Terminal Velocity derivation
- Centripetal and Centrifugal Force
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test