Class 11 Physics NCERT Solutions Chapter 10 Thermal Properties of Matter (Free PDF)

Q: 11.10 A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction ? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1, steel = 1.2 × 10–5 K–1 ).

11.10 Initial temperature, T1 = 40.0°C, Final temperature, T2 = 250°C, ? T = T2 - T1 = 210°C Initial length of the brass rod at T1 , lb = 50 cm, Initial diameter of the brass rod at T1 , d1 = 3 mm Length of the steel rod ls=50cm For the expansion of the brass rod, we have: Changeinlength(?lb)Originallength(lb) = αb?T , then ?lb = 50 ×2.0×10-5×210 = 0.21 cm For the expansion of the steel rod, we have: Changeinlength(?ls)Originallength(ls) = αb?T , then ?ls = 50 ×1.2×10-5×210 = 0.126 cm Total change in length = 0.21 + 0.126 = 0.336 cm Since the rods are free at the end, no thermal stress developed.

Q: 11.1 The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.

11.1 Kelvin and Celsius scales are related as Tc = Tk - 273.15 …..(i), Where Tc= temperature in Celsius scale and Tk = temperature in Kelvin scale Celsius and Fahrenheit scales are related as Tc5 = Tf-329 , where Tf = temperature in Fahrenheit scale (a) For Neon, Tk = 24.57. Hence Tc = 24.57 – 273.15 = -248.58 degree Celsius Tf=95×Tc+32 = 95×(-248.58)+32 = -415.44 degree Fahrenheit (b) For Carbon dioxide, Tk = 216.55. Hence Tc = 216.55 – 273.15 = -56.6 degree Celsius Tf=95×Tc+32 = 95×(-56.6)+32 = -69.88 degree Fahrenheit

Q: 11.2 Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between TA and TB ?

11.2 Triple point of water on absolute scale A, T1 = 200 A Triple point of water on absolute scale B, T2 = 350 B Triple point of water on absolute Kelvin scale, Tk = 273.15 K The temperature 273.15 K on Kelvin scale is equivalent to 200 on absolute scale A T1=Tk 200 A = 273.15 K, Therefore A = 273.15200 Similarly B = 273.15350 If TA is the triple point of water on scale A and TB is the triple point of water on scale B, we have 273.15200 *TA = 273.15350* TB TA= 200350* TB = 47* TB

Q: 11.3 The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law : R = Ro [1 + α(T – T0 )] The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?

11.3 It is given that R = R0 [1 + α(T – T0 )] ………(i) Where Ro and To are the initial resistance and temperature and R and T are the final resistance and temperature. At the triple point of water, To = 273.15 K, R0 = 101.6 Ω At normal melting point of lead, T = 600.5 K, R = 165.5 Ω Substituting these values in equation (i), we get 165.5 = 101.6 [1 + α(600.5 – 273.15 )] 165.5101.6 = 1 + 327.35 α, or α = 0.629327.35 = 1.92 ×10-3 K-1 When R = 123.4 Ω, T can be calculated as 123.4 = 101.6 [1 + 1.92 ×10-3× (T – 273.15 )] 1.214 = 1 + T1.92 ×10-3 - 1.92 ×10-3× 273.15 T = 384.6 K

Q: 11.4 Answer the following : (a) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale) ? (b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale ? (c) The absolute temperature (Kelvin scale) T is related to the temperature tc on the Celsius scale by tc = T – 273.15.Why do we have 273.15 in this relation, and not 273.16 ? (d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?

11.4 (a) The triple point of water has a unique value of 273.16 K, irrespective of pressure and volume. Whereas, melting point of ice and boiling point of water, the temperature value depends on pressure and volume. (b) The other fixed point on Kelvin scale is 0 K. (c) The temperature 273.16 K is the triple point of water, it is not the melting point of ice. The melting point of ice is specified in Celsius scale as 0 °C. Hence the absolute temperature in Kelvin scale, Tk is related to temperature Tc in Celsius scale as Tc=Tk-273.15 (d) Let Tf and Tk be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know Tf-329 = Tk-273.155 ……(i) Let Tf1 and Tk1 be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know Tf1-329 = Tk1-273.155 ……(ii) It is given Tk1-Tk = 1 K Now subtracting (i) from (ii), we get Tf1-329 - Tf-329 = Tk1-273.155-Tk-273.155 Tf1-Tf9 = Tk1-Tk5 Tf1-Tf = 95 Triple point of water = 273.16 K Hence triple point of water in the absolute scale = 273.16 × 95 = 491.69

Updated on Aug 12, 2025 15:44 IST

By Pallavi Pathak, Assistant Manager Content

In Class 11 Thermal Properties of Matter, the students will learn about heat - what heat is and how we can measure it. The chapter talks about the various processes by which heat flows from one body to another. It also includes what happens when the water boils or freezes, and a great deal of heat is flowing into (boiling) and out of it (freezing), then also its temperature does not change.
The subject matter experts at Shiksha have created the Thermal Properties of Matter Class 11 NCERT solutions. It offers accurate and reliable study material to students to prepare for the Class 11 exams, CBSE Board exam, and other entrance tests like JEE Main and NEET. The chapter covers calorimetry, specific heat capacity, thermal expansion, and more.
To get access to the chapter-wise PDF, important topics, and weightage information of Class 11 Physics, check here - Class 11 Physics Notes.

Table of content

NCERT Class 11 Physics Chapter 10 Thermal Properties of Matter: Key Topics, Weightage
NCERT Physics Class11th Solution PDF for Thermal Properties of Matter
NCERT Physics Class 11th Thermal Properties of Matter Questions and Answers

NCERT Class 11 Physics Chapter 10 Thermal Properties of Matter: Key Topics, Weightage

While preparing for the Thermal Properties of Matter Class 11, students must focus on the following key topics: thermal expansion (linear, area, volume), heat temperature, calorimetry, specific heat capacity, and heat transfer. See below the topics covered in this chapter:

Exercise	Topics Covered
10.1	Introduction
10.2	Temperature and Heat
10.3	Measurement of Temperature
10.4	Ideal-gas Equation and Absolute Temperature
10.5	Thermal Expansion
10.6	Specific Heat Capacity
10.7	Calorimetry
10.8	Change of State
10.9	Heat Transfer
10.10	Newton's Law of Cooling

Class 11 Thermal Properties of Matter Weightage in NEET, JEE Main exam

Exam	Number of Questions	Weightage
JEE Main	1-3 questions	2-3%
NEET	1 question	1%

NCERT Physics Class11th Solution PDF for Thermal Properties of Matter

Download the Thermal Properties of Matter NCERT PDF from the link given below. It contains detailed and step-by-step solutions to all questions of this chapter to help you prepare for your examinations.

Download Here: NCERT Solution for Class XI Physics Chapter Thermal Properties of Matter PDF

Check here for NCERT Solutions Class 11 and 12 of all three subjects, including Chemistry, Physics, and Maths. You will also get the key topics and chapter-wise PDFs in one place.

NCERT Physics Class 11th Thermal Properties of Matter Questions and Answers

Q.11.1 The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.

Ans.11.1 Kelvin and Celsius scales are related as

$T_{c}$ = $T_{k}$ - 273.15 …..(i),

Where $T_{c} =$ temperature in Celsius scale and $T_{k}$ = temperature in Kelvin scale

Celsius and Fahrenheit scales are related as

$\frac{T_{c}}{5}$ = $\frac{T_{f} - 32}{9}$ , where $T_{f}$ = temperature in Fahrenheit scale

(a) For Neon, $T_{k}$ = 24.57. Hence $T_{c}$ = 24.57 – 273.15 = -248.58 degree Celsius

$T_{f} = \frac{9}{5} \times T_{c} + 32$ = $\frac{9}{5} \times (- 248.58) + 32$ = -415.44 degree Fahrenheit

(b) For Carbon dioxide, $T_{k}$ = 216.55. Hence $T_{c}$ = 216.55 – 273.15 = -56.6 degree Celsius

$T_{f} = \frac{9}{5} \times T_{c} + 32$ = $\frac{9}{5} \times (- 56.6) + 32$ = -69.88 degree Fahrenheit

Q.11.2 Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B ?

Ans.11.2 Triple point of water on absolute scale A, $T_{1}$ = 200 A

Triple point of water on absolute scale B, $T_{2}$ = 350 B

Triple point of water on absolute Kelvin scale, $T_{k}$ = 273.15 K

The temperature 273.15 K on Kelvin scale is equivalent to 200 on absolute scale A

$T_{1} = T_{k}$

200 A = 273.15 K , Therefore A = $\frac{273.15}{200}$

Similarly B = $\frac{273.15}{350}$

If $T_{A}$ is the triple point of water on scale A and $T_{B}$ is the triple point of water on scale B, we have

$\frac{273.15}{200}$ $\times T_{A}$ = $\frac{273.15}{350} \times$ $T_{B}$

$T_{A} =$ $\frac{200}{350} \times$ $T_{B}$ = $\frac{4}{7} \times$ $T_{B}$

Q.11.3 The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law :

R = Ro [1 + α(T – $T_{0}$ )]

The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?

Ans.11.3: It is given that R = $R_{0}$ [1 + α(T – $T_{0}$ )] ………(i)

Where Ro and To are the initial resistance and temperature and R and T are the final resistance and temperature.

At the triple point of water, To = 273.15 K, $R_{0}$ = 101.6 Ω

At normal melting point of lead, T = 600.5 K, R = 165.5 Ω

Substituting these values in equation (i), we get

165.5 = $101.6$ [1 + α(600.5 – $273.15$ )]

$\frac{165.5}{101.6}$ = 1 + 327.35 α, or α = $\frac{0.629}{327.35}$ = 1.92 $\times 10^{- 3}$ $K^{- 1}$

When R = 123.4 Ω, T can be calculated as

123.4 = $101.6$ [1 + 1.92 $\times 10^{- 3} \times$ (T – $273.15$ )]

1.214 = 1 + T1.92 $\times 10^{- 3}$ - 1.92 $\times 10^{- 3} \times$ 273.15

T = 384.6 K

Q.11.4 Answer the following :

(a) The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale) ?

(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale ?

(c) The absolute temperature (Kelvin scale) T is related to the temperature $t_{c}$ on the Celsius scale by $t_{c}$ = T – 273.15

Why do we have 273.15 in this relation, and not 273.16 ?

(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?

Ans.11.4

(a) The triple point of water has a unique value of 273.16 K, irrespective of pressure and volume. Whereas, melting point of ice and boiling point of water, the temperature value depends on pressure and volume.

(b) The other fixed point on Kelvin scale is 0 K.

(c) The temperature 273.16 K is the triple point of water, it is not the melting point of ice. The melting point of ice is specified in Celsius scale as 0 $° C .$ Hence the absolute temperature in Kelvin scale, $T_{k}$ is related to temperature $T_{c}$ in Celsius scale as

$T_{c} = T_{k} - 273.15$

(d) Let $T_{f}$ and $T_{k}$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_{f} - 32}{9}$ = $\frac{T_{k} - 273.15}{5}$ ……(i)

Let $T_{f 1}$ and $T_{k 1}$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_{f 1} - 32}{9}$ = $\frac{T_{k 1} - 273.15}{5}$ ……(ii)

It is given $T_{k 1} - T_{k}$ = 1 K

Now subtracting (i) from (ii), we get

$\frac{T_{f 1} - 32}{9}$ - $\frac{T_{f} - 32}{9}$ = $\frac{T_{k 1} - 273.15}{5} - \frac{T_{k} - 273.15}{5}$

$\frac{T_{f 1} - T_{f}}{9}$ = $\frac{T_{k 1} - T_{k}}{5}$

$T_{f 1} - T_{f}$ = $\frac{9}{5}$

Triple point of water = 273.16 K

Hence triple point of water in the absolute scale = 273.16 $\times$ $\frac{9}{5}$ = 491.69

Commonly asked questions

11.10 A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction ? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10^–5 K^–1, steel = 1.2 × 10^–5 K^–1 ).

11.10 Initial temperature, $T_{1}$ = 40.0°C, Final temperature, $T_{2}$ = 250°C, $?$ T = $T_{2}$ - $T_{1}$ = 210°C

Initial length of the brass rod at $T_{1}$ , $l_{b}$ = 50 cm, Initial diameter of the brass rod at $T_{1}$ , $d_{1}$ = 3 mm

Length of the steel rod $l_{s} = 50 c m$

For the expansion of the brass rod, we have:

$\frac{C h a n g e i n l e n g t h (? l_{b)}}{O r i g i n a l l e n g t h (l_{b)}}$ = $α_{b} ? T$ , then $? l_{b}$ = 50 $\times 2.0 \times 10^{- 5} \times 210$ = 0.21 cm

For the expansion of the steel rod, we have:

$\frac{C h a n g e i n l e n g t h (? l_{s)}}{O r i g i n a l l e n g t h (l_{s})}$ = $α_{b} ? T$ , then $? l_{s}$ = 50 $\times 1.2 \times 10^{- 5} \times 210$ = 0.126 cm

Total change in length = 0.21 + 0.126 = 0.336 cm

Since the rods are free at the end, no thermal stress developed.

11.1 The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.

11.1 Kelvin and Celsius scales are related as

$T_{c}$ = $T_{k}$ - 273.15 …..(i),

Where $T_{c} =$ temperature in Celsius scale and $T_{k}$ = temperature in Kelvin scale

Celsius and Fahrenheit scales are related as

$\frac{T_{c}}{5}$ = $\frac{T_{f} - 32}{9}$ , where $T_{f}$ = temperature in Fahrenheit scale

(a) For Neon, $T_{k}$ = 24.57. Hence $T_{c}$ = 24.57 – 273.15 = -248.58 degree Celsius

$T_{f} = \frac{9}{5} \times T_{c} + 32$ = $\frac{9}{5} \times (- 248.58) + 32$ = -415.44 degree Fahrenheit

(b) For Carbon dioxide, $T_{k}$ = 216.55. Hence $T_{c}$ = 216.55 – 273.15 = -56.6 degree Celsius

$T_{f} = \frac{9}{5} \times T_{c} + 32$ = $\frac{9}{5} \times (- 56.6) + 32$ = -69.88 degree Fahrenheit

11.2 Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B ?

11.2 Triple point of water on absolute scale A, $T_{1}$ = 200 A

Triple point of water on absolute scale B, $T_{2}$ = 350 B

Triple point of water on absolute Kelvin scale, $T_{k}$ = 273.15 K

The temperature 273.15 K on Kelvin scale is equivalent to 200 on absolute scale A

$T_{1} = T_{k}$

200 A = 273.15 K, Therefore A = $\frac{273.15}{200}$

Similarly B = $\frac{273.15}{350}$

If $T_{A}$ is the triple point of water on scale A and $T_{B}$ is the triple point of water on scale B, we have

$\frac{273.15}{200}$ $* T_{A}$ = $\frac{273.15}{350} *$ $T_{B}$

$T_{A} =$ $\frac{200}{350} *$ $T_{B}$ = $\frac{4}{7} *$ $T_{B}$

11.3 The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law :

R = Ro [1 + α(T – $T_{0}$ )]

The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?

11.3 It is given that R = $R_{0}$ [1 + α(T – $T_{0}$ )] ………(i)

Where Ro and To are the initial resistance and temperature and R and T are the final resistance and temperature.

At the triple point of water, To = 273.15 K, $R_{0}$ = 101.6 Ω

At normal melting point of lead, T = 600.5 K, R = 165.5 Ω

Substituting these values in equation (i), we get

165.5 = $101.6$ [1 + α(600.5 – $273.15$ )]

$\frac{165.5}{101.6}$ = 1 + 327.35 α, or α = $\frac{0.629}{327.35}$ = 1.92 $\times 10^{- 3}$ $K^{- 1}$

When R = 123.4 Ω, T can be calculated as

123.4 = $101.6$ [1 + 1.92 $\times 10^{- 3} \times$ (T – $273.15$ )]

1.214 = 1 + T1.92 $\times 10^{- 3}$ - 1.92 $\times 10^{- 3} \times$ 273.15

T = 384.6 K

11.4 Answer the following :

(c) The absolute temperature (Kelvin scale) T is related to the temperature $t_{c}$ on the Celsius scale by $t_{c}$ = T – 273.15.Why do we have 273.15 in this relation, and not 273.16 ?

(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?

11.4 (a) The triple point of water has a unique value of 273.16 K, irrespective of pressure and volume. Whereas, melting point of ice and boiling point of water, the temperature value depends on pressure and volume.

(b) The other fixed point on Kelvin scale is 0 K.

$T_{c} = T_{k} - 273.15$

(d) Let $T_{f}$ and $T_{k}$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_{f} - 32}{9}$ = $\frac{T_{k} - 273.15}{5}$ ……(i)

Let $T_{f 1}$ and $T_{k 1}$ be the temperature in Fahrenheit and absolute scale. From the co-relation of the scale we know

$\frac{T_{f 1} - 32}{9}$ = $\frac{T_{k 1} - 273.15}{5}$ ……(ii)

It is given $T_{k 1} - T_{k}$ = 1 K

Now subtracting (i) from (ii), we get

$\frac{T_{f 1} - 32}{9}$ - $\frac{T_{f} - 32}{9}$ = $\frac{T_{k 1} - 273.15}{5} - \frac{T_{k} - 273.15}{5}$

$\frac{T_{f 1} - T_{f}}{9}$ = $\frac{T_{k 1} - T_{k}}{5}$

$T_{f 1} - T_{f}$ = $\frac{9}{5}$

Triple point of water = 273.16 K

Hence triple point of water in the absolute scale = 273.16 $\times$ $\frac{9}{5}$ = 491.69

11.5 Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made:

Temperature Pressure Pressure

thermometer A thermometer B

Triple-point of water 1.250 × 10⁵ Pa 0.200 × 10⁵ Pa

Normal melting point 1.797 × 10⁵ Pa 0.287 × 10⁵ Pa

of sulphur

(a) What is the absolute temperature of normal melting point of sulphur as read by thermometers A and B ?

(b) What do you think is the reason behind the slight difference in answers of thermometers A and B? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?

11.5 (a) For Thermometer A

Triple point of water, T = 273.16 K

At this temperature, the pressure in thermometer A , $P_{A}$ = 1.250 $\times 10^{5}$ Pa

Let $T_{1}$ be the temperature for the normal melting point of sulphur and $P_{1}$ be the corresponding pressure. It is given, $P_{1}$ = 1.797 $\times 10^{5}$ Pa

From Charles’ law, we get $\frac{P_{A}}{T}$ = $\frac{P_{1}}{T_{1}}$ , $T_{1}$ = $\frac{P_{1} \times T}{P_{A}}$ = $\frac{1.797 \times 10^{5} \times 273.16}{1.250 \times 10^{5}}$ = 392.69 K

For Thermometer B

Triple point of water, T = 273.16 K

At this temperature, the pressure in thermometer B , $P_{B}$ = 0.2 $\times 10^{5}$ Pa

Let $T_{1}$ be the temperature for the normal melting point of sulphur and $P_{1}$ be the corresponding pressure. It is given, $P_{1}$ = 0.287 $\times 10^{5}$ Pa

From Charles’ law, we get $\frac{P_{B}}{T}$ = $\frac{P_{1}}{T_{1}}$ , $T_{1}$ = $\frac{P_{1} \times T}{P_{B}}$ = $\frac{0.287 \times 10^{5} \times 273.16}{0.2 \times 10^{5}}$ = 391.98 K

(b) The oxygen and hydrogen gas present in thermometers A and B respectively are not perfect ideal gas, hence there is a slight difference in readings.

(c) To reduce the difference between two readings, the measurement should be carried out at low pressure so that gases behave like an ideal gas.

11.6 A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day ? What is the length of the same steel rod on a day when the temperature is 27.0 °C ? Coefficient of linear expansion of steel = 1.20 × 10^–5 K^–1 .

11.6 Length of the steel tape, l = 1 m = 100 cm, At temperature T = 27 $°$ C

Coefficient of linear expansion of steel $α$ = 1.2 $\times 10^{- 5}$ / K

Let $l_{1} = 63 c m$ be the length of the steel rod at temperature $T_{1}$ = 45.0 °C and

$l_{2}$ be the length of the steel rod and l’ be the length of the steel tape at 45.0 °C

We have l’ = l + $α l (T_{1} - T)$ = 100 + 1.2 $\times 10^{- 5} \times 100 \times$ (45-27) = 100.0216 cm

$l_{2}$ can be calculated as $l_{2}$ = $\frac{l'}{l} \times 63$ = 63.0136 cm

11.7 A large steel wheel is to be fitted on to a shaft of the same material. At 27 °C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range : $α_{s t e e l}$ = 1.20× $10^{- 5}$ $K^{- 1}$

11.7 Given, temperature $T_{1}$ = 27 °C = 27 + 273.16 K = 300.16 K

Outer dia of the shaft at temp $T_{1}$ , $d_{1}$ = 8.7 cm

Diameter of the central hole of the wheel, $d_{2}$ = 8.69 cm

The change in diameter, Δd= $d_{2} - d_{1} =$ 8.69 – 8.7 = $-$ 0.01 cm

After the shaft is cooled in dry ice, its temperature becomes $T_{2}$ . It can be calculated from the relation

Δd= $d_{1} \times α_{s t e e l}$ ( $T_{2} - T_{1})$

-0.01 = 8.7 $\times 1.20 \times 10^{- 5} (T_{2} - 300)$

$T_{2} - 300$ = -95.78

$T_{2}$ = 204.22 K = -68.94 $?$

11.8 A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C?

Coefficient of linear expansion of copper = 1.70 × 10^–5 K^–1.

11.8 Initial temperature, $T_{1}$ = 27.0 °C, Initial diameter of the hole, $d_{1}$ = 4.24 cm

Final temperature, $T_{2}$ = 227.0 °C, Final diameter of the hole $= d_{2}$

Coefficient of linear expansion of copper, $α_{c o p p e r}$ = 1.70 $\times 10^{- 5}$ K–1

We know

$\frac{C h a n g e i n a r e a (? A)}{O r i g i n a l a r e a (A)}$ = $β ?$ T where $β$ is the coefficient of superficial expansion, $β = 2 α_{c o p p e r}$

$\frac{(π \frac{d_{2}^{2}}{4} - π \frac{d_{1}^{2}}{4})}{π \frac{d_{1}^{2}}{4}}$ = $2 α_{c o p p e r} ?$ T

$\frac{d_{2}^{2} - d_{1}^{2}}{d_{1}^{2}}$ = $2 α_{c o p p e r} ?$ T

$\frac{d_{2}^{2}}{d_{1}^{2}}$ - 1= $2 α_{c o p p e r} (T_{2} - T) =$ 2 $\times$ 1.70 $\times 10^{- 5}$ (227-27) = 6.8 $\times 10^{- 3}$

$d_{2}^{2} = 1.0068 \times 4.24 \times 4.24$

$d_{2}$ = 4.2544 cm

So change in diameter = 4.2544 – 4.24 = 0.01439 cm

Diameter increase by 1.44 $\times 10^{- 2}$ cm

11.9 A brass wire 1.8 m long at 27°C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of –39 °C, what is the tension developed in the wire, if its diameter is 2.0 mm ? Co-efficient of linear expansion of brass = 2.0 × 10^–5 K–1; Young’s modulus of brass = 0.91 × 10¹¹ Pa.

11.9 Initial temperature, $T_{1}$ = 27°C, Length of the wire $l_{1}$ at $T_{1}$ = 1.8 m

Final temperature, $T_{2}$ = -39°C

Diameter of the wire, d = 2.0 mm = 2 $\times 10^{- 3}$ m

Coefficient of linear expansion of brass, $α = 2 \times 10^{- 5}$ /K

Youngs’ modulus of brass, Y = 0.91 $\times 10^{11}$ Pa

Let the tension developed be F

We know Youngs’ modulus = $\frac{S t r e s s}{S t r a i n}$ = $\frac{\frac{F}{A}}{\frac{? L}{L}} = Y$

Y $\times \frac{? L}{L}$ = $\frac{F}{A}$ or F = $\frac{A Y ? L}{L}$

Here, A = cross-sectional area of the wire = $\frac{π}{4} d^{2}$ = $\frac{π}{4} {(2 \times 10^{- 3})}^{2}$ $m^{2}$ = 3.1416 $\times 10^{- 6} m^{2}$

Now $? L$ can be written as $? L$ = $α L (T_{2} - T_{1})$ = ( $2 \times 10^{- 5}) \times L \times (- 39 - 27)$ = -1.32 $\times 10^{- 3}$ L

Substituting all values, we get

F = (3.1416 $\times 10^{- 6} \times 0.91 \times 10^{11} \times (- 1.32 \times 10^{- 3})$ = -377.37 N

11.11 The coefficient of volume expansion of glycerin is 49 × 10^–5 K^–1. What is the fractional change in its density for a 30 °C rise in temperature ?

11.11 Coefficient of volume expansion of glycerin, $α_{V}$ = 49 $\times 10^{- 5}$ /K

Rise in temperature, $? T$ = 30°C

Fractional change in volume = $\frac{? V}{V}$

We can write, $\frac{? V}{V}$ = $α_{V} \times ? T$ = 49 $\times 10^{- 5} \times 30$ = 0.0147 ……(i)

If the final volume is $V_{2}$ and initial volume is $V_{1}$ , then

$\frac{? V}{V}$ = $\frac{V_{2} - V_{1}}{V_{1}}$

$V_{2} = \frac{m}{ρ_{2}}$ and $V_{1} = \frac{m}{ρ_{1}}$ where $ρ_{1}$ & $ρ_{2}$ are initial and final densities

$\frac{? V}{V}$ = $\frac{V_{2} - V_{1}}{V_{1}}$ = $\frac{ρ_{2} - ρ_{1}}{ρ_{1}}$ = fractional change in density = 0.0147 = 1.47 $\times$ $10^{- 2}$

11.12 A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings. Specific heat of aluminium = 0.91 J g^–1 K^–1.

11.12 Power of the drilling machine, P = 10 kW= 10 $\times 10^{3}$ W

Mass of the Aluminium block, m = 8.0 kg = 8 $\times 10^{3}$ gm

Time for which the machine is used, t = 2.5 minute = 2.5 $\times 60$ s = 150 s

Specific heat of Aluminium, c = 0.91 J/gK

Let the rise of temperature in the block after drilling be $δ$ T

Total energy consumed by the drilling machine= P $\times t$ = 10 $\times 10^{3} \times 150$ J = 1.5 $\times 10^{6}$ J

It is given 50% of energy is useful.

So useful energy, $? Q$ = 50% of Pt= 0.5 $\times$ 1.5 $\times 10^{6} =$ 7.5 $\times 10^{5}$ J

We know, $? Q$ = mc $?$ T or T = $\frac{? Q}{m c}$ = $\frac{7.5 \times 10^{5}}{8 \times 10^{3} \times 0.91}$ = 103 $?$

Therefore 2.5 minute drilling will raise the block temperature by 103 $?$

11.13 A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500 °C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39 J g^–1 K^–1; heat of fusion of water = 335 J g^–1 ).

11.13 Mass of the copper block, m = 2.5 kg = 2.5 $\times 10^{3}$ gm

Rise in temperature of the copper block, $?$ T = 500°C

Specific heat of the copper, C = 0.39 g–1 K–1

Heat of fusion of water, L = 335 J g–1

The maximum heat the copper block can lose, Q = mc $?$ T = 2.5 $\times 10^{3} \times 0.39 \times 500$ = 487500 J

Let $m_{1}$ gm be the mass of the ice, which will melt because of the copper block.

Heat gained by ice block = Q = $m_{1} L$

$m_{1} = \frac{Q}{L}$ = $\frac{487500}{335}$ g = 1455.22 gm = 1.45 kg

11.14 In an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150 °C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27 °C. The final temperature is 40 °C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal?

11.14 Mass of the metal, m = 0.20 kg = 200 g

Initial temperature of the metal, $T_{1}$ = 150 °C, Final temperature of the metal, $T_{2}$ = 40 °C

The water equivalent mass of the calorimeter, m’ = 0.025 kg = 25 g

Volume of water, V = 150 cm3

Mass of water, M at T = 27 °C, = 150 $\times 1 = 150 g$

Fall in metal temperature, $?$ T = $T_{1} - T_{2}$ = 150 – 40 = 110 °C

Specific heat of water, $C_{w}$ = 4.186 J/g/ $°$ K

Let the specific heat of metal = C

Then, heat loss by the metal, $θ$ = mC $?$ T ……. (i)

Rise in the water of the calorimeter system $?$ T’ = 40 – 27 = 13°C

Heat gained by the water and calorimeter system; $θ'$ = (M + m’) $C_{w} ?$ T’ …… (ii)

Now heat lost by the metal = heat gained by the water and calorimeter system

mC $?$ T = (M + m’) $C_{w} ?$ T’

C = $\frac{(M + m ’) C_{w} ? T ’}{m ? T}$ = $\frac{(150 + 25) \times 4.186 \times 13}{200 \times 110}$ = 0.433 J/g/ $°$ K

11.15 Given below are observations on molar specific heats at room temperature of some common gases.

Gas Molar specific heat (Cv )

(cal mo1^–1 K^–1)

Hydrogen 4.87

Nitrogen 4.97

Oxygen 5.02

Nitric oxide 4.99

Carbon monoxide 5.01

Chlorine 6.17

The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine ?

11.15 The gases listed above are diatomic. Besides the translational degree of freedom, they have other degrees of freedom. Heat must be supplied to increase the temperature of these gases. This increases the average energy of all the modes of motion. Hence the molar specific heat of diatomic gases is more than that of monatomic gases.

If only rotational mode of motion considered, then the molar specific heat of a diatomic gas

= $\frac{5}{2}$ R = $\frac{5}{2} * 1.98$ = 4.95 cal mo1^–1 K^–1

With the exception of Chlorine, all the observations given above agrees with ( $\frac{5}{2}$ R). This is because at room temperature, chlorine also has vibrational modes besides rotational and translational modes of motion.

11.16 A child running a temperature of 101°F is given an antipyrin (i.e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to 98°F in 20 minutes, what is the average rate of extra evaporation caused, by the drug. Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of human body is approximately the same as that of water, and latent heat of evaporation of water at that temperature is about 580 cal g ^–1.

11.16 Initial body temp of the child, $T_{1}$ = 101°F

Final body temp of the child, $T_{2}$ = 98°F

Change in temperature, $?$ T = $T_{1} - T_{2} = (101 ° F -$ 98°F) = 3 °F = $\frac{5}{9}$ (3-32) $°$ C = 1.666 $?$

Time taken t achieve this temperature, t = 20 min

Specific heat of human body = Specific heat of water, c = 1000 cal/kg/ $?$

Latent heat of evaporation of water, L = 580 cal/g

Mass of the child, m = 30 kg

The heat lost by the child is given as $? θ = m c ? T$ = 30 $\times 1000 \times 1.666$ = 49980 cal

Let $m_{1}$ be the mass of water evaporated from the child’s body in 20 mins.

Loss of heat $? θ$ = $m_{1} \times L$ = 580 $m_{1}$ = $49980 c a l$

$m_{1} =$ 86.2 gm

Rate of evaporation = $\frac{m_{1}}{t}$ = 4.31 g/min

11.17 A ‘thermacole’ icebox is a cheap and an efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side 30 cm has a thickness of 5.0 cm. If 4.0 kg of ice is put in the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45 °C, and co-efficient of thermal conductivity of thermacole is 0.01 J s–1 m–1 K–1. [Heat of fusion of water = 335 × 103 J kg–1]

11.17 Size of the sides of cubical ice box, s = 30 cm =0.3 m

Thickness of the icebox, l = 5 cm = 0.05 m

Mass of ice kept in the box, m = 4 kg

Time gap, t = 6 h = 6 $\times 60 \times 60$ s

Outside temperature, T = 45 °C

Coefficient of thermal conductivity of thermocole, K = 0.01 J $s^{- 1} m^{- 1} K^{- 1}$

Heat of fusion of water, L = 335 $\times 10^{3}$ J ${k g}^{- 1}$

Let m’ be the mass of the ice melts in 6 h

The amount of heat lost by the food: $θ$ = $\frac{K A (T - 0) t}{l}$ , where

A = Surface area of the box = 6 $s^{2}$ = 6 $\times {0.3}^{2} m^{2}$ = 0.54 $m^{2}$

$θ$ = $\frac{0.01 \times 0.54 (45 - 0) \times 6 \times 60 \times 60}{0.05}$ = 104976 J

We also know $θ = m' L$ so m’ = 104976/ (335 $\times 10^{3})$ = 0.313 kg

Hence the amount of ice remains after 6 h = 4 – 0.313 = 3.687 kg

11.18 A brass boiler has a base area of 0.15 m² and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass = 109 J s^–1 m^–1 K^–1 ; Heat of vaporization of water = 2256 × 10³J kg^–1.

11.18 Base area of the boiler, A = 0.15 m2

Thickness of the boiler, l = 1.0 cm = 0.01 m

Boiling rate of water, R = 6.0 kg/min

Let us assume the mass of the boiling water, m = 6 kg and the time to boil, t = 1 min = 60 s

Thermal conductivity of brass, K = 109 J s–1 m–1 K–1

The amount of heat flowing into water through the brass base of the boiler is given by:

$θ$ = $\frac{K A (T_{1} - T_{2}) t}{l}$ , where

$T_{1}$ = Flame temperature in contact with the boiler

$T_{2}$ = Boiling point of water = 100 $?$

Heat required for boiling water $θ$ = mL, where L = heat of vaporization of water = 2256 × 103 J kg–1

By equating for $θ$ we get

6 $\times 2256 \times 10^{3}$ = 109 $\times 0.15 \times (T_{1} - T_{2}) \times 60 / 0.01$

$(T_{1} - T_{2})$ = 137.98 $?$

$T_{1}$ = 237.98 $? (F l a m e t e m p e r a t u r e i n c o n t a c t w i t h t h e b o i l e r)$

11.19 Explain why :

(a) A body with large reflectivity is a poor emitter

(b) A brass tumbler feels much colder than a wooden tray on a chilly day

(c) An optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace

(d) The earth without its atmosphere would be inhospitably cold

(e) Heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water

11.19 (a) A body with a large reflectivity is a bad absorber. A bad absorber will in turn be a poor emitter of radiations.

(b) Brass is a good conductor of heat, when one touches a brass tumbler, heat is conducted from the body to the brass tumbler easily. Hence, the temperature of the body reduces to a colder value and one feels cold.

On the other hand, wood is a poor conductor of heat. Very little heat is conducted from the body to the wooden tray. Resulting in negligible drop in body temperature.

Thus a brass tumbler feels colder than a wooden tray on a chilly day.

(c) Black body radiation equation is given by:

E = $σ$ ( $T^{4}$ - $T_{o}^{4}$ ), where

E = energy radiation

$σ$ = constant

$T =$ temperature of the optical pyrometer

$T_{o}$ = Temperature of open space

$H e n c e a n i n c r e a s e i n t h e t e m p e r a t u r e o f o p e n s p a c e r e d u c e s t h e r a d i a t i o n e n e r g y$

When the same piece of iron placed in a furnace, the radiation energy is E = $σ T^{4}$

(d) In the absence of atmospheric gases, no extra heat will be trapped. All the heat would be radiated back from Earth’s surface.

(e) A heating system based on the circulation of steam is more efficient in warming a building than that based on the circulation of hot water. This is because steam contains surplus heat in the form of latent heat ( 540 cal/g)

11.20 A body cools from 80 °C to 50 °C in 5 minutes. Calculate the time it takes to cool from 60 °C to 30 °C. The temperature of the surroundings is 20 °C.

11.20 According to Newtonâ€™s law of cooling, we have $- \frac{d T}{d t}$
= K(T - $T_{o}$ ) or $\frac{d T}{K (T - T_{o})}$ = -Kdtâ€¦â€¦(i)Where, temperature of the body = T

Temperature of the surroundings = $T_{o}$ = 20 °C

K is a constant

The temperature of the body falls from 80 $?$ to 50 $? i n t i m e t = 5 \min ? = 300 s$

Integrating equation (i), we get

$5080 \frac{d T}{K (T - T_{o})}$ = - $\int_{0}^{300} K d t∫$

$? {[\log_{e} ? (T - T_{o})]}_{30}^{80}$ = -K ${[t]}_{0}^{300}$

$? \frac{2.3026}{K} \log_{10} ? \frac{80 - 20}{50 - 20}$ = -300

$? \frac{2.3026}{300} \log_{10} ? 2$ = K â€¦.(ii)

The temperature of the body falls from 60 $?$ to 30 $? i n t i m e = t'$

Hence, we get:

$\frac{2.3026}{K} \log_{10} ? \frac{60 - 20}{30 - 20}$ = -t'

$? \frac{- 2.3026}{t'} \log_{10} ? 4$ = K....(iii)

Equating equations (ii) and (iii), we get,

$\frac{2.3026}{300} \log_{10} ? 2$ = $\frac{- 2.3026}{t'} \log_{10} ? 4$

$? t^{'} = 300 \times 2 = 600 s$ = 10 min

Hence, the time taken to cool the body from 60 $?$ to 30 $?$ is 10 minutes.

11.21 Answer the following questions based on the P-T phase diagram of carbon dioxide:

(a) At what temperature and pressure can the solid, liquid and vapour phases of CO₂ co-exist in equilibrium ?

(b) What is the effect of decrease of pressure on the fusion and boiling point of CO₂ ?

(c) What are the critical temperature and pressure for CO₂ ? What is their significance?

(d) Is CO₂ solid, liquid or gas at (a) –70 °C under 1 atm, (b) –60 °C under 10 atm 15 °C under 56 atm ?

11.21

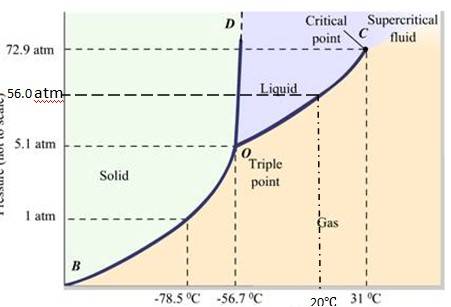
(a) The P-T phase diagram for CO₂is shown here. O is the triple point of the CO₂phase diagram. This means that at the temperature and pressure corresponding to this point, the solid, liquid and vaporous phases of CO₂exists in equilibrium.

(b) The fusion and the boiling points of CO₂decreases with a decrease in pressure.

(c) The critical temperature and critical pressure of CO₂ are 31 $?$ 72.9 atm respectively. Even if it is compressed to a pressure greater than 72.9 atm, CO₂ will not liquefy above the critical temperature.

(d) It can be concluded from the P-T phase diagram of CO2 that:

CO₂ is gaseous at -70 $?$ , under 1 atm pressure.

CO₂ is solid at -60 $?$ , under 10 atm pressure.

CO2 is liquid at 15 $?$ , under 56 atm pressure.

11.22 Answer the following questions based on the P – T phase diagram of CO₂:

(a) CO₂ at 1 atm pressure and temperature – 60 °C is compressed isothermally. Does it go through a liquid phase ?

(b) What happens when CO₂at 4 atm pressure is cooled from room temperature at constant pressure ?

(c) Describe qualitatively the changes in a given mass of solid CO₂ at 10 atm pressure and temperature –65 °C as it is heated up to room temperature at constant pressure.

(d) CO₂ is heated to a temperature 70 °C and compressed isothermally. What changes in its properties do you expect to observe?

11.22

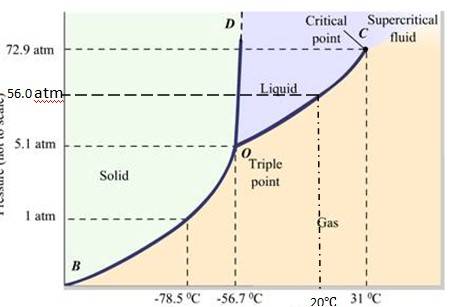
The fusion and boiling points are given by the intersection point where this parallel line cuts the fusion and vaporization curves. It departs from ideal gas behavior as pressure increases.

(a) At 1 atm pressure and at – 60 °C, it lies left of -56.6 $?$ (triple point O). Hence, it lies in the region of vapour and solid phases. Thus, CO₂ condenses into solid state directly, without going through liquid phases.

(b) At 4 atm pressure, CO₂ lies below 5.11 atm (triple point O). Hence it lies in the region of vaporous and solid phases. Thus, CO₂condenses into solid state directly, without going through liquid state.

(c) When the temperature of a mass of solid CO₂ ( at 10 atm pressure and at -65 $?$ is increased, it changes to the liquid phase and then to the vaporous phase. It forms a line parallel to the temperature axis at 10 atm. The fusion and boiling points are given by the intersection point where this parallel line cuts the fusion and vaporization curves.

(d) If CO2 is heated to 70 $?)$ compressed isothermally, then it will not exhibit any transition to the liquid state. This because 70 $? a n d$ is higher than the critical temperature of CO₂. It will remain in the vapour state, but will depart from its ideal behavior as pressure increases.

Explore exams which ask questions on physics ncert solutions class 11th

Select your preferred stream

Engineering

Medicine

Boards

View more exams

physics ncert solutions class 11th Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Popular Courses After 12th

ScienceCommerceArts

Bachelor of Technology (BE/BTech)
Exams accepted
JEE Main | BITSAT | WBJEE
Bachelor of Architecture (BArch)
Exams accepted
NATA | AAT | ITM NEST
Bachelor of Science (BSc)
Exams accepted
CUET | UPCATET | IIT JAM
Bachelor of Computer Applications (BCA)
Exams accepted
BUMAT | GSAT | SET
Bachelor of Medicine & Bachelor of Surgery (MBBS)
Exams accepted
NEET | AYUSH | FMGE

View all courses after 12th

Chartered Accountancy (CA)
Exams accepted
CA Foundation
Company Secretary (CS)
Exams accepted
ICSI Exam
BCom in Accounting & Commerce
Exams accepted
BHU UET | GLAET | GD Goenka Test
Bachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBE
BBA/BMS
Exams accepted
IPMAT | NMIMS - NPAT | SET

View all courses after 12th

BA in Humanities & Social Sciences
Exams accepted
SUAT | JNUEE | BHU UET
Bachelor of Fine Arts (BFA)
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test

View all courses after 12th

News & Updates

Latest NewsPopular News

Class 11 Physics NCERT Solutions Chapter 10 Thermal Properties of Matter (Free PDF)

NCERT Class 11 Physics Chapter 10 Thermal Properties of Matter: Key Topics, Weightage

Class 11 Thermal Properties of Matter Weightage in NEET, JEE Main exam

Try these practice questions

NCERT Physics Class11th Solution PDF for Thermal Properties of Matter

NCERT Physics Class 11th Thermal Properties of Matter Questions and Answers

Commonly asked questions

Explore exams which ask questions on physics ncert solutions class 11th

Student Forum

Other Similar chapters for you

Popular Courses After 12th

News & Updates

SSLC, Plus Two Time Table 2026 Kerala Board Soon; Live Updates on Kerala SSLC, Plus Two Exam Time Table

Gujarat Board Exam Dates 2026 Class 10th, 12th Soon @gseb.org; Live Updates on GSEB SSC, HSC Time Table

JEE Mains Registration 2026 Live: NTA Form Soon at jeemain.nta.nic.in; Notification, Dates, Syllabus

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement