The quantum mechanical model of the atom was proposed by Erwin Schrödinger (through de Broglie's equation). Also, Werner Heisenberg is a key contributing figure.
This modern atomic model describes electrons as wave-like entities that are distributed in a probabilistic manner. It replaced classical orbit-based models.
As we saw while reading about classical atomic models earlier, as well as the developments made until Bohr's model, it's time to move on to the next phase in atomic history.
This article will guide you through de Broglie's hypothesis, Heisenberg's uncertainty principle, Schrödinger's wave equation, quantum numbers, and orbital shapes. All of these are important for understanding the quantum mechanical model of the atom.
Structured for your quick learning needs, and while you prepare for exams, use this comprehensive yet simple guide.
- Quantum Mechanical Model of the Atom: An Introduction
- Features of the Quantum Mechanical Model of the Atom
- Dual Nature of Electrons
- Heisenberg's Uncertainty Principle
- Schrödinger Wave Equation
- Quantum Numbers
- Shapes of Orbitals in Quantum Mechanical Model of an Atom
- Worked Example for Quantum Mechanical Model of the Atom
- Revision Notes for Chemistry Class 11
Quantum Mechanical Model of the Atom: An Introduction
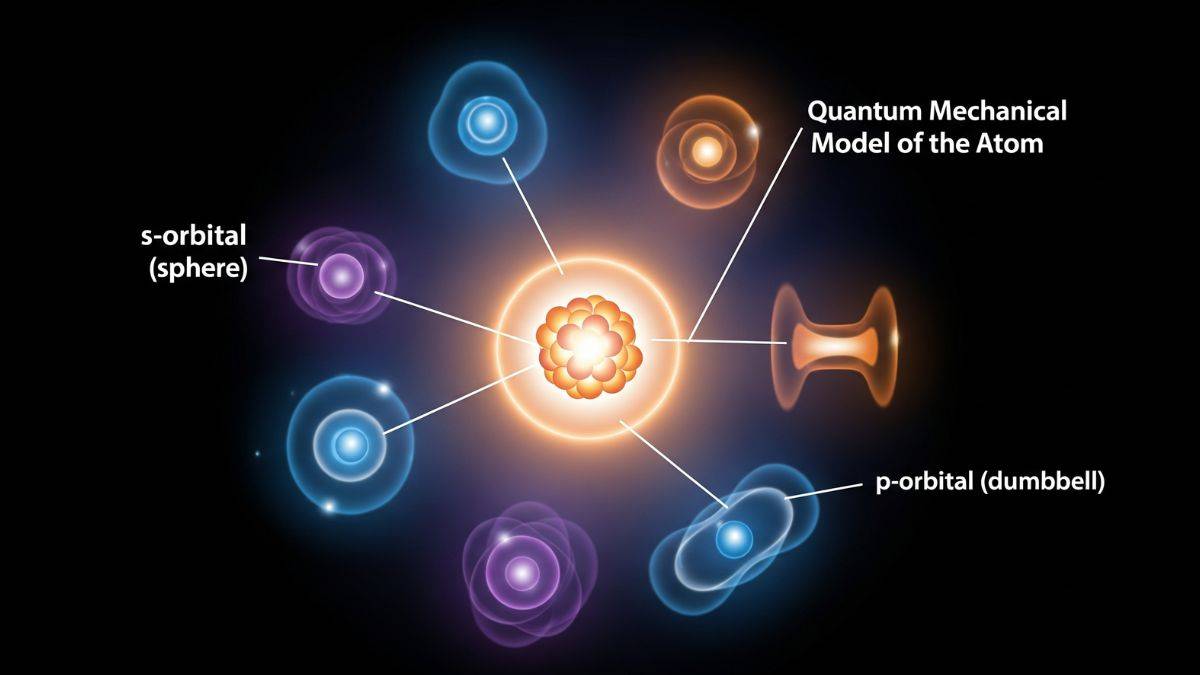
The quantum mechanical model of the atom states that electrons do not move in fixed paths. Instead, they exist in regions, known as orbitals. In these orbitals, there is a greater probability of finding electrons.
There is a lot to unpack here, and from the earlier Chemistry textbook section on Towards the Quantum Mechanical Model of the Atom, you may recall the basics.
In the atomic model of Bohr, his idea of electrons moving like planets in fixed circles around the nucleus (much like the sun) turned out to be wrong. This was especially true for atoms with more than one electron. Experiments showed that electrons don’t follow neat tracks at all. Instead, they hang out in regions of space called orbitals, more like fuzzy clouds where they’re most likely to be found.
De Broglie added to this by suggesting electrons act like waves, and inside the atom, they fit as standing waves around the nucleus.
Heisenberg then showed that it's impossible to find an electron’s position and momentum at the same time. That means exact orbits around the nucleus cannot exist.
Then, Schrödinger created equations that described these orbitals properly. That gave us the modern picture of electrons as probability clouds instead of tidy circles.
In short, this electron behaviour accounts for what we know as quantum mechanics. In the current syllabus of the Chemistry textbook, there is also a brief mention on the difference between classical and quantum mechanics in section 2.6. In case you would want to learn more, see below.
Quantum Mechanics vs. Classical Mechanics
| Feature | Classical Mechanics | Quantum Mechanics |
| What it describes | Bigger or macroscopic stuff we can see. They are stones, cars, planets, etc. | Tiny or microscopic stuff, including electrons, atoms, and molecules. For big objects, it matches classical results |
| Main idea | Newton’s laws. Particles have exact and predictable paths | Matter acts as both waves and particles. Motion is described for objects with this dual behaviour. |
| Electrons | Treated like particles moving in neat and predefined orbits | Treated like waves spread out in clouds. They exist in quantised energy levels. |
| Predictability | You can know both position and speed exactly, so the paths are clear and understood | Follows the Uncertainty Principle. It says that you can’t know position and speed at the same time. Only probabilities exist. |
| Atomic stability | Predicts electrons should crash into the nucleus (so atoms shouldn’t exist) | Explains why atoms are stable and electrons don’t spiral inward. |
| Energy | Continuous, and can take any value | Quantised, only certain 'packets' of energy are allowed |
| Electron distribution | No clear idea about where electrons sit | Electrons exist in orbitals (probability zones) described by wave functions |
| Key equation | No wave equations | Schrödinger’s wave equation defines orbitals and energies |
| Electron spin | Doesn’t explain spin or why it’s quantised | Electrons have spin (up or down). Pauli principle says two electrons in one orbital must spin opposite ways |
| Spectra | Failed to explain atomic line spectra | Explains hydrogen spectrum perfectly and works for multi-electron atoms |
| Limitations | Ignores wave nature of matter, fails for complex atoms | Works, but multi-electron atoms need approximations due to complexity |
Features of the Quantum Mechanical Model of the Atom
In your exams, you may be asked about the features of the atom's quantum mechanical model. Here are the most important ones.
Quantised Energy Levels in Atoms
One of the biggest ideas in the quantum mechanical model is that electrons can only occupy specific energy levels. They can’t just take on any random value. Bohr introduced this concept where he mentions that the electrons' energy is quantised. Like steps on a staircase. This comes from the wave-like behaviour of electrons, which Schrödinger’s wave equation helped explain. Each energy level is tied to the standing wave patterns that electrons can form around the nucleus.
Atomic Orbitals and Electron Probability
Instead of following neat circular orbits like Bohr once imagined, electrons live in regions of space called orbitals. You can think of an orbital as the 'address' of an electron. Each orbital has a set energy and can hold a maximum of two electrons. The shape of these orbitals is based entirely on solutions to Schrödinger’s equation. They could be spherical, dumbbell-shaped, or more complex. We can never know the exact location of an electron at any moment. That's why probability becomes a mathematical way to understand it. And, the square of the wave function, written as |ψ|², tells us the likelihood of finding the electron in a certain spot.
Role of the Uncertainty Principle in Quantum Mechanics
Heisenberg’s Uncertainty Principle mentions we know that we cannot know an electron's exact position and momentum at the same time. Unlike the Bohr model, electrons don’t travel on fixed paths. Instead, they exist as fuzzy clouds of probability. This principle is basic and too important to the quantum mechanical model. It explains why we can only talk about where an electron is likely to be, never exactly where it is.
Dual Nature of Electrons
The dual nature of matter posits that particles, such as electrons, exhibit both particle-like and wave-like properties, with their wavelengths being dependent on their momentum.
(You could further refer to the Law of Conservation of Momentum in Class 11 Physics.)
So, in your Chemistry textbook, you will find out that Louis de Broglie (1924) proposed that electrons, like light, have wave-particle duality, with wavelength given by: where is Planck's constant, is mass, and is velocity. This was verified by Davisson and Germer's electron diffraction experiments.
Mathematical Significance of the Dual Nature of Matter
- For an electron accelerated by a potential :
- In Bohr's orbits, de Broglie's wavelength satisfies:
- Significant for microscopic particles, negligible for macroscopic objects.
Heisenberg's Uncertainty Principle
Heisenberg's Uncertainty Principle states that the position and momentum of a particle cannot be simultaneously measured with exact precision. That introduces an inherent uncertainty in quantum systems.
Werner Heisenberg (1927) formulated: where is position uncertainty, is momentum uncertainty. Similarly, energy and time uncertainty:
This principle limits classical precision in electron measurements. The NCERT Solutions for Chapter 2 Chemistry help you practice numerical problems based on the formula for Heisenberg uncertainty.
Mathematical Significance of the Heisenberg Uncertainty Principle
- Challenges Bohr's fixed orbits, favouring probabilistic electron clouds.
- Impacts spectroscopic and quantum calculations.
JEE problems may test uncertainty calculations or conceptual implications. Have a look at the JEE Main analysis.
Schrödinger Wave Equation
The Schrödinger wave equation describes electrons as three-dimensional waves, with solutions providing probability distributions of electron positions.
Your NCERT textbook mentions that Erwin Schrödinger (1926) proposed:
or
where is the wave function, is total energy, is potential energy, and represents electron probability density.
Key Features of the Schrödinger Equation
- indicates the likelihood of finding an electron, defining atomic orbitals.
- Solutions yield quantum numbers describing electron states.
JEE questions may focus on orbital probability or quantum numbers. Check for such in previous JEE Mains papers.
Quantum Numbers
In general, quantum numbers are integers or half integers that specify an electron's energy, orbital shape, orientation, and spin in an atom.
In Class 11 Chemistry, you learn that there are four quantum numbers which define electron states in the following way.
- Principal Quantum Number ( ): Determines energy and size ( ). Max electrons: .
- Azimuthal Quantum Number ( ): Defines orbital shape ( to ). Subshells: (s), 1 (p), 2 (d), 3 (f). Max electrons: .
- Magnetic Quantum Number : Specifies orbital orientation to . Total values: .
- Electron Spin Number ( ): Indicates electron spin ( or ).
Key Features of Quantum Numbers
- Orbitals are designated as (e.g., ).
- Spin angular momentum: .
JEE problems often involve assigning quantum numbers or calculating electron capacities.
Shapes of Orbitals in Quantum Mechanical Model of an Atom
Orbitals are regions of high electron probability. And, quantum numbers determine their shapes, and that influences chemical bonding.
There are four types of orbital shapes defined in the Structure of Atoms chapter. These are
- s-orbital : Spherical, no nodes for 1 s , radial nodes .
- p-orbital : Dumbbell-shaped, three orientations , one nodal plane.
- d-orbital : Double dumbbell, five orientations (e.g., ), two nodal planes.
- f-orbital : Complex, seven orientations, three nodal planes.
Key Features of Orbitals
- Radial probability: .
- Size increases with .
Worked Example for Quantum Mechanical Model of the Atom
Revision Notes for Chemistry Class 11
Commonly asked questions
How does the quantum mechanical model describe electron location differently from Bohr's?
The quantum mechanical model of the atom is a significant shift from orbits to orbitals. Though Bohr's atomic model was the beginning of understanding of how electrons move in fixed circular paths, it was Heisenberg's Uncertainty Principle that changed the view. It showed exact positions and velocities can't both be known. So definite orbits don't exist.
In the quantum mechanical model of atom, electrons are treated as waves and described by orbitals. These are regions where they are most likely to be found. These come from Schrödinger's wave function, where |? |² gives the probability of locating an electron. Each orbital is defined by three quantum numbers: n (energy level), l (shape), and ml (orientation).
What does the energy of an orbital in a multi electron atom depend on?
In a hydrogen atom, which we know has a single electron, the orbital energy will only depend on the principal quantum number (n). Here, the orbitals like 2s and 2p have the same energy (degenerate).
It's a little different with multielectron atoms. The energy depends on both n and the azimuthal quantum number (l). This causes splitting. And, the energies increase in the order: s < p < d < f.
Chemistry Structure of Atom Exam
Student Forum
Other Topics under this Chapter
- Isotope Meaning
- Mole Concept
- What are Electrons
- Isotopes and Isobars
- What is a Saturated solution
- Difference between Atom and Ion
- Discovery of Sub Atomic Particles
- Atomic Models
- Developments Leading to Bohr's Model of Atom
- Quantum Mechanical Model of Atom
- Bohr's Model of Hydrogen Atom
- Towards Quantum Mechanical Model of Atom
- Structure of Atom
Other Class 11th Chemistry Chapters
- Chemistry Chemical Equilibrium
- Chemistry Structure of Atom
- Chemistry Redox Reactions
- Chemistry Some Basic Concepts of Chemistry
- Chemistry Organic Chemistry
- NCERT Class 11 Chemistry
- Chemistry Classification of Elements and Periodicity in Properties
- Chemistry Chemical Bonding and Molecular Structure
- Chemistry Hydrocarbon
- Chemistry Thermodynamics
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test