Carnot Engine: Class 11 Physics Notes, Definition, Carnot Cycle, Efficiency Derivation & Real-Life Applications

Updated on Jun 10, 2025 19:49 IST

By Syed Aquib Ur Rahman, Assistant Manager

To know the theoretical standard used in making energy conversion efficient in thermodynamics, you have to learn about the Carnot Engine. This hypothetical heat engine, proposed by Sadi Carnot in 1824, establishes the maximum efficiency any engine can achieve when converting heat into work.

We explain the Carnot Engine in detail below to help you ground yourself with the core thermodynamics topics, ranging from the types of thermodynamic processes to the Second Law of Thermodynamics. You can further practice the NCERT Solutions for Thermodynamics.

Table of content

What is Carnot Engine?
Carnot Engine Components
Diagram of Carnot Engine
Carnot Cycle
Carnot Engine Efficiency Derivation and Formula
Second Law of Thermodynamics and Carnot Theorem
Applications of Carnot Engine
JEE Main-Level Examples
Key Points for JEE Main
Common Misconceptions About Carnot Engine to Avoid

What is Carnot Engine?

A Carnot engine is an ideal, reversible heat engine that converts heat into work through a cyclic process between a hot source at a temperature T1( K) and a cold sink at T2 (K). Its efficiency is the maximum possible for any engine operating between these temperatures, given by.

$η = 1 - \frac{T_{2}}{T_{1}}$

NCERT defines it as,“A reversible heat engine operating between two temperatures is called a Carnot engine.”

This NCERT defintion of the Carnot Engine further elaborates that the Carnot Engine has specific conditions and components that enable understanding of how it works in theory.

First, it is essential to consider that the Carnot Engine is an engine that operates between two reservoirs or systems at different temperatures, functioning as a reversible process.

Secondly, this Carnot Engine requires four sequentially paired thermodynamic processes (isothermal and adiabatic) that work as a cycle between the two reservoirs. We explain this more below.

And, before that, check out why you should be learning about the Carnot Engine and related concepts for your engineering entrances.

Importance of Learning About the Carnot Engine for Exams

The Carnot Engine is a direct application of the laws of thermodynamics, and it is applicable to any higher studies you pursue after CBSE Board Exams. Check out the BSc Physics syllabus too.
JEE Mains frequently tests reversibility concepts. The key point is that the Carnot cycle represents a perfectly reversible process; any reversible heat engine operating between identical temperature limits will achieve the same maximum efficiency.

Carnot Engine Components

A reversible process between two reservoirs at different temperatures must have four parts. All these components serve a specific purpose, allowing the engine to return to its initial state while ensuring reversibility and maximum efficiency.

Cylinder

Contains an ideal gas with non-conducting walls and a conducting base.

An ideal gas is required to be in this cylinder, as it acts as the working substance whose behaviour we can predict using the ideal gas equation, PV=nRT.

The cylinder must have non-conducting walls. That prevents side heat transfer, leaving only the base for heat exchange. Additionally, this is only when the process can be truly adiabatic in an isolated scenario.

What happens with a conducting base is that the temperature of the gas remains constant while transferring heat. If you recall from the earlier sections of the chapter, that’s an isothermal process at work.

Source

Infinite thermal capacity at T1, supplying heat Q1.

The source that supplies heat, let’s say, we denote as Q1. It provides the input energy to powers the engine. That causes the gas to expand and do work.

Now, the infinite thermal capacity follows that supplying heat Q1 does not lower the source's temperature. This is important for the first step of the Carnot cycle (isothermal expansion) to occur at a perfectly constant temperature, T1.

Sink

Infinite thermal capacity at T2, absorbing heat Q2.

The sink here becomes the reservoir to absorb waste heat. It has to be ejected from the gas so that the cycle can complete and restart.

So, the absorbing heat Q2 does not raise the sink's temperature. That’s how it reaches the third step (isothermal compression) that remains at a perfectly constant temperature, T2.

Stand

Non-conducting, for adiabatic processes.

This stand is an insulator. It isolates the cylinder from any thermal contact. For both adiabatic expansion and compression stages, this is important. The gas’s temperature changes only when there is work done on it or by it. There is no heat flow.

Diagram of Carnot Engine

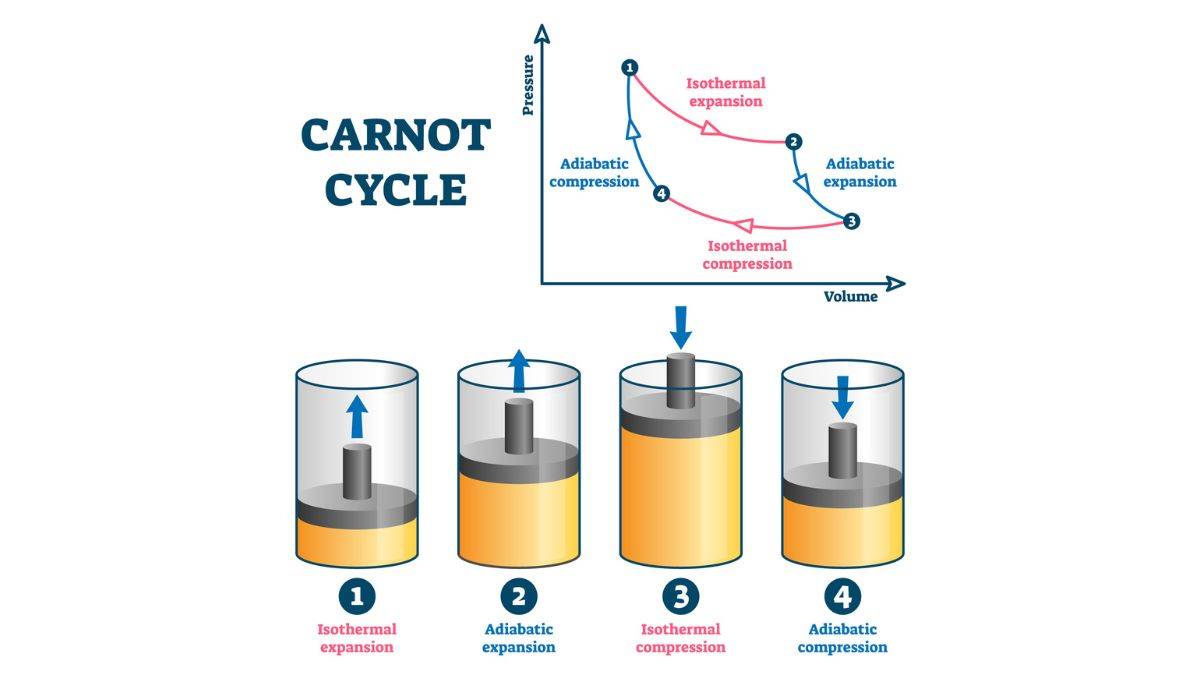
This is the P-V diagram of a Carnot cycle for 1 mol of a monoatomic ideal gas (

γ = 5 / 3

), showing isothermal and adiabatic processes between

T_{1} = 600 K

and

T_{2} = 300 K

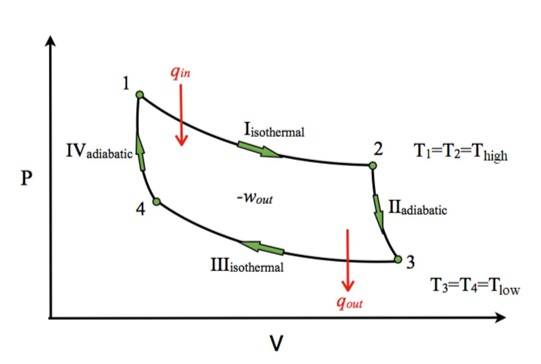
Carnot Cycle

This is the Carnot Cycle in a nutshell. It follows the Carnot Theorem, which states, any system that works between two given temperatures, hot reservoir (T1) and cold reservoir (T2), can never have an efficiency of more than the Carnot engine working between the same reservoirs, respectively.

1. Isothermal Expansion (A to B): Gas expands at $T_{1}$ , absorbing heat $Q_{1}$ . Work done: $W_{1} = R T_{1} l n (\frac{V_{2}}{V_{1}})$ .

2. Adiabatic Expansion (B to C): Gas expands, temperature drops to $T_{2}$ . Work done: $W_{2} = \frac{R (T_{1} - T_{2})}{γ - 1}$ .

3. Isothermal Compression (C to D): Gas is compressed at $T_{2}$ , releasing heat $Q_{2}$ . Work done: $W_{3} = R T_{2} l n (\frac{V_{3}}{V_{4}})$ .

4. Adiabatic Compression ( D to A ): Gas is compressed, temperature rises to $T_{1}$ . Work done: $W_{4} = \frac{R (T_{1} - T_{2})}{γ - 1}$ .

Net work: $W = W_{1} - W_{3}$ , as $W_{2} = W_{4}$ .

Carnot Engine Efficiency Derivation and Formula

Here is the efficiency derivation of the Carnot Cycle.

Efficiency is: $η = \frac{W}{Q_{1}} = \frac{Q_{1} - Q_{2}}{Q_{1}} = 1 - \frac{Q_{2}}{Q_{1}}$

For points B and B on the same adiabatic curve: $T_{1} V_{2}^{γ - 1} = T_{2} V_{3}^{γ - 1} ⟹ \frac{V_{3}}{V_{2}} = {(\frac{T_{1}}{T_{2}})}^{\frac{1}{γ - 1}}$

For points D and C : $T_{1} V_{1}^{γ - 1} = T_{2} V_{4}^{γ - 1} ⟹ \frac{V_{4}}{V_{1}} = {(\frac{T_{1}}{T_{2}})}^{\frac{1}{γ - 1}}$

$\frac{Q_{1}}{T_{1}} = \frac{Q_{2}}{T_{2}} ⟹ \frac{Q_{2}}{Q_{1}} = \frac{T_{2}}{T_{1}}$

Thus, $\frac{V_{3}}{V_{4}} = \frac{V_{2}}{V_{1}}$ , so: $η = 1 - \frac{T_{2}}{T_{1}}$

This shows efficiency depends only on reservoir temperatures.

Second Law of Thermodynamics and Carnot Theorem

In your Physics chapter on Thermodynamics, you get to learn that the Second Law (Clausius and Kelvin-Planck statements) implies no engine can be more efficient than a Carnot engine. Carnot's theorem (page 120) states that all reversible engines between $T_{1}$ and $T_{2}$ have the same efficiency, and no irreversible engine can exceed it.

Applications of Carnot Engine

You might want to figure out the different applications of the Carnot Engine, more particularly where it’s used.

Standard for Efficiency: Real car engines (petrol: $40 %$ , diesel: $50 - 55 %$ ) are compared to Carnot's ideal efficiency.

Refrigeration: The Carnot Cycle can run backwards. It does not convert heat into work. Instead it uses work to move heat from a cold space to a hot space. That functions as an ideal refrigerator.

Thermodynamic Analysis: Used in power plants and HVAC systems.

JEE Main-Level Examples

Here are some important examples of questions that come in JEE Mains.

1. Problem: A Carnot engine operates between $627^{\circ} C$ and $27^{\circ} C$ . Calculate its efficiency. $η = 1 - \frac{T_{2}}{T_{1}} = 1 - \frac{300}{900} = \frac{2}{3} \approx 66$

2. Problem: A Carnot engine takes 1000 J of heat per cycle from a source at 500 K and rejects heat to a sink at 300 K . Find the work done. $η = 1 - \frac{300}{500} = 0.4, W = η Q_{1} = 0.4 \times 1000 = 400$

3. Problem: A Carnot refrigerator operates between $0^{\circ} C$ and $30^{\circ} C$ . Find its coefficient of performance. $β = \frac{T_{2}}{T_{1} - T_{2}} = \frac{273}{303 - 273} = \frac{273}{30} \approx 9.1$