Class 11 Chemistry Equilibrium NCERT Solutions: Chapter 7 Key Topics, Download Questions & Answers PDF

Check all the topics and subtopics that are involved in equilibrium chapter of NCERT class 11 Chemistry subject.

1. Solid-liquid Equilibrium

• Liquid-vapour Equilibrium
• Solid-vapour Equilibrium
• Equilibrium Involving Dissolution of Solid or Gases in Liquids
• General Characteristics of Equilibria Involving Physical Processes

1. Equilibrium in Chemical Processes – Dynamic Equilibrium
2. Law of Chemical Equilibrium and Equilibrium Constant
3. Homogeneous Equilibria

• Equilibrium Constant in Gaseous Systems

1. Heterogeneous Equilibria
2. Applications of Equilibrium Constants

• Predicting the Extent of a Reaction
• Predicting the Direction of the Reaction
• Calculating Equilibrium Concentrations

1. Relationship between Equilibrium Constant K, Reaction Quotient Q and Gibbs Energy G
2. Factors Affecting Equilibria

• Effect of Concentration Change
• Effect of Pressure Change
• Effect of Inert Gas Addition
• Effect of Temperature Change
• Effect of a Catalyst

1. Ionic Equilibrium in Solution
2. Acids, Bases and Salts

• Arrhenius Concept of Acids and Bases
• The Bronsted-lowry Acids and Bases
• Lewis Acids and Bases

1. Ionisation of Acids and Bases

• The Ionisation Constant of Water and Its Ionic Product
• The pH Scale
• Ionisation Constants of Weak Acids
• Ionisation of Weak Bases
• The Relation Between K_aand K_b
• Di- and Polybasic Acids and Di- and Polyacidic Bases
• Factors Affecting Acid Strength
• Common Ion Effect in the Ionisation of Acids and Bases
• Hydrolysis of Salts and the Ph of Their Solutions

1. Buffer Solutions
2. Solubility Equilibria of Sparingly Soluble Salts

• Solubility Product Constant
• Common Ion Effect on Solubility of Ionic Salts

 

Equilibrium Addtional Question

 

7.1. A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.

(a) What is the initial effect of the change on the vapour pressure?

(b) How do the rates of evaporation and condensation change initially?

(c) What happens when equilibrium is restored finally and what will be the final vapour pressure?      
Answer: (a) On increasing the volume of the container, the vapour pressure will initially decrease because the same amount of vapours is now distributed over a larger space.
(b) On increasing the volume of the container, the rate of evaporation will increase initially because now more space is available. Since the amount of the vapours per unit volume decrease on increasing the volume, therefore, the rate of condensation will decrease initially.
(c) Finally, equilibrium will be restored when the rates of the forward and backward processes become equal. However, the vapour pressure will remain unchanged because it depends upon the temperature and not upon the volume of the container.

7.2. What is K_c for the following equilibrium when the equilibrium concentration of each substance is: [SO₂] = 0.60M, [O₂] = 0.82M and [SO₃] = 1.90 M?

2SO₂(g) + O₂(g) ​⇌ 2SO₃(g)                                      

Answer:

K_C​= [SO_3​]² / [SO_2​]²[O₂​]

​     = (1.90)^2​ / (0.60)²(0.82)

     = 12.229 L mol^-1

7.3. At a certain temperature and total pressure of 10⁵Pa, iodine vapour contains 40% by volume of I atoms

I₂ (g) ​⇌ 2I (g)

Calculate K_p for the equilibrium.                                                                    
Answer: According to the given condition,

Total pressure of equilibrium mixture = 10⁵ Pa

Partial pressure of iodine atoms (I), P_I = 40 % of 10⁵ Pa = 0.4 x 10⁵ Pa

Partial pressure of iodine molecules (I₂), P_I2 = 60 % of 10⁵ Pa= 0.6 x 10⁵ Pa

K_p for the equilibrium = (P_I)²/ P_I2 = (0.4 x 10⁵ Pa)² / (0.6 x 10⁵ Pa)= 2.67 x 10⁴ Pa

7.4. Write the expression for the equilibrium constant, Kc for each of the following reactions                                                                                                                   

(i) 2NOCl (g) ​⇌ 2NO (g) + Cl₂ (g)

(ii) 2Cu(NO₃)₂ (s) ​⇌ 2CuO (s) + 4NO₂ (g) + O₂ (g)

(iii) CH₃COOC₂H₅ (aq) + H₂O (l) ​⇌ CH₃COOH (aq) + C₂H₅OH (aq)

(iv) Fe³⁺ (aq) + 3OH^– (aq) ​⇌ Fe(OH)₃(s)

(v) I₂ (s) + 5F₂​⇌2IF₅
Answer: (i) The expression for the equilibrium constant is K_c​= [NO]²[Cl₂​] / [NOCl]²​.
(ii) The expression for the equilibrium constant is K_c​= [NO₂​]⁴[O₂​] / [(2Cu(NO₃)₂]²  = [NO₂​]⁴[O₂​].
(iii) The expression for the equilibrium constant is K_c​= [CH₃​COOH][C₂​H₅​OH] / [CH₃​COOC₂​H₅​]​.
(iv) The expression for the equilibrium constant is K_c​= 1 / [Fe³⁺][OH⁻]³​.
(v) The expression for the equilibrium constant is K_c​= [IF₅​]²​ / [F₂​]⁵.

7.5. Find out the value of K_c for each of the following equilibria from the value of K_p:
(i) 2NOCl (g) ​⇌ 2NO (g) + Cl₂ (g); Kp= 1.8 × 10^–2 at 500 K

(ii) CaCO₃ (s) ​⇌ CaO (s) + CO₂(g); Kp= 167 at 1073 K                                         

Answer: Using the equation K_p = K_c (RT)^Δng

• From the given equation, Δ^ng = 3 – 2 = 1,

R = 0.0821 L atm K^-1 mol^-1

T = 500 K, Kp= 1.8 × 10^–2

Thus, Kc = Kp / (RT)^Δng= (1.8 x 10^-2) / (0.0821 L atm K^-1 mol^-1 x 500 K)

                                       = 4.4 x 10^-4 mol L^-1

• From the given equation, Δ^ng =1,

R = 0.0821 L atm K^-1 mol^-1

T = 1073 K, Kp= 167 atm

Thus, Kc = Kp / (RT)^Δng= (167 atm) / (0.0821 L atm K^-1 mol^-1 x 1073 K)

                                       = 1.9 mol L^-1

7.6. For the following equilibrium, K =6.3 x 10¹⁴ at 1000 K. 

NO (g) + O₃ —–> NO₂ (g) + O₂(g). 

Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is K_c for the reverse reaction?                                             Answer: For reverse reaction, K_C(reverse) = 1/ K_C = 1 / 6.3 x 10¹⁴ = 1.59 x 10^-15

7.7 Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?                                                                                                

Answer:  This is because molar concentration of a pure solid or liquid is independent of the amount present.
Since density as well as molar mass of pure liquid or solid is fixed; their molar concentrations are constant.

The concentration of solid or liquid is =   =   =
At constant temperature, the density and molar mass of pure solid and liquid are constant.
Due to this, their molar concentrations are constant and are not included in the equilibrium constant.

7.8. Reaction between nitrogen and oxygen takes place as follows:
                                                            2N₂​(g) + O₂​(g) ⇌ 2N₂​O(g)
If a mixture of 0.482 mol of N₂ and 0.933 mol of O₂ is placed in a reaction vessel of volume 10 L and allowed to form N₂O at a temperature for which K_c = 2.0 x 10^-37, determine the composition of the equilibrium mixture.                                                                   
Answer:  Let x moles of N₂ (g) take part in the reaction. According to the equation, x/2 moles of O₂ (g) will react to form x moles of N₂O (g). The molar concentration per litre of different species before the reaction and at the equilibrium point is:

	[N2​]	[O2]	[N2​O]
Initial concentration	0.482​/ 10	0.933/ 10	0
Conc. at equilibrium	(0.482 – x) ​/ 10	(0.933 – x/2) / 10	x/ 10

The value of equilibrium constant (2.0 x 10^-37) is extremely small. This means that only small amounts of reactants have reacted. Therefore, value of x is extremely small and can be omitted as far as the reactants are concerned.

Applying Law of chemical equilibrium, Kc = [N_2​O]² / [N₂​]²[O₂]

=>                                                            Kc = 2.0 x 10^-37

               = (x/10)² / [(0.482/ 10)² x (0.933 / 10)²]

           = 0.01 x² / (2.1676 x 10^-4)

       x²= 43.352 x 10^-40

                    x = 6.6 x 10^-20

Therefore,​[N₂​] = 0.0482 mol/L

[O₂] = 0.0933 mol/L

[N_2​O] = 0.1 x x= 0.1 x 6.6 x 10^-20 = = 6.6 x 10^-21 mol/L

7.9. Nitric oxide reacts with Br₂and gives nitrosyl bromide as per reaction given below:

                                                2NO (g) + Br₂ (g) ​⇌ 2NOBr (g)
When 0.087 mole of NO and 0.0437 mole of Br₂ are mixed in a closed container at constant temperature, 0.0518 mole of NOBr is obtained at equilibrium. Determine the compositions of the equilibrium mixture.                                                                                             
Answer: According to the equation, 2 moles of NO (g) react with 1 mole of Br₂ (g) to form 2 moles of NOBr (g). The composition of the equilibrium mixture can be calculated as follows:
No. of moles of NOBr (g) formed at equilibrium = 0.0518 mol
No. of moles of NO (g) taking part in reaction = 0.0518 mol
No. of moles of NO (g) left at equilibrium = 0.087 – 0.0518 = 0.0352 mol
No. of moles of Br₂ (g) taking part in reaction = 1/2 x 0.0518 = 0.0259 mol
No. of moles of Br₂ (g) left at equilibrium = 0.0437 – 0.0259 = 0.0178 mol
The initial molar concentration and equilibrium molar concentration of different species may be represented as:
                                       2NO (g) + Br₂(g) ——————> 2NOBr(g)

	NO	Br2	NOBr
Initial moles	0.087	0.0437	0
Change	-2x	-x	2x
Moles at equilibrium	0.0352	0.0178	0.0518

7.10. At 450 K, Kp = 2.0 × 10¹⁰/bar for the given reaction at equilibrium.

2SO₂(g) + O₂(g) ​⇌ 2SO₃ (g)

What is K_c at this temperature?                                                                             
Answer: Kp = Kc (RT)^∆ng

=>           Kc = Kp (RT)^-∆ng

Putting the values of Kp= 2.0x10¹⁰ bar^-1, R= 0.083 L bar K^-1 mol^-1, T = 450 K, and ∆ng = 2-3= -1

 

=>  Kc = (2.0 x 10¹⁰ bar^-1) x [(0.083 L bar K^-1 mol^-1) x (450 K)]^-(-1)

= 7.47 x 10¹¹ mol^-1 L

= 7.47 x 10¹¹ M^-1

7.11. A sample of HI (g) is placed in a flask at a pressure of 0.2 atm. At equilibrium partial pressure of HI (g) is 0.04 atm. What is K_p for the given equilibrium?

                                    2HI (g) ​⇌ H₂ (g) + I₂ (g)                                                              
Answer: pHI = 0.04 atm, pH₂ = 0.08 atm, pI₂ = 0.08 atm

K_p= (pH₂ x pI₂) / (p_HI)² = (0.08 x 0.08) / (0.04 x 0.04)= 4.0

7.12. A mixture of 1.57 mol of N₂, 1.92 mol of H₂ and 8.13 mol of NH₃ is introduced into a 20 L reaction vessel at 500 K. At this temperature, the equilibrium constant K_c for the reaction

                                    N₂​(g) + 3H_2​ (g) ⇌ 2NH₃​ (g) is 1.7×10²
Is this reaction at equilibrium? If not, what is the direction of net reaction?           
Answer: According to the given equation, concentration quotient,

Qc = [NH₃​]² / [N₂][ H₂]³

     = (8.13/20 mol L^-1)² / (1.57 / 20 mol L^-1) x (1.92 / 20 mol L^-1)³

       = 2.38 x 10³

The equilibrium constant (K_c) for the reaction = 1.7 x 10^-2

As Q_c ≠ K_c, the reaction is not in a state of equilibrium. 

7.13. The equilibrium constant expression for a gas reaction is,
                                                         
Write the balanced chemical equation corresponding to this expression.                
Answer: Balanced chemical equation for the reaction is

                                        4 NO (g) + 6 H₂O (g) ⇋ 4 NH₃ (g) + 5 O₂ (g)

7.14. One mole of H₂O and one mole of CO are taken in a 10 litre vessel and heated to 725 K, at equilibrium point 40 percent of water (by mass) reacts with carbon monoxide according to equation.

                                              H₂O (g) + CO (g) ⇌ H₂ (g) + CO₂ (g)
Calculate the equilibrium constant for the reaction.                                           
Answer: Number of moles of water originally present = 1 mol
Percentage of water reacted= 40%
Number of moles of water reacted= 1 x 40/100 = 0.4 mol
Number of moles of water left= (1 – 0.4) = 0.6 mole

According to the equation, 0.4 mole of water will react with 0.4 mole of carbon monoxide to form 0.4 mole of hydrogen and 0.4 mole of carbon dioxide.
Thus, the molar conc., per litre of the reactants and products before the reaction and at the equilibrium point are as follows:

	H2O	CO	H2	CO2
Initial moles / litre	1/10	1/10	0	0
At Equilibrium	(1 – 0.4) / 10 = 0.6/10	(1 – 0.4) / 10 = 0.6/10	0.4/10	0.4/10

Equilibrium constant, K_c= [H₂][CO₂] / [H₂O][CO]

                                        = [(0.4/10) x (0.4/10)] / [(0.6/10) x (0.6/10)]

                                        = 0.16 / 0.36 = 0.44

7.15. At 700 K, equilibrium constant for the reaction:

H₂​(g) + I₂ (g) ⇌2HI (g)

is 54.8. If 0.5 mol L–1 of HI(g) is present at equilibrium at 700 K, what are the concentration of H₂​(g) and I₂(g) assuming that we initially started with HI(g) and allowed it to reach equilibrium at 700K?                                                                                                  

Answer:

 H₂​(g) + I₂​(g) ⇌ 2HI (g); K=64, T=700K

2HI ⇌ H₂ ​+ I₂; ​K=1/64700K

  a         0      0

a(1−α)   aα/2   aα/2

0.5         x        x

x² / (0.5)²  = 1 / 54.8

x² =   0.25 / 54.8

∴ x =  = 0.068 M

At equilibrium, [H₂] = [I₂] = 0.068 M
7.16. What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of ICl was 0.78 M?                                                       

                                    2ICl (g) ​⇌ I₂ (g) + Cl₂ (g); Kc = 0.14
Answer:

Suppose at equilibrium, the molar concentration of both I₂ and Cl₂ is x mol L^-1.

                                           K_c = [I₂][ Cl₂] / [ICl]²= x² / (0.78 – 2x)²

=>                     x/ (0.78 – 2x) = (0.14)^1/2 = 0.374

=>                                          x= 0.167

                [ICl] = (0.78 – 2 x 0.167) = (0.78 – 0.334) = 0.446 M

      [I₂] = 0.167 M,

    [Cl₂] = 0.167 M

7.17. K_p =0.04 atm at 898 K for the equilibrium shown below. What is the equilibrium concentration ok C₂H₆ when it is placed in a flask at 4 atm pressure,and allowed to come to equilibrium.

                                                 C_2​H₆​(g) ⇌ C₂​H₄​(g) + H₂​(g).                                    
Answer: The equilibrium reaction is

                  C_2​H₆​(g) ⇌ C₂​H₄​(g)+H₂​(g).

Initial	4	0	0
Change	−x	x	x
Equilibrium	4−x	x	x

The expression for the equilibrium constant is Kp​= (​​P_C2​H4​​) (P_H2) / P_{C2​H6​​​.}
Substituting the values in the above equation, we get
                        0.04=x² / (4−x)

​ or                         x=0.38
Thus, the pressure of ethane is, P_C2​H6​​=3.62atm.

7.18. Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:

                        CH₃COOH (l) + C₂H₅OH (l) ​⇌CH₃COOC₂H₅ (l) + H₂O (l)

(i) Write the concentration ratio (reaction quotient), Qc, for this reaction (note: water is not in excess and is not a solvent in this reaction)

(ii) At 293 K, if one starts with 1.00 mol of acetic acid and 0.18 mol of ethanol, there is 0.171 mol of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.

(iii) Starting with 0.5 mol of ethanol and 1.0 mol of acetic acid and maintaining it at 293 K, 0.214 mol of ethyl acetate is found after sometime. Has equilibrium been reached?   Answer:

• The concentration ratio (Concentration quotient), Qc for the reaction is:

Q_c = [CH₃COOC₂H₅][ H₂O] / [CH₃COOH] [C₂H₅OH]

•  

	CH3COOH	C2H5OH	CH3COOC2H5	H2O
Initial molar concentration	1.0 mol	0.18 mol	0	0
Molar concentration at equilibrium	(1 – 0.171) = 0.829 mol	(0.18 – 0.171) = 0.009 mol	0.171 mol	0.171 mol

Applying

K_c = [CH₃COOC₂H₅][H₂O] / [CH₃COOH] [C₂H₅OH]

     = (0.171 mol) x (0.171 mol) / (0.829 mol) (0.009 mol)

     = 3.92

(iii)

	CH3COOH	C2H5OH	CH3COOC2H5	H2O
Initial molar concentration	1.0 mol	0.5 mol	0.214 mol	0.214 mol
Molar concentration at equilibrium	(1 – 0.214) = 0.786 mol	(0.5 – 0.214) = 0.286 mol	0.214 mol	0.214 mol

Q_c = [CH₃COOC₂H₅][H₂O] / [CH₃COOH] [C₂H₅OH]

     = (0.214 mol) x (0.214 mol) / (0.786 mol) (0.286 mol)

     = 0.204

Since Q_c is less than K_c, this means that the equilibrium has not been reached. The reactants are still taking part in the reaction to form the products.

7.19. A sample of pure PCl₅ was introduced into an evacuated vessel at 473 K. After equilibrium was reached, the concentration of PCl₅ was found to be 0.5 x 10^-1 mol L^-1. If K_c is 8.3 x 10^-3 what are the concentrations of PCl₃ and Cl₂ at equilibrium?
Answer: Let the initial molar concentration of PCl₅ per litre = x mol
Molar concentration of PCl₅ at equilibrium = 0.05 mol
Therefore, moles of PCl₅ decomposed = (x – 0.05) mol
Moles of PCl₃ formed = (x – 0.05) mol
Moles of Cl₂ formed = (x – 0.05) mol
The molar conc./litre of reactants and products before the reaction and at the equilibrium point are:

	PCl5	PCl3	Cl2
Initial moles/litre	x	0	0
At equilibrium	0.05	x – 0.05	x – 0.05

 

                 K_c = [PCl₃][Cl₂] / [PCl₅]

=>8.3 x 10^-3 = (x – 0.05)² / 0.05

=> (x – 0.05) = (4.15 x 10^-4)^1/2 = 2.037 x 10^-2 = 0.02 moles

=>               x = 0.05 + 0.02 = 0.07 mol

Therefore, at equilibrium:

Moles of PCl₃ formed = (x – 0.05) mol = 0.07 – 0.05 = 0.02 mol
Moles of Cl₂ formed = (x – 0.05) mol = 0.07 – 0.05 = 0.02 mol

7.20. One of the reactions that takes place in producing steel from iron ore is the reduction of iron (II) oxide by carbon monoxide to give iron metal and CO2.

                        FeO (s) + CO (g) Fe (s) + CO₂ (g); K_p = 0.265 atm at 1050K

What are the equilibrium partial pressures of CO and CO₂ at 1050 K if the initial partial pressures are: p_CO= 1.4 atm and p_CO2= 0.80 atm?                                  Answer: The initial partial pressures of CO and CO₂​ are 1.40 atm and 0.8. atm respectively.
The expression for the reaction quotient is:
                        Q_p​=​P_CO2 / P_CO​​​=0.80 / 1.4 ​= 0.571
As the value of the reaction quotient is greater than the value of the equilibrium constant, the reaction will move in the backward direction.
To attain the equilibrium, the partial pressure of CO₂ ​will decrease and the partial pressure of CO will increase.
Let p atm be the decrease in the partial pressure of CO₂​. The increase in the partial pressure of CO will be p atm.
The equilibrium partial pressure of CO₂​ is (0.80 – p) atm.
The equilibrium partial pressure of CO is (1.4 + p) atm.
The equilibrium constant is: 
                  K_p ​= ​P_CO2 / P_CO= (0.80−p) / (1.4 + p) ​=0.265
 0.265(1.4+p) = (0.80 – p)
0.371+0.265p = (0.80 – p)
                      p= 0.339 atm
The equilibrium partial pressure of CO is 1.4+0.339= 1.739.
The equilibrium partial pressure of CO₂​ is 0.80−0.339= 0.461 atm.

 7.21 Equilibrium constant, Kc for the reaction

                        N₂ (g) + 3H₂ (g) ​⇌ 2NH₃ (g) at 500 K_c is 0.061

At a particular time, the analysis shows that composition of the reaction mixture is 3.0 mol L^–1 N₂, 2.0 mol L^–1 H₂ and 0.5 mol L^–1 NH₃. Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?                     

Answer: According to available data:

N₂ = [3.0], H₂ = [2.0], NH₃ = [0.50]

Q_c = [NH₃]² / [N₂][ H₂]³

     = [0.50]² / [3.0][ 2.0]³

     = 0.25/24

     = 0.0104.

Since the value of Q_c is less than that of K_c (0.061), the reaction is not in a state of equilibrium. It will proceed in the forward direction till Q_c becomes the same as K_c.

7.22. Bromine monochloride (BrCl) decomposes into bromine and chlorine and reaches the equilibrium:
2BrCl (g) ​⇌ Br₂ (g) + Cl₂ (g)
The value of Kc is 32 at 500 K. If initially pure B_rCl is present at a concentration of 3.3 x10^-3mol L^-1, what is its molar concentration in the mixture at equilibrium?   Answer:  Let x moles of BrCl decompose in order to attain the equilibrium. The initial molar concentration and the molar concentration at equilibrium point of different species may be represented as follows:
2BrCl₂​(g) ​→​Ar_2​(g)+Cl₂​(g)

3.3×10⁻³m        0             0

3.3×10⁻³−2αα​             α

∴ Kc​= (α×α)​ /(3.3×10−3−2α)²

⇒ α² / (3.3×10−3−2α)²​=32

⇒ α / (3.3×10−3−2α)^2​=4

⇒ α=18.67×10−3−8 α

⇒ (1+ 8 α =18.67×10⁻³

⇒ α= 1.5162×10⁻³

∴ Molar concentration of BrCl at equation 

[BrCl] =3.3×10⁻³−2α

=3.3×10⁻³−2×1.562×10⁻³

=0.267×10⁻³M

 7.23. At 1127 K and 1 atm pressure, a gaseous mixture of CO and CO₂ in equilibrium with solid carbon has 90.55% CO by mass.

                                                            C (s) + CO₂ (g) ​⇌ 2CO (g)

Calculate K_c for this reaction at the above temperature.                                      
Answer: Let the mixture has 100g as total mass.
So, The masses of CO and CO₂​ are 90.55g and 100 − 90.55 = 9.45 g respectively.
Therefore, te number of moles of CO

                        n= 90.55 / 28 ​= 3.234.
The number of moles of CO₂​ 

                        n= 9.45 / 44 ​= 0.215.
The mole fraction of CO

                         = 3.234​ / (3.234+0.215) =0.938.
The mole fraction of CO₂​  

                         = 1−0.938=0.062.
The partial pressure of CO is the product of the mole fraction of CO and the total pressure.
It is 0.938×1=0.938 atm.
The partial pressure of carbon dioxide is 0.062×1=0.042 atm.
The expression for the equilibrium constant is: 
K_p​=​​ (P_CO)² / (P_CO2) ​​=(0.938)² / (0.062) ​=14.19
Δn_g​= 2−1=1
K_c​= K_p​(RT)^−Δn=14.19×(0.0821×1127)⁻¹= 0.153.

 7.24. Calculate (a) ∆G^ϴ and (b) the equilibrium constant for the formation of NO₂ from NO and O₂ at 298 K

NO (g) + ½ O₂ (g)​⇌ NO₂ (g)

where

Δ_fG^ϴ (NO2) = 52.0 kJ/mol

Δ_fG^ϴ (NO) = 87.0 kJ/mol

Δ_fG^ϴ (O2) = 0 kJ/mol                                                                                               
Answer:(a) ΔG^ϴ = Δ_f​G^ϴ(NO₂​) − [Δ_f​G^ϴ(NO) + ½ ​Δ_f​G^ϴ(O₂​)]

    = 52.0 − 87.0 −1/2 × 0

                            = −35 kJ/mol
(b) logK = − ΔG^ϴ / 2.303RT = − 35×10³ / (2.303 × 8.314 × 298) ​

               = 6.314
           K = antilog (6.314)

               = 1.362 × 10⁶

7.25. Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?                                                                                                                     

(a) PCl₅ (g) ​⇌ PCl₃ (g) + Cl₂ (g)

(b) CaO (s) + CO₂ (g) ​⇌ CaCO₃ (s)

(c) 3Fe (s) + 4H₂O (g) ​⇌ Fe₃O₄ (s) + 4H₂ (g)

Answer: (i) Pressure will increase in the forward reaction and number of moles of products will increase.
(ii) Pressure will increase in backward reaction and number of moles of products will decrease.
(iii) The change in pressure will have no effect on the equilibrium constant and there will be no change in the number of moles.

7.26. Which of the following reactions will get affected by increasing the pressure? Also mention whether the change will cause the reaction to go into forward or backward direction.

(i) COCl₂ (g) ​⇌ CO (g) + Cl₂ (g)

(ii) CH₄ (g) + 2S₂ (g) ​⇌ CS₂ (g) + 2H₂S (g)

(iii) CO₂ (g) + C (s) ​⇌ 2CO (g)

(iv) 2H₂ (g) + CO (g) ​⇌ CH₃OH (g)

(v) CaCO₃ (s) ​⇌CaO (s) + CO₂ (g)

(vi) 4NH₃ (g) + 5O₂ (g) ​⇌ 4NO (g) + 6H₂O (g)
Answer:  Only those reactions will be affected by increasing the pressure in which the number of moles of the gaseous reactants and products are different (i.e. when n_p ≠ n_r) (gaseous). In general,

• The reaction will go to the left if n_p> n_r.
• The reaction will go to the right if n_r> n_p.
  Keeping this in mind,

(i) Increase in pressure will favour backward reaction because n_p (2) > n_r (1)
(ii) Increase in pressure will not affect equilibrium because n_p = n_r = 3.
(iii) Increase in pressure will favour backward reaction because n_p (2) > n_r (1)
(iv) Increase in pressure will favour forward reaction because n_p (1) < n_r (2)
(v) Increase in pressure will favour backward reaction because n_p (1) > n_r (0).

(vi) Increase in pressure will favour backward reaction because n_p (10) > n_r (9).

7.27. The equilibrium constant for the following reaction is 1.6 ×10⁵ at 1024K

                                                H₂(g) + Br₂(g) ​⇌ 2HBr(g)

Find the equilibrium pressure of all gases if 10.0 bar of HBr is introduced into a sealed container at 1024K.                                                                                                         
Answer: For the equilibrium reaction

                            2HBr (g) ⇌ H₂(g) + Br₂(g) , the equilibrium constant is K = 1/1.6×10⁵.

Initial pressure     10               0           0

At equilibrium      10-p          p/2        p/2

The equilibrium constant expression is
            K_p=P_H2P_Br2 / (P_HBr)²=(p/2)×(p/2) / (10−p)²=1 / 1.6×10⁵
            p² / 4(10−p)²=1 / 1.6×10⁵
                        400p= 20−2p

                              p= 0.0498 bar

The equilibrium pressures are
P_H2=P_Br2=0.0498 / 2=0.0249 bar
P_HBr=10−0.0498=10 bar

7.28 Dihydrogen gas is obtained from natural gas by partial oxidation with steam as

per following endothermic reaction:

                                                CH₄ (g) + H₂O (g) ​⇌ CO (g) + 3H₂ (g)

(a) Write as expression for Kp for the above reaction.

(b) How will the values of Kp and composition of equilibrium mixture be affected by

(i) increasing the pressure

(ii) increasing the temperature

(iii) using a catalyst?  
Answer: (a) The expression for K_p for the reaction is:

                                    Kp = (pCO) x (pH₂) / (pCH₄) x (pH₂O)
(b) (i) By increasing the pressure, the number of moles per unit volume will increase. In order to decrease the same, the equilibrium gets shifted to the left or in the backward direction. As a result, more of reactants will be formed and the value of K_p will decrease.
(ii) If the temperature is increased, according to Le Chatelier’s principle, the forward reaction will be favoured as it is endothermic. Therefore, the equilibrium gets shifted to the right and the value of K_p will increase.
(iii) The addition of catalyst will not change the equilibrium since it influences both the forward and the backward reactions to the same extent. But it will be attained more quickly.

7.29. Describe the effect of:
(i) addition of H₂ (ii) addition of CH₃OH
(iii) removal of CO (iv) removal of CH₃OH

on the equilibrium of the reaction:

2H₂(g) + CO (g) ​⇌ CH₃OH (g)   
Answer: (i) Equilibrium will be shifted in the forward direction.
(ii) Equilibrium will be shifted in the backward direction.
(iii) Equilibrium will be shifted in the backward direction.
(iv) Equilibrium will be shifted in the forward direction.

7.30. At 473 K, the equilibrium constant K_c for the decomposition of phosphorus pentachloride (PCl₅) is 8.3 x 10^-3. If decomposition proceeds as:
PCl₅ (g) ​⇌ PCl₃ (g) + Cl₂ (g) ΔrH^ϴ = 124.0 kJ mol^–1
(a) Write an expression for K_c for the reaction
(b) What is the value of K_c for the reverse reaction at the same temperature.
(c) What would be the effect on K_c if
(i) More of PCl₅is added (ii) pressure is increased (iii) the temperature is increased.  

Answer: (a) The equilibrium constant expression is
           Kc​ = [PCl3​][Cl2​]​ / [PCl5​]
(b) The equilibrium constant expression for the reverse reaction is
          K_c​(reverse) = 1/(8.3×10⁻³) ​=120.48
(c) (i) By adding more of PCl₅, value of K_c will remain constant because there is no change in temperature.
(ii) When pressure is increased, the value of the equilibrium constant remains unaffected.

(iii) By increasing the temperature, the forward reaction will be favoured since it is endothermic in nature. Therefore, the value of equilibrium constant will increase.

7.31. Dihydrogen gas used in Haber’s process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of CO and H₂ In second stage, CO formed in first stage is reacted with more steam in water gas shift reaction.

                                                CO (g) + H₂​O(g) ⇌ CO₂​(g) + H₂​(g)
If a reaction vessel at 400°C is charged with an equimolar mixture of CO and steam so that P_CO = P_H2O = 4.0 bar, what will be the partial pressure of H₂ at equilibrium? K_p = 10.1 at 400°C.                                                                                                                       
Answer: Let the partial pressures of CO and H₂ be p.

                                    CO (g) + H₂​O(g) ⇌ CO₂​(g) + H₂​(g)

Initial conc.                 4 bar       4 bar             0          0

At equilibrium            4-p          4-p                p          p

.
The expression for the equilibrium constant is
K_p​ = ​P_CO2 ​​P_H2​​​ / P_CO​P_H2​O

     = (p×p) / (4−p)(4−p) ​= 10.1
  p = 12.712- 3.17p
  p = 3.04 bar.

7.32. Predict which of the following will have appreciable concentration of reactants and products:                                                                                                                    

1. a) Cl₂ (g) ​⇌2Cl (g) K_c = 5 ×10^–39
2. b) Cl₂ (g) + 2NO (g) ​⇌2NOCl (g) K_c = 3.7 × 10⁸
3. c) Cl₂ (g) + 2NO2 (g) ​⇌2NO₂Cl (g) K_c = 1.8
   Answer: Following conclusions can be drawn from the values of K_c.
   (a) Since the value of K_c is very small, this means that the molar concentration of the products is very small as compared to that of the reactants.
   (b) Since the value of K_c is quite large, this means that the molar concentration of the products is very large as compared to that of the reactants.
   (c) Since the value of K_c is 1.8, this means that both the products and reactants have appreciable concentration.

 

7.33. The value of K_c for the reaction 3O₂(g) ​⇌2O₃(g) is 2.0 x 10^-50 at 25°C. If equilibrium concentration of O₂ in air at 25°C is 1.6 x 10^-2, what is the concentration of O₃?
Answer: The equilibrium constant expression is 
                                    K_c​ = [O₃​]² /[O₂​]³​
                        2.0×10⁻⁵⁰ = [O₃​]² /(1.6×10⁻²)³​
                                [O_3​]²=2.0×10⁻⁵⁰×(1.6×10⁻²)³

     =8.192×10⁻⁵⁶

Hence, the equilibrium concentration of ozone is
                                [O_3​]= 2.86×10⁻²⁸M

7.34. The reaction, CO(g) + 3H₂(g) ​⇌ CH₄(g) + H₂O(g) is at equilibrium at 1300 K in a 1L flask. It also contains 0.30 mol of CO, 0.10 mol of H₂ and 0.02 mol of H₂O and an unknown amount of CH₄ in the flask. Determine the concentration of CH₄ in the mixture. The equilibrium constant, K_c for the reaction at the given temperature is 3.90.            
Answer: 

                                 K_c = [CH₄] [H₂O] / [CO][H₂]³
                                 3.90 = [CH₄]×0.02 / (0.30)(0.10)³
                              [CH₄] = 3.90×0.30×(0.10)³ / 0.02

    =5.85×10⁻² M

Thus, the concentration of methane in the mixture is 5.85×10⁻² M.

 7.35. What is meant by conjugate acid-base pair? Find the conjugate acid/base for the following species: HNO₂, CN^–, HClO₄F^–, OH^–, CO₃^2-, and S^2-.                      Answer: An acid-base pair which differs by a proton only is known as conjugate acid-base pair. For example, HCl, and Cl⁻ represents conjugate acid base pair.

The conjugate acid/base for the species HNO₂, CN^–, HClO₄F^–, OH^–, CO₃^2-, and S^2- are NO₂^–, HCN, ClO₄^–, HF, H₂O, HCO₃^– and HS^–.respectively.

7.36. Which of the following are Lewis Acids?
                                   H₂O,BF₃, H⁺ and NH⁴⁺                                                                                            
Answer:  BF₃, H⁺ ions are Lewis acids.

7.37. What will be the conjugate bases for the Bronsted acids: HF, H₂SO₄ and H₂CO₃?   

Answer:  Conjugate bases: F^–, HSO^–₄ , HCO^–₃.

7.38. Write the conjugate acids for the following Bronsted bases:
NH₂, NH₃ and HCOO^–                                                                                                                                                  
Answer: NH₃, NH₄⁺ and HCOOH

7.39. The species H₂O, HCO₃^–, HSO₄^– and NH₃ can act both as Bronsted acid and base. For each case, give the corresponding conjugate acid and base.             Answer:

 

7.40. Classify the following species into Lewis acids and Lewis bases and show how these can act as Lewis acid/Lewis base?
(a) OH^–  (b) F^– (c) H⁺ (d) BCl₃                                                                                        
Answer:  (a) OH^– ions can donate an electron pair and act as Lewis base.
(b) F^– ions can donate an electron pair and actas Lewis base.
(c) H⁺ ions can accept an electron pair and act as Lewis acid.
(d) BCl₃ can accept an electron pair since Boron atom is electron deficient. It is a Lewis acid.

7.41. The concentration of hydrogen ions in a sample of soft drink is 3.8 x 10^-3 M. What is the pH value?                                                                                         Answer:  pH = – log [H⁺] = – log (3.8 x 10^-3) = – log 3.8 + 3 = 3 – 0.5798 = 2.4202 = 2.42

7.42. The pH of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it.                                                                                                              Answer: pH = – log [H⁺] or log [H⁺] = – pH = – 3.76 = 4.24
Therefore, [H⁺] = Antilog 4.24 = 1.738 x 10^-4 = 1.74 x 10-4 M

7.43. The ionization constant of HF, HCOOH and HCN at 298 K are is 6.8 x 10^-4, 1.8x 10^-4 and 4.8 x 10^-9 respectively, calculate the ionization constant of the corresponding conjugate base. 

Answer: For F^–, K_b =K_w/K_a= 10^-14/(6.8 x 10^-4)

                     = 1.47 x 10^-11 = 1.5 x 10^-11 .
       For HCOO-, K_b = 10^-14/(1.8 x 10^-4)

                     = 5.6 x 10^-11 
             For CN^–, K_b= 10^-14/(4.8 X 10^-9)

                    = 2.08 x 10^-6

7.44. The ionization constant of phenol is 1.0 x 10^-10. What is the concentration of phenolate ion in 0.05 M solution of phenol? What will be its degree of ionization if the solution is also 0.01 M in sodium phenolate?                                                                            
Answer:                                              C₆H₅OH ​⇌ C₆H₅O^- + H⁺

	C6H5OH	C6H5O-	H+
Initial	0.05 M	0	0
After dissociation	0.05 –x	x	x

K_a = x² / (0.05 - x) = 1.0 x 10^-10

=> x² / 0.05 = 1.0 x 10^-10

=>           x² = 5 x 10^-12

=>             x= 2.2 x 10^-6 M

In presence of 0.01 C₆H₅Na, suppose y is the amount of phenol dissociated, then at equilibrium

[C₆H₅OH] = 0.05 – y ≈ 0.05,

  [C₆H₅O^-] = 0.01 + y ≈ 0.01 M, [H⁺] = yM

Therefore, Ka = (0.01) (y) / (0.05) = 1.0 x 10^-10

 =>               y = 5 x 10^-10

And             α = y/c = (5 x 10^-10) / (5 x 10^-2)

           = 10^-8

7.45. The-first ionization constant of H₂S is 9.1 x 10^-8. Calculate the concentration of HS^– ions in its 0.1 M solution and how will this concentration be affected if the solution is 0.1 M in HCl also? If the second dissociation constant of H₂S is 1.2 x 10^--13, calculate the concentration of S^2-under both conditions.                     Answer:(i) To calculate [HS⁻] in absence of HCl:
Let, [HS⁻] = x M.
                                                            H_2​S ⇌ H⁺ + HS⁻
The initial concentrations of H_2​S, H⁺ and HS⁻ are 0.1 M, 0 M and 0 M respectively.
Their final concentrations are 0.1-x M, x M and x M respectively.
            K_a​ = [H₂​S][H⁺][HS⁻]​
  9.1×10⁻⁸ = x × x / (0.1−x)​
In the denominator, 0.1-x can be approximated to 0.1 as x is very small.
   9.1×10⁻⁸=x×x / (0.1)​
                x=9.54×10⁻⁵M= [HS⁻]

(ii) To calculate [HS⁻] in presence of HCl:
Let [HS⁻]= y M.
                                                            H₂​S⇌H⁺+HS⁻
The initial concentrations of H_2​S,H⁺ and HS⁻ are 0.1 M, 0 M and 0 M respectively.
Their final concentrations are 0.1-y M, y M and y M respectively.
Also,                                                    HCl⇌H⁺+Cl⁻
For HCl [H⁺]=[Cl⁻]=0.1M
K_a​= [HS⁻][H⁺] / [H_2​S]​
K_a​= y(0.1+y)​ / (0.1−y)
In the denominator, 0.1-y can be approximated to 0.1 and in the numerator, 0.1+y can be approximated to 0.1 as y is very small.
9.1×10⁻⁸= (y×0.1) / 0.1​
            y= 9.1×10⁻⁸M= [HS⁻]

 

(iii) To calculate [S²⁻] in absence of 0.1 M HCl:
                                                                        HS⁻⇌H⁺+S²⁻
[HS⁻]=9.54×10⁻⁵M
Let [S²⁻]= x M.
[H⁺]= 9.54×10⁻⁵ M
                  K_a​= [H⁺][S²⁻]​ / [HS⁻]
= >1.2×10⁻¹³= (9.54×10⁻⁵×X​) / (9.54×10⁻⁵)
= >              x=1.2×10⁻¹³M= [S²⁻]

 

(iv) To calculate [S²⁻] in presence of 0.1 M HCl:
Let [S²⁻]= x′ M.
[HS⁻]= 9.1×10⁻⁸ M
[H⁺]= 0.1 M (from HCl)
            K_a​= [HS⁻][H⁺][S²⁻]​
1.2×10⁻¹³= (0.1×X′​) / (9.1×10⁻⁸)
              x′= 1.092×10⁻¹⁹= [S²⁻]

7.46. The ionization constant of acetic acid is 1.74 x 10^-5. Calculate the degree of dissociation of acetic acid in its 0.05 M solution. Calculate the concentration of acetate ion in the solution and its pH.                                                                                                                                   
Answer:

The dissociation equilibrium is 

CH_3​COOH ⇌ CH3​COO⁻ + H⁺.
Let α be the degree of dissociation.
The equilibrium concentrations of CH_3​COOH,CH₃COO⁻ and H⁺ are c(1−α),c(α) and c(α) respectively.
The equilibrium constant expression is K_c​= [CH_3​COO⁻][H⁺]​ / [CH₃​COOH].

 K_c​=(cα)(cα) / c(1−α) ​≈cα²
= (K_a​ / c)^1/2​​=(1.74×10⁻⁵ / 0.05)^1/2​​

=1.865×10⁻²
[CH3​CO⁻]= [H⁺]= cα= 0.05×1.865×10⁻²= 9.33×10⁻⁴M
pH= −log[H⁺]= −log(9.33×10⁻⁴)= 3.03

The concentration of acetate ion and its pH are 9.33×10⁻⁴ and 3.03 respectively.

7.47. It has been found that the pH of a 0.01 M solution of an organic acid is 4.15. Calculate the concentration of the anion, the ionization constant of the acid and its PK_a.
Answer: pH= −log[H⁺]=4.15

[H⁺]= antilog(−4.15)= 7.08×10⁻⁵

[A⁻]=[H⁺]=7.08×10⁻⁵

The concentration of undissociated acid is 0.01−0.000071=0.009929M.

                                                HA+H₂​O⇌H₃​O⁺+A⁻

K_a​= [H₃​O⁺][A⁻] / [HA] ​= (7.08×10⁻⁵)(7.08×10⁻⁵)​ / 0.009929

    = 5.05×10⁻⁷

pK_a​= −logK_a​= −log5.05×10⁻⁷ ≈ 6.3

 7.48. Assuming complete dissociation, calculate the pH of the following solutions:
(a) 0.003 M HCl (b) 0.005 M NaOH (c) 0.002 M HBr (d) 0.002 M KOH.              
Answer: (a) 0.003 M HCl
[H_3​O⁺] = [HCl] = 0.003M
       pH = −log[H⁺] = −log(3.0×10⁻³) = 2.523

(b) 0.005 M NaOH
[OH⁻] = [NaOH] = 0.005M
   [H⁺] = K_w​ / [OH⁻] ​= 10⁻¹⁴/ 0.005​=2×10⁻¹²
      pH= −log[H⁺]=−log(2×10⁻¹²)=11.699

(c) 0.002M HBr
[H⁺]= [HBr]=0.002
   pH= −log[H⁺]=−log0.002=2.699

(d)0.002M KOH
[OH⁻]=[KOH]=0.002M
    [H⁺]= Kw / [OH⁻] ​=10⁻¹⁴ / 0.002 ​=5×10⁻¹²
       pH= −log[H⁺]=−log(5×10⁻¹²)=11.301

7.49. Calculate the pH of the following solutions:
(a) 2g ofTlOH dissolved in water to give 2 litre of the solution
(b) 0.3 g of Ca(OH)₂ dissolved in water to give 500 mL of the solution
(c) 0.3 g of NaOH dissolved in water to give 200 mL of the solution
(d) l mL of 13.6 M HCl is diluted with water to give 1 litre of the solution.   

Answer: (a) For 2g of TlOH dissolved in water to give 2 L of solution:

[TlOH] = [OH⁻] = (2×1)​ / (2×221) = (1 / 221)​M
    pOH = −log[OH]⁻ = −log(1/221) ​

             = 2.35
       pH = 14 – pOH = 14 − 2.35 = 11.65

(b) For 0.3 g of Ca(OH)2​ dissolved in water to give 500 mL of solution:

[OH⁻] = 2[Ca(OH)₂​] = 2(0.3×1000/500​) = 1.2M
  pOH = −log[OH⁻] = −log1.2 = 1.79
      pH= 14−pOH=14−1.79

           =12.21

(c) For 0.3 g of NaOH dissolved in water to give 200 mL of solution:

[OH⁻]= [NaOH] = 0.3×1000/200 ​= 1.5M
  pOH= −log[OH⁻] = −log1.5 = 1.43
     pH= 14 – pOH = 14 − 1.43

          = 12.57
(d) For 1mL of 13.6 M HCl diluted with water to give 1 L of solution:

The molarity of HCl solution after dilution is (13.6×1)/ 1000= 0.0136M.
It is equal to hydrogen ion concentration.
pH = −log[H⁺]= −log0.0136

      = 1.87

7.50. The degree of ionization of a 0.1 M bromoacetic acid solution is 0.132. Calculate the pH of the solution and the PK_a of bromoacetic acid.                            Answer: [H⁺] = cα = 0.1 × 0.132 = 0.0132M

  pH = −log[H⁺] = −log0.0132

        = 1.88

The acid dissociation constant is 

  K_a​ = cα²​ / (1−α) = 0.1 × (0.132)² / (1−0.132)

       ​= 2.01×10⁻³.

pK_a ​= −logK_a​ = −log(2.01×10⁻³) ≈ 2.7

7.51. The pH of 0.005 M codeine (C₁₈H₂₁N0₃) solution is 9.95. Calculate the ionization constant and PK_b.                                                                                         Answer:
      pH = 9.95, 

   pOH = 14 – pH = 14 − 9.95 = 4.05
[OH⁻] = 10^−pOH = 10^−4.05 = 8.913 × 10⁻⁵
                                    Codeine + H₂​O ⇌ Codeine^H+ + OH⁻

The ionization constant, K_b​= [CodeineH⁺][OH⁻] / [codeine]​

                                             = [(8.913×10⁻⁵)×(8.913×10⁻⁵)] / 5×10⁻³

                                             ​= 1.588×10⁻⁶.
                                      pK_b​ = −log(1.588×10⁻⁶)

                                             = 5.8

7.52. What is the pH of 0.001 M aniline solution? The ionization constant of aniline can be taken from Table 7.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.                          

Answer: Let c be the initial concentration of C₆H₅NH₃⁺ and x be the degree of ionisation.

                                                C₆H₅NH₂ + H₂O ​⇌  C₆H₅NH₃⁺ + OH^-

                                                     c(1-x)                      cx              cx

K_b = [C₆H₅NH₃⁺][ OH^-] / [C₆H₅NH₂]

     = [cx][cx] / [c(1 – x)]

Since x is very small and negligible 1 – x≈ 1

∴K_b= [cx][cx] / [c] = cx²

=> x =

         =  

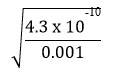
         = 6.56 x 10^-4

∴ [OH^-] = cx = 0.001 x 6.56 x 10^-4 = 6.56 x 10^-7 M

       [H⁺]= Kw / [OH^-] = 10^-14 / 6.56 x 10^-7 = 1.52 x 10^-8

         pH= –log[H⁺] = –log1.52 x 10^-8 = 7.818

∴ Ionization constant of the conjugate acid of aniline,

        K_a = K_w / K_b

            = 10^-14 / (4.3 x 10^-10)

            = 2.32 x 10^-5

7.53. Calculate the degree of ionization of 0.05M acetic acid if its pKa value is 4.74.

How is the degree of dissociation affected when its solution also contains

(a) 0.01M (b) 0.1M in HCl?                                                                                                

Answer: pKa​ = −logKa= 4.74
                  Ka​ = 10^−pKa =10^−4.74 = 1.8×10⁻⁵
Let x be the degree of dissociation. The concentration of acetic acid solution, C = 0.05 M
The degree of dissociation, 

                     x= (Ka / C)^1/2 ​​​= (1.8×10⁻⁵ / 0.05)^1/2 ​​= 0.019
(a) The solution is also 0.01 M in HCl.
Let x M be the hydrogen ion concentration from ionization of acetic acid. The hydrogen ion concentration from ionization of HCl is 0.01 M. The total hydrogen ion concentration
                [H⁺] = 0.01 + x
The acetate ion concentration is equal to the hydrogen ion concentration from ionization of acetic acid. This is also equal to the concentration of acetic acid that has dissociated.
[CH_3​COO⁻] = x
[CH_3​COOH] = 0.05 − x
         

          Ka ​= [H+][CH3​COO−]​ /[CH3​COOH]
1.8×10⁻⁵ = (0.01+x)x / (0.05−x) ​...(1)
As x is very small,  0.01 + x ≈ 0.01
0.05 – x ≈ 0.05
Hence, the equation (i) becomes
1.8×10⁻⁵ = 0.01x​ / 0.05
             x = 9.0×10⁻⁵M
The degree of ionization is  [CH₃​COO−]​ / [CH₃​COOH] = x / c ​

                                                                                          = (9.0×10⁻⁵) /0.05​

                                                                                         = 1.8×10⁻³= 0.0018.
(b) The solution is also 0.1 M in HCl.
Let x M be the hydrogen ion concentration from ionization of acetic acid. The hydrogen ion concentration from ionization of HCl is 0.01 M. The total hydrogen ion concentration
                        [H⁺] = 0.1 + x
The acetate ion concentration is equal to the hydrogen ion concentration from ionization of acetic acid. This is also equal to the concentration of acetic acid that has dissociated.
[CH_3​COO⁻] = x
[CH₃​COOH] = 0.05− x
          Ka​ = [H+][CH_3​COO⁻]​ / [CH₃​COOH]
1.8×10⁻⁵ = (0.1+x)x​ / (0.05−x) .....(1)
As x is very small,  0.1 + x ≈ 0.1
0.05 − x ≈ 0.05
Hence, the equation (i) becomes
1.8 × 10⁻⁵ = 0.1x/0.05​
               x = 9.0×10⁻⁶M
The degree of ionization is [CH3​COO⁻]​ / [CH3​COOH] = x/c ​= 9.0×10⁻⁶/ 0.05​

                                                                                           = 1.8 ×10⁻⁴ = 0.00018.

7.54. The ionization constant of dimethylamine is 5.4 × 10^–4. Calculate its degree of ionization in its 0.02M solution. What percentage of dimethylamine is ionized if the solution is also 0.1M in NaOH?                                                                                                                      

Answer: K_b= 5.4×10⁻⁴

   c= 0.02M

Then, α= (K_b /c)^1/2

       α= (5.4×10⁻⁴ / 2 x 10^-2)^1/2 =0.1643

(CH₃)₂NH+H₂O ↔ (CH₃)₂NH⁺₂+OH^-

   [(CH₃)₂NH] = 0.02 – x ≈ 0.02

[(CH₃)₂NH⁺₂] = x

             [OH^-] = 0.1 + x

                       ≈ 0.1

Now, K_b= [(CH3)2NH+2][OH−]/[(CH3)2NH] = (x × 0.1) / (0.025).

            x = 1.08 x 10^-4

% of dimethylamine ionised = (1.08 x 10^-4) x (100 / 0.02) = 0.54%

7.55. Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:

(a) Human muscle-fluid, 6.83                              (b) Human stomach fluid, 1.2

(c) Human blood, 7.38                                          (d) Human saliva, 6.4.                 

Ans: a. Human muscle fluid 6.83

pH=6.83

pH=−log[H⁺]

∴6.83=−log[H⁺]

[H⁺]= 1.48 x 10⁻⁷M

1. Human stomach fluid, 1.2:

pH=1.2

1.2=−log[H⁺]

∴[H⁺] = 0.063 M = 6.3 x 10^-2 M

7. Human blood, 7.38:

pH=7.38=−log[H⁺]

∴[H⁺]= 4.17 x 10⁻⁸M

6. Human saliva, 6.4:

pH=6.4

6.4=−log[H⁺]

[H⁺]= 3.98 x 10⁻⁷ M

7.56. The pH of milk, black coffee, tomato juice, lemon juice and egg white are 6.8, 5.0, 4.2, 2.2 and 7.8 respectively. Calculate corresponding hydrogen ion concentration in each.

 Answer: The hydrogen ion concentration in the given substances can be calculated by using the given relation: pH=−log[H⁺]

Hence, [H⁺] = 10^−pH
Milk: [H⁺] = 10^−6.8 = 1.58×10⁻⁷M
Black coffee: [H⁺] = 10^−5.0 =1×10⁻⁵M
Tomato juice: [H⁺] = 10^−4.2 =6.31×10⁻⁵M
Lemon juice: [H⁺]=10^−2.2 = 6.31×10⁻³M
Egg white: [H⁺]=10^−7.8=1.58×10⁻⁸M

7.57. If 0.561 g of KOH is dissolved in water to give 200 mL of solution at 298 K. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its pH?           

Ans: [KOH]=[K⁺]=[OH⁻]= (0.561×1000) / (56×200) ​=0.050M
[H+]=Kw / [OH⁻]​​=10⁻¹⁴ / 0.05 ​=2.0×10⁻¹³
pH=−log[H⁺]=−log(2.0×10⁻¹³)

     =12.7

7.58. The solubility of Sr(OH)₂ at 298 K is 19.23 g/L of solution. Calculate the concentrations of strontium and hydroxyl ions and the pH of the solution.              Answer: Solubility of Sr(OH)₂=19.23g/L

The molecular weight of Sr(OH)₂  is 87.6 + 2(17)=121.6

Then, concentration of Sr(OH)₂=19.23 /121.63M=0.1581M

Sr(OH)₂(aq)→Sr²⁺(aq)+2(OH⁻)(aq)

∴[Sr²⁺]=0.1581M

  [OH⁻]=2×0.1581M=0.3126M

Now,K_w=[OH⁻][H⁺]

=> [H+] = 10⁻¹⁴ / 0.3126

=>[H+]=3.2×10⁻¹⁴

      ∴pH= 13.495

7.59. The ionization constant of propanoic acid is 1.32 × 10^–5. Calculate the degree of ionization of the acid in its 0.05M solution and also its pH. What will be its degree of ionization if the solution is 0.01M in HCl also?                                                               

Answer: Let the degree of ionization of propanoic acid be α. Then, representing propionic acid as HA, we have:

                                                        HA         +        H₂O ⇔ H₃O⁺    +    A⁻

                                              (.05−0.0α)≈0.5                         0.05α      0.05α

K_a=[H₃O⁺][A⁻] / [HA]

    =(0.05α)(0.05α) / 0.05

    = 0.05α²

=> α = (K_a /0.05)^1/2

            =1.63×10⁻²

Then, [H₃O⁺]=.05α=.05×1.63×10⁻²= K_b.15×10⁻⁴M

∴pH=3.09

In the presence of 0.1M of HCl, let α' be the degree of ionization.

Then, [H₃O⁺]=0.01

[A⁻]= 005α′

[HA]=.05

K_a= (0.01×.05α′) /0.05

=>1.32×10⁻⁵=.01×α′

=>α′=1.32×10⁻³

 

7.60. The pHof 0.1M of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.                                 Answer: c=0.1M 

                 pH= −log[H⁺]

=>         2.34 = −log[H⁺]

So, −log[H⁺]= 2.34

=>          [H⁺]= 4.5×10⁻³

Also,

              [H⁺]= cα

=>  4.5×10⁻³= 0.1×α

=> α=4.5×10⁻²= 0.045

Then, 

Ka = α²/c = (45×10⁻³)²/ 0.1

      =202.5×10⁻⁶

      =2.02×10⁻⁴

7.61. The ionization constant of nitrous acid is 4.5×10⁻⁴. Calculate the pH of 0.04 M sodium nitrite solution and also its degree of hydrolysis.                                                                

Answer: Since NaNO₂ is the salt of a strong base (NaOH) and a weak acid (HNO₂);

                                                NO₂⁻ + H₂O ↔ HNO₂ + OH⁻

Then, K_b= [HNO₂][OH⁻] / [NO₂⁻]

⇒ Kw/ Ka = (10⁻¹⁴) / (4.5×10⁻⁴)

                  = 0.22×10⁻¹⁰

Now, if x moles of the salt undergo hydrolysis, and then the concentration of various species present in the solution will be:

 [NO₂⁻]= 0.04−x; 0.04

[HNO₂]= x

   [OH⁻]= x

         K_b= x² / 0.04

             = 0.22×10⁻¹⁰

          x²= 0.0088×10⁻¹⁰

           x= 0.093×10⁻⁵

∴ [OH⁻]= 0.093×10⁻⁵ M

[H₃O⁺]=10⁻¹⁴ / 0.093×10⁻⁵=10.75×10⁻⁹ M

⇒     pH= −log(10.75×10⁻⁹)=7.96

Now, degree of hydrolysis

            = x / 0.04= (0.093×10⁻⁵)/ 0.04

            = 2.325×10⁻⁵

7.62. A 0.02M solution of pyridinium hydrochloride has pH = 3.44. Calculate the ionization constant of pyridine.                                                                                         Answer: pH=3.44

We know that,

pH=−log[H⁺]

∴[H⁺]=3.63×10⁻⁴

Then, K_b=(3.63×10⁻⁴)² / 0.02(∵ concentration =0.02M)

⇒K_b=6.6×10⁻⁶

Now, K_b=K_w / K_a

⇒Ka=K_w / K_b=10⁻¹⁴ / 6.6×10⁻⁶=1.51×10⁻⁹

7.63. Predict if the solutions of the following salts are neutral, acidic or basic:

NaCl, KBr, NaCN, NH₄NO₃, NaNO₂ and KF                                                                  

Ans: (i) NaCl:

NaCl+H₂O↔NaOH+HCl

Strong base Strong acid

Therefore, it is a neutral solution.

(ii) KBr:

KBr+H₂O↔KOH+HBr

Strong base    Strong acid

Therefore, it is a neutral solution.

iii) NaCN:

NaCN+H₂O↔HCN+NaOH

Weak acid    Strong base

Therefore, it is a basic solution.

(iv) NH₄NO₃

NH₄NO₃+H₂O↔NH₄OH+HNO₃

Weak base    Strong acid

Therefore, it is an acidic solution.

(v) NaNO₂

NaNO₂+H₂O↔NaOH+HNO₂

Strong base    Weak acid

Therefore, it is a basic solution.

(vi) KF

KF+H₂O↔KOH+HF

Strong base   Weak acid

Therefore, it is a basic solution.

7.64. The ionization constant of chloroacetic acid is 1.35 × 10^–3. What will be the pH of 0.1M acid and its 0.1M sodium salt solution?                                                  Answer: Given K_a=1.35 x 10⁻³

For acid solution:

[H⁺] = (K_aC)^1/2 = (0.00135 x 0.1)^1/2 = 0.0116M

   pH = – log[H⁺] = –log0.0116 = 1.936

For 0.1M sodium salt solution

ClCH₂COONa is the salt of a weak acid i.e., ClCH₂COOH and a strong base i.e., NaOH.

pK_a = -logK_a = log(0.00135) = 2.8697

pK_w = 14

logc = log0.1 = −1

pH = 0.5[pK_w + pK_a + logc] = 0.5[14 + 2.8697 -1]

      = 7.935

7.65. Ionic product of water at 310 K is 2.7 × 10^–14. What is the pH of neutral water at this temperature?                                                                                               Answer: Ionic product,

K_w=[H⁺][OH⁻]

Let [H⁺]= x

Since [H⁺]= [OH⁻], Kw=x². 

⇒K_w at 310K is 2.7×10⁻¹⁴

∴2.7×10⁻¹⁴=x²

⇒x=1.64×10⁻⁷

⇒ [H⁺]=1.64×10⁻⁷

⇒ pH= −log[H⁺]=−log[1.64×10⁻⁷]=6.78

Hence, the pH of neutral water is 6.78.

7.66. Calculate the pH of the resultant mixtures:

1. a) 10 mL of 0.2M Ca(OH)₂ + 25 mL of 0.1M HCl
2. b) 10 mL of 0.01M H₂SO₄ + 10 mL of 0.01M Ca(OH)₂
3. c) 10 mL of 0.1M H₂SO₄ + 10 mL of 0.1M KOH

Answer: (a) Total number of moles present in 10 mL of 0.2 M calcium hydroxide are (10×0.2) / 1000​ = 0.002 moles.
Total number of moles present in 25 mL of 0.1 M HCl are (25×2) / 1000 ​= 0.0025 moles.
                                    Ca(OH)_2​ + 2HCl → CaCl₂​ + 2H₂​O
1 mole of calcium hydroxide reacts with 2 moles of HCl.
0.0025 moles of HCl will react with 0.00125 moles of calcium hydroxide.
Total number of moles of calcium hydroxide unreacted are 0.002−0.00125 = 0.00075 moles.
Total volume of the solution is 10 + 25 = 35 mL.
The molarity of the solution is (0.00075×1000) / 35 ​= 0.0214M
[OH⁻] = 2 × 0.0214 = 0.0428M
pOH = −log0.0428 = 1.368
pH = 14 − pOH

      = 14 − 1.368 = 12.635

(b) Total number of moles present in 10 mL of 0.01 M H₂​SO₄​ is (10×0.01) / 1000 ​= 0.0001 mol.
Total number of moles present in 10 mL of 0.01 M Ca(OH)₂ ​= (10×0.01) / 1000 ​= 0.0001 mole.
Ca(OH)₂ ​+ H₂​SO₄​ → CaSO₄ ​+ 2H_2​O
0.0001 mole of Ca(OH)₂​ will react completely with 0.0001 mole of H₂​SO₄ ​.
Hence, the resulting solution is neutral with pH 7.0.

(c) Total number of moles in 10 mL of 0.1 M H₂​SO₄ ​= (10×0.1) / 1000 ​= 0.001 mole.
Total number of moles present in 10 mL of 0.1 M KOH =(10×0.1​) / 1000 = 0.001 mole.
2KOH + H₂​SO₄ ​→ K₂​SO₄​ + 2H₂​O
2 moles of KOH reacts with 1 mole of H₂​SO₄.
0.001 mole of KOH will react with 0.0005 mole of H₂​SO₄ ​.
Number of moles of H₂​SO₄ left = 0.001−0.0005 = 0.005M
Volume of solution is 10+10 = 20mL
Molarity of the solution is (0.0005×1000​) / 20 = 0.025M.
[H⁺] = 2 × 2.5 × 10⁻² = 0.05M
pH = −log [H⁺] = −log0.05 = 1.3.

7.67. Determine the solubility of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298K from their solubility product constants given in Table 7.9 (page 221). Determine also the molarities of individual ions.                            

Answer:

1. Silver chromate:

Ag₂CrO₄→2Ag⁺+CrO₄²⁻

Then, [Ag⁺] = (2s), [CrO₄²⁻] = s

K_sp=[Ag⁺]²[CrO₄²⁻]

s = 0.65×10⁻⁴M

So, [Ag⁺] = 2s = 1.30 x 10⁻⁴M, [CrO₄²⁻] = 6.5 x 10^-5M

2. Barium Chromate:

BaCrO₄→Ba²⁺+CrO₄²⁻

[Ba²⁺] = [CrO₄²⁻] = s

Then, K_sp=[Ba²⁺][CrO₄²⁻] = s x s

= > 1.2 x 10^-10M = s²

= > s = 1.09 x 10^-5M

3. Ferric Hydroxide:

Fe(OH)₃→Fe³⁺ + 3OH⁻

Then [Fe³⁺] = s, [OH⁻] = 3s

K_sp=[Fe³⁺][OH⁻]³

Let s be the solubility of Fe(OH)₃

[Fe³⁺] = s = 1.38 x 10^-10M

[OH⁻] = 3s = 4.14 x 10^-10M

4. Lead Chloride:

PbCl₂→Pb²⁺+2Cl⁻

Then, [Pb²⁺] = s, [Cl⁻] = 2s

K_sp=[Pb²⁺][Cl⁻]²

= >Ksp=s x (2s)² =4s³ 

⇒1.6×10⁻⁵=4s³

⇒0.4×10⁻⁵=s³ 

=>4×10⁻⁶=s³

[Pb²⁺] = s=1.58×10⁻²M

[Cl⁻] = 2s=3.16×10⁻²M

5. Mercurous Iodide:

Hg₂I₂→ 2Hg⁺+2I⁻

[Hg²⁺] = [I⁻] = 2s

K_sp=[Hg²⁺]²[I⁻]²

=>4.5 x 10^-29 = (2s)²(2s)² = 16s⁴

=> s = 4.09 x 10^-8 M

 Therefore, [Hg²⁺] = [I⁻] = 2s = 8.18 x 10^-8 M

7.68. The solubility product constant of Ag₂CrO₄ and AgBr are 1.1×10⁻¹²and 5.0×10^-13 respectively. Calculate the ratio of the molarities of their saturated solutions.

Answer: Silver chromate: Ag₂CrO₄​ ⇌ 2Ag⁺ + CrO₄^2−​
[Ag⁺] = 2s₁​, CrO₄²⁻ ​= s₁​
K_sp ​= (2s₁​)²(s₁​) = 4s³ = 1.1×10⁻¹²
s_1​ = 6.5 × 10−5 .....(1)
Silver bromide: AgBr⇌ Ag⁺ + Br⁻
[Ag⁺] = [Br⁻] = s₂​
   Ksp​ = (s₂​) × (s₂​) = (s₂)² ​= 5.0 × 10⁻¹³
s_2​=7.07×10⁻⁷......(2)
Divide equation (1) by equation (2) to obtain the ratio of the molarities of saturated solutions:
​s₁/s₂​​= (6.50×10⁻⁵)/ (7.07×10⁻⁷) ​= 91.9 

7.69. Equal volumes of 0.002 M solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate? (For cupric iodate, Ksp = 7.4 × 10^–8).  

 Answer: After mixing, the concentration of NaIO₃​ is 0.002 / 2 ​=0.001M.
After mixing, the concentration of Cu(ClO_3​)_2​ is 0.002​/ 2 =0.001M.
NaIO₃​⇌Na⁺+IO₃⁻​
[IO₃⁻​]=0.001M
Cu(ClO₃​)₂​⇌Cu²⁺+2ClO₃⁻​
[Cu²⁺]=0.001M
The ionic product of Cu(IO₃​)₂​ is
[Cu²⁺][I⁻]²=0.001×0.001²=1×10⁻⁹
As the ionic product is less than the solubility product, no precipitation will occur.

 7.70. The ionization constant of benzoic acid is 6.46×10⁻⁵ and Ksp for silver benzoate is 2.5×10⁻¹³. How many times is silver benzoate more soluble in a buffer of pH= 3.19 compared to its solubility in pure water?                                                                                   

Ans:  Since pH=3.19, 

[H3O⁺]=6.46×10⁻⁴M

C₆H₅COOH+H₂O↔C₆H₅COO⁻+H₃O 

K_a=[C₆H₅COO⁻][H₃O⁺] / [C₆H₅COOH] 

[C₆H₅COOH] / [C₆H₅COO⁻]= [H₃O⁺] / Ka=6.46×10⁻⁴ / 6.46×10⁻⁵=10

Let the solubility of C₆H₅COOAg be xmol/L.

Then,

[Ag⁺]=x

[C₆H₅COOH]+[C₆H₅COO⁻]=x 

10[C₆H₅COO⁻]+[C₆H₅COO⁻]=x 

[C₆H₅COO⁻]=x / 11 

K_sp = [Ag⁺][C₆H₅COO⁻] 

= >2.5×10⁻¹3=x(x / 11)

= >x=1.66×10⁻⁶mol/L

Thus, the solubility of silver benzoate in a pH3.19 solution is 1.66×10⁻⁶mol/L.

Now, let the solubility of C₆H₅COOAg be x′mol/L.

Then, [Ag⁺]=x′Mand [C6H5COO⁻]=x′M

K_sp=[Ag⁺][C6H5COO⁻] 

Ksp=(x′)²

x′= (Ksp)^1/2= (2.5×10⁻¹³)^1/2 = 5×10⁻⁷mol/L

∴x / x′= (1.66×10⁻⁶) / (5×10⁻⁷) =3.32

Hence, C₆H₅COOAg is approximately 3.317 times more soluble in a low pH solution.

7.71. What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, there is no precipitation of iron sulphide?

(For iron sulphide, K_sp=6.3 x 10⁻¹⁸)                                                                               

Ans:  Let the maximum concentration of each solution be x mol/L. After mixing, the volume of the concentrations of each solution will be reduced to half i.e., x/2.

∴[FeSO₄]=[Na₂S]=x / 2

Then, [Fe2⁺]=[FeSO₄]=x/ 2

Also, [S²⁻]=[Na₂S]=x/2

FeS(x)↔Fe²⁺(aq)+S²⁻(aq)

K_sp=[Fe²⁺][S²⁻]

= >6.3×10⁻¹⁸=(x/2)(x/2)

x²/4=6.3×10⁻¹⁸

⇒x= 5.02×10⁻⁹

If the concentrations of both solutions are equal to or less than 5.02×10⁻⁹M, then there will be no precipitation of iron sulphide.

7.72 What is the minimum volume of water required to dissolve 1g of calcium sulphate at 298 K? (For calcium sulphate, K_sp is 9.1 x 10⁻⁶).

Ans:  CaSO₄(s)↔Ca²⁺(aq)+SO²⁻₄(aq)

Ksp=[Ca²⁺][ SO²⁻₄]

Let the solubility of CaSO4 be s.

[Ca²⁺] = [ SO²⁻₄] = s

Then, Ksp=s²

9.1×10−6=s²

s =3.02×10⁻³mol/L

Molecular mass of CaSO₄=136g/mol

Solubility of CaSO₄ in gram/L= 3.02×10⁻³×136=0.41g/L

This means that we need 1L of water to dissolve 0.41g of CaSO₄.

Therefore, to dissolve 1g of CaSO₄ we require = 10.41L= 2.44Lof water.

7.73 The concentration of sulphide ion in 0.1M HCl solution saturated with hydrogen sulphide is 1.0 × 10^–19 M. If 10 mL of this is added to 5 mL of 0.04 M solution of the following: FeSO₄, MnCl₂, ZnCl₂ and CdCl₂. in which of these solutions precipitation will take place?

Answer: For precipitation to take place, it is required that the calculated ionic product exceeds the K_sp value. So, following data on K_sp values should have been provided to answer the question.

KspforFeS=6.3×10⁻¹⁸,

MnS=2.5×10⁻¹³,

ZnS=1.6×10⁻²⁴

CdS=8.0×10⁻²⁷

Before mixing:

[S²⁻]=1.0×10⁻¹⁹M and [M²⁺]=0.04M 

volume =10mL volume =5mL 

After mixing:

[S²⁻]=?[M²⁺]=? 

volume =(10+5)=15mL volume =15mL 

[S²⁻]= (1.0×10⁻¹⁹×10)/ 15=6.67×10⁻²⁰M

[M²⁺]= (0.04×5) / 15=1.33×10⁻²M

Ionic product =[M²⁺][S²⁻] 

           =(1.33×10⁻²)(6.67×10⁻²⁰)

           =8.87×10⁻²²

This ionic product exceeds the Ksp of ZnS and CdS. Therefore, precipitation will occur in CdCl₂ and ZnCl₂ solutions.