We have compiled a comprehensive collection of previous JEE Advanced Maths questions, organised by year, along with a separate list of the 11 most difficult JEE Advanced maths questions from the past decade. Continue reading for all the details.
JEE Advanced Maths Questions: The Maths part of the JEE Advanced exam has always been a concern for the aspirants. And this is so because JEE Advanced maths questions has the lengthiest calculations.
Explore colleges based on JEE Advanced
The Maths part of the JEE Advanced exam has 17 questions and carries 60 marks. On the JEE Advanced exam day, candidates get instructions and details about the JEE Advanced exam pattern, along with the JEE Advanced question paper itself.
Most of the questions in the JEE Advanced maths section usually come from functions, limits, and how to apply concepts related to derivatives. Candidates will also encounter questions about definite integrals, calculating areas under curves, and working with inverse trigonometric functions, three dimensions, as well as shapes like circles, parabolas, and probability.
JEE Advanced Maths questions from previous year are made available on this page. Also, we have curated the most difficult JEE Advanced Maths questions asked over the past few years.
- 11 Most Difficult JEE Advanced Maths Questions Over the Past Years
- All JEE Advanced Maths Questions From Previous Years
- JEE Advanced Maths Section Overview
11 Most Difficult JEE Advanced Maths Questions Over the Past Years
As per the experts’ analysis, here are the top 11 toughest maths questions that have been asked in the JEE Advanced exam over the past few years:
Q1: Let [M] denote the determinant of a square
Let g: [0,π/2] → R be the function defined by
Where,
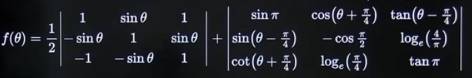
Let p(x) be a quadratic polynomial whose roots are the maximum and minimum values of the function g(θ) and P(2) = 2 -√2, then, (JEE Advanced 2022, Paper 1)
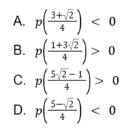
Ans: A and C
Q2: Let

- a = 0, k = 8
- 4a-k+8=0
- det(Padj(Q)) = 29
- det(Qadj(P)) = 213
Ans: B and C
Q3: Let a and ẞ be the roots of x2 - x - 1 = 0 a > β. For all positive integers n, define an = (αn- βn)/a- β >= 1, b1 = 1 and bn = an-1+an+1, n >= 2. Then which of the following options is/are correct? (JEE Advanced 2019, Paper 1)
- ∞∑n=1 bn/10n = 8/89
- bn = αn + βn for all n>=1
- a1+a2+a3+....+an = an+2 - 1
- ∞∑n=1 an/10n = 10/89
Ans: B, C and D
Q4: Let Sn = 4n∑k=1(-1)k(k+1)/2K2. Then Sn can take value(s). (JEE Advanced 2013, Paper 1)
- 1056
- 1088
- 1120
- 1332
Ans: A and D
Q5:
- g (m, n) = g (n, m) for all positive integers m, n
- g (m, n+1) = g (m+1, n) for all positive integers m, n
- g (2m, 2n) = 2g (m, n) for all positive integers m, n
- g (m,n) = (g (n,m))2 for all positive integers m, n
Ans: A, B and D
Q6: Let |X| denote the number of elements in a set X. Let S = {1, 2, 3, 4, 5, 6} be a sample space, where each element is equally likely to occur. If A and B are independent events associated with S, then the number of ordered pairs (A, B) such that 1≤ |B|<|A|, equals (JEE Advanced 2019, Paper 2)
Ans: 422
Q7: Considering only the principal values of the inverse trigonometric functions, the value of is___________ (JEE Advanced 2022, Paper 1)
Ans: 3π/4
Q8: 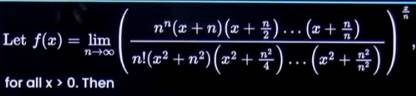
- f(1/2) >= f(1)
- f(1/3) <= f(2/3)
- f'(2) <= 0
- f'(3)/f(3) >= f'(2)/f(2)
Ans: B
Q9: Let ABC be the triangle with AB = 1, AC = 3 and ∠BAC = π/2. If a circle of radius r > 0 touches the sides AB, AC and also touches internally the circumcircle of the triangle ABC, then the value of r is (JEE Advanced 2022, Paper 1)
Ans: 0.83 or 0.84
Q10: Consider the hyperbola x2/100 - y2/64 = 1 with foci at S and S1, where S lies on the positive x-axis. Let P be a point on the hyperbola, in the first quadrant. Let ∠SPS = α, with a < π/2. The straight line passing through the point s and having the same slope as that of the tangent at P to the hyperbola, intersects the straight line S1P at P1. Let δ be the distance of P from the straight line SP1 and β = S1P. Then the greatest integer less than or equal to βδ/9.sinα/2 is ____________ (JEE Advanced 2022, Paper 2)
Ans: 7.11
Q11: Let R³ denote the 3-D space. Take two points P(1, 2, 3) and Q(4, 2, 7). Let dist(X, Y) denote the distance between two points X and Y in R³.
Let S = {X ∈ R³ : (dist(X, P))2 - (dist(X, Q))² = 50} and
T = {Y ∈ R³: (dist(Y, Q))2 - (dist(Y, P))² = 50}
Then which of the following statements is (are) TRUE? (JEE Advanced 2024, Paper 1)
- There is a triangle whose area is 1 and all of whose vertices are from S.
- There are two distinct points Land M in T such that each point on the line segment LM is also in T.
- There are infinitely many rectangles of perimeter 48, two of whose vertices are from S and the other two vertices are from T.
- There is a square of perimeter 48, two of whose vertices are from S and the other two vertices are from T.
Ans: All four options are correct
Also Read:
- JEE Advanced Syllabus for Chemistry
- JEE Advanced Syllabus for Physics
- JEE Advanced Syllabus for Mathematics
All JEE Advanced Maths Questions From Previous Years
Above we curated and provided you the most difficult questions in JEE Advanced Maths over the past 10 years. However, candidates who wish to have all the previous year JEE Advanced maths questions for practice, can download the PDF files below:
JEE Advanced Maths Questions with Solutions 2024 to 2019:
Check below the JEE Advanced Maths questions with solutions PDF:
| Year |
JEE Advanced Maths questions with solutions |
|---|---|
| 2024 |
Paper 1 - Download here Paper 2 - Download here |
| 2023 |
Paper 1 - Download PDF Paper 2 - Download PDF |
| 2022 |
Paper 1 - Download PDF Paper 2 - Download PDF |
| 2021 |
Paper 1 - Download PDF Paper 2 - Download PDF |
| 2020 |
Paper 1 - Download PDF Paper 2 - Download PDF |
| 2019 |
Paper 1 - Download PDF Paper 2 - Download PDF |
Also Check:
| JEE Advanced Physics Questions | JEE Advanced Chemistry Questions |
JEE Advanced Maths Section Overview
Check below the details regarding the JEE Advanced maths section in JEE Advanced question paper followed in the past 2 years:
Total Marks in JEE Advanced Maths section: 120
- 60 marks in JEE Advanced paper 1
- 60 marks in JEE Advanced paper 2
In each paper of JEE Advanced, the Maths section has the following sections:
- Sec-I (Max. marks-12)
- Sec-II (Max. Marks-12)
- Sec-III (Max. marks-24)
- Sec-IV (Max. marks-12)
Number of questions and marks distribution in each of the sections is as follows:
| Section |
Number of questions and total marks |
Marking Scheme |
|---|---|---|
| 1 |
4 questions of 12 marks |
|
| 2 |
3 questions of 12 marks |
|
| 3 |
6 questions of 24 marks |
|
| 4 |
4 questions of 12 marks |
|
Read More:
You can prepare for all entrance tests at same time. It is a tough task but not impossible. For this a proper strategy is required. Here are some important tips.
- Compare the syllabus: All engineering entrance exams have almost the same syllabus. There might be some additional topics in some exams. The aspirant must study the syllabus for all exams and find out the topics that are extra, and prepare those separately. Almost 90% of the topics will be common for all entrance exams, and hence, syllabus completion for one exam will lead to completion of the syllabus for all the exams.
- Prepare for JEE Mains and incorporate the preparation for all other exams: Apart from JEE Advanced, all the exams are pretty straightforward for a well-prepared candidate. JEE Advanced require a higher level of preparation as the questions are multi-conceptual. However, the state-level entrance exams, and exams like BITSAT, VITEEE, etc., have direct questions. Most of the questions in JEE Mains are also direct and require the application of basic concepts. Hence, the candidates must prepare for one exam, like JEE Mains, that will cover their preparation for all other exams.
- JEE Advanced needs extra effort: For JEE Advanced candidates must focus on time management and building exam day temperament. Learn how to apply multiple concepts to a question.
The bottom line is to prepare for JEE Mains to cover the preparation for all other CETs and exams like BITSAT and VITEEE. For JEE Advanced, work on sharpening your skills of time management, stress handling, multiple concept application, speed and accuracy.
So far no student has ever scored full marks in JEE Advanced signifies exam's difficulty level. Highest marks one has achieved to date in JEE Advanced are 355 marks out of 360. Ved Lahoti scored these marks in 2024.
There is no seperate rank list released for JEE Advanced. The rank of the candidates in All India category and in the respective category of the candidate is meantioned on the result itslef.
As per the analysis of the previous year data, the candidates belonging to general category must aim to score around 180 marks out of 360 to qualify the exam. However, note that this marks will not get you a good rank and hence tier 1 IITs (IIT B, IIT M, IIT D) and courses will be out of reach.
| Name of Institute | NIRF Ranking 2025 |
|---|---|
| IIT Madras | 1 |
| IIT Delhi | 2 |
| IIT Bombay | 3 |
| IIT Kanpur | 4 |
| IIT Kharagpur | 5 |
| IIT Roorkee | 6 |
| IIT Hyderabad | 7 |
| IIT Guwahati | 8 |
| IIT BHU | 10 |

Currently - Assistant Manager, Content
Role - News and Feature Writer, Content Editor
Expertise - Engineering Education and Counselling
Mamona Majumder specialises in news and feature writing, and content editing. W
Read Full BioNews & Updates
Explore Other Exams
Jan '26 | JEE Main 2026 City Intimation ... |
Jan '26 | JEE Main Admit Card 2026 Sessi... |
3 Nov '25 - 16 Apr '26 | SRMJEEE 2026 Registration (Pha... |
3 Nov '25 - 4 Jun '26 | SRMJEEE 2026 Registration (Pha... |
Feb '26 | COMEDK application form 2026 |
May '26 | COMEDK exam date 2026 |
1 Oct '25 - 15 Mar '26 | MET 2026 application form - Ph... |
Mar '26 | MET 2026 application form - Ph... |
15 Dec '25 - 16 Mar '26 | BITSAT 2026 application form -... |
Mar '26 | BITSAT 2026 Form Correction - ... |
Feb '26 | TS EAMCET 2026 notification |
Mar '26 | TS EAMCET 2026 application for... |
Student Forum
Answered Yesterday
Overall, 50-55% seats are reserved in IITs. The break-up of reservation is - 27% for OBC-NCL, 15% for SC, 7.5% for ST, 10% for Gen-EWS and 5% horizontal reservation for PwD candidates.
S
Contributor-Level 10
Answered Yesterday
Physics is the most difficult of all three subjects asked in the JEE Advanced exam. Many students also finds Maths as the toughest. It largely depends upon the understanding of candidates and how well the students are equipped with basic knowledge of any subject.
S
Contributor-Level 10
Answered Yesterday
It is mandatory to appear in both papers of JEE Advanced exam. The total marks are calculated by adding the sum of scores in both papers.
S
Contributor-Level 10
Answered a week ago
JEE Advanced question paper will be available online on the website jeeadv.ac.in. IIT Roorkee will release both paper 1 and 2 on the same day or the next day of exam.
S
Contributor-Level 10
Answered a week ago
JEE Advanced question paper 2026 will be released by IIT Roorke after the exam. The question paper is usually released on the same day or the next day of the exam. Candidates will be provided the download link ofthe paper on this page once released.
S
Contributor-Level 10
Answered a month ago
Candidates should ideally try to solve at least 3 previous year JEE question papers per week. However, candidates can also increase the frequency of this to 5 to 6 papers per week, one month before the exam.
M
Contributor-Level 6
Answered 2 months ago
Well, becoming a rocket scientist is a long-term commitment, and it depends on your education path and goals It takes almost 5 to 6 years with a bachelor's and 8 to 12 years if you want to study higher. Here below is how long it usually takes:
- Bachelor's degree: You have to study aeronautical enginee
Answered 2 months ago
Who work on the rocket-propelled vehicles, they apply the principles of Mathematics, Physics, and Material Science to solve challenges related to these vehicles. Rocket Scientists are involved in the process of design and development of the vehicles such as small drones, satellites, and commercial a
L
Beginner-Level 2
Answered 2 months ago
Yes, this field is considered hard. It is complex and demands high precision. There can be extreme consequences for minor errors. The overall field is extremely challenging as it requires to apply the basic scientific principles to design and develop rockets. It requires sophisticated engineering wi
P
Beginner-Level 2
Answered 2 months ago
The following are the qualification which can help you to become a rocket scientist:
· Bachelor's Degree such as B.Tech/B.E can take up to four years to complete.
· You can do a two years Master's Degree M.Tech/M.E./M.S. after graduation.
· For advanced level study in this field, you
C
Beginner-Level 2
 Exam On - 17 May '26
Exam On - 17 May '26





Preparation for JEE Advanced begins by knowing exam syllabus. Every student must follow syllabus. Once preparation is done then start solving previous year questions for self-assessment. This will give an overview of your preparation.