CUET Mathematics 2026 will be conducted in May in CBT Mode. Candidates preparing for the Mathematics/ Applied Mathematics exam must check this article to learn about the CUET 2026 Mathematics Syllabus, exam pattern, important chapters, previous years' papers, and preparation books.
NTA has released the CUET Mathematics Syllabus on its official website. Candidates preparing for the CUET for UG admissions for the academic cycle 2026-2027 must thoroughly familiarize themselves with the CUET syllabus. Mathematics/Applied Mathematics is one top three CUET domain subjects, and according to the National Testing Agency, the CUET Mathematics question paper includes 50 questions. The candidates appearing for CUET are required to attempt all questions within 60 minutes. Read this article to get the direct link to download the CUET Mathematics Syllabus PDF. NTA has made a few changes in syllabus.
National Testing Agency will administer mathematics exam between May 11 and May 31, 2026, in Computer Based Test mode. Candidates who will fill CUET application form 2026 on or before January 30, 2026, will be eligible to appear for the exam. The registration forms were released on January 03, 2026 at cuet.nta.nic.in. Check out the article for detailed information on the CUET mathematics exam.
Latest Update:
CUET UG general test will cover the topics from the following:
- General Knowledge, Current Affairs
- General mental ability, Numerical ability
- Reasoning (Simple application of basic Mathematical concepts, quantitative arithmetic, algebra geometry, mensuration and statistics)
- Logical and analytical reasoning
Candidates preparing for the general test of CUET UG are advised to stay updated with the current affairs by reading the newspapers and magazines. Candidates must gather study materials to prepare for the syllabus of General test and practice ample questions to become familiar with the type of questions asked in this section. Download the CUET UG question paper now.
No, class 11th subject syllabus is not included in CUET UG exam. Students who are preparing for CUET 2026 exam must focus on class 12th NCERT curriculum. NTA prescribes the CUET UG syllabus on its official website. Candidates must be familar the detailed syllabus mentioned on the NTA CUET official website- cuet.nta.nic.in. However, for better concepts clarity, candidates may refer to the class 11th resources.
NTA CUET 2026 exam will be scheduled in May/June 2026 tentatively. Candidates preparing for board examinations must prepare well for the CUET exam along.
CUET 2026 Registration Begins; Common Mistakes to Avoid for Undergraduate Admissions
CUET Registration 2026 Underway; Why Subject Combination is Important for UG Admissions?
- CUET 2026 Mathematics Syllabus: Highlights
- CUET UG Mathematics/ Applied Mathematics Syllabus 2026
- CUET Maths Syllabus 2026: Section A1
- CUET Maths Syllabus 2026: Section B1 (Mathematics)
- CUET Maths Syllabus 2026: Section B2 (Applied Mathematics)
- CUET Mathematics Syllabus PDF Download
- CUET UG Subjects: Question Paper & Syllabus PDFs
- Best Books for CUET Mathematics Preparation
CUET 2026 Mathematics Syllabus: Highlights
Refer to the table below to know the key details related to CUET Mathematics Syllabus:
Explore colleges based on CUET
| Particulars |
Details |
|---|---|
| CUET Exam Conducting Body |
National Testing Agency |
| Mode of the examination |
Computer-Based Test Mode |
| Language of exam |
13 languages - English, Hindi, Assamese, Bengali, Gujarati, Kannada, Malayalam, Marathi, Odia, Punjabi, Tamil, Telugu, and Urdu |
| Type of questions |
Multiple Choice Questions (MCQs) |
| Total number of Questions |
50 questions (all compulsory) |
| Duration of Exam |
60 minutes |
| Maximum Marks |
250 per subject |
| Negative marking |
Yes |
| Marking Scheme |
+5 for each correct answer -1 for each incorrect answer |
| CUET Mathematics Mapping for Courses |
B.Sc. Mathematics |
Also Read: CUET Mathematics Exam Pattern
CUET UG Mathematics/ Applied Mathematics Syllabus 2026
Candidates can check the CUET syllabus 2026 for Mathematics/ Applied Mathematics from the table given below.
| CUET Mathematics Syllabus: Unit-Wise | |
|---|---|
| Section A1 | |
| Unit I: Algebra | Unit IV: Differential Equations |
| Unit II: Calculus | Unit V: Probability Distributions |
| Unit III: Integration and its Applications | Unit VI: Linear Programming |
| Section B1 | |
| Unit I: Relations And Functions | Unit IV: Vectors And Three Dimensional Geometry |
| Unit II: Algebra | Unit V: Linear Programming |
| Unit III: Calculus | Unit VI: Probability |
| Section B2: Applied Mathematics | |
| Unit I: Numbers, Quantification and Numerical Applications | UNIT V: Index Numbers and Time Based Data |
| UNIT II: Algebra | UNIT VI: Infrential Statistics |
| UNIT III: Calculus | UNIT VII: Financial Mathematics |
| UNIT IV: Probability Distributions | UNIT VIII: Linear Programming |
CUET Maths Syllabus 2026: Section A1
Refer to this table for CUET 2026 maths syllabus for Section A1.
| Units | |
|---|---|
| Unit I: Algebra
|
Unit IV: Differential Equations
|
| Unit II: Calculus
|
Unit V: Probability Distributions
|
| Unit III: Integration and its Applications
|
Unit VI: Linear Programming
|
CUET Maths Syllabus 2026: Section B1 (Mathematics)
Check detailed syllabus for Section B1 of CUET Mathematics 2026 here.
Unit I: Relations And Functions
- Relations and Functions: Types of relations: Reflexive, symmetric, transitive and equivalence relations. One to one and onto functions.
- Inverse Trigonometric Functions: Definition, range, domain, principal value branches. Graphs of inverse trigonometric functions.
Unit II: Algebra
Matrices:
- Concept, notation, order, equality, types of matrices, zero matrix, transpose of a matrix, symmetric and skew symmetric matrices.
- Operations on matrices: Addition, multiplication and multiplication with a scalar. Simple properties of addition, multiplication and scalar multiplication.
- Non-commutativity of multiplication of matrices and existence of non-zero matrices whose product isthe zero matrix (restrict to square matrices of order 2).
- Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).
Determinants:
- Determinant of a square matrix (upto 3×3 matrices), minors, co-factors and applications of determinants in finding the area of a triangle.
- Adjoint and inverse of a square matrix.
- Consistency, inconsistency and number of solutions of system of linear equations by examples
- Solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
Unit III: Calculus
Continuity and Differentiability:
- Continuity and differentiability, chain rule, derivatives of inverse trigonometric functions, like sin-1x, cos-1x, and tan-1x, derivative of implicit functions.
- Concepts of exponential, logarithmic functions.
- Derivatives of logarithmic and exponential functions.
- Logarithmic differentiation, derivative of functions expressed in parametric forms.
- Second-order derivatives.
Applications of Derivatives:
- Rate of change of quantities, increasing/decreasing functions, maxima and minima (first derivative test motivated geometrically and second derivative test given as provable tool).
- Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).
Integrals:
- Integration as inverse process of differentiation.
- Integration of a variety of functions by substitution, by partial fractions and by parts,
- Evaluation of simple integrals of the following types and problems based on them:
- Fundamental Theorem of Calculus(without proof).
- Basic properties of definite integrals and evaluation of definite integrals.
Applications of the Integrals:
- Applications in finding the area under simple curves, especially lines, circles/parabolas/ellipses(in standard form only).
Differential Equations:
- Definition, order and degree, general and particular solutions of a differential equation.
- Solution of differential equations by method of separation of variables, solutions of homogeneous differential equations of first order and first degree.
- Solutions of linear differential equation of the type:
Check Out: CUET UG Login
Unit IV: Vectors And Three Dimensional Geometry
Vectors:
- Vectors and scalars, magnitude and direction of a vector.
- Direction cosines and direction ratios of a vector.
- Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio.
- Definition, Geometrical interpretation, properties and application of scalar (dot) product of vectors, vector(cross) product ofvectors
Three-dimensional Geometry:
- Direction cosines and direction ratios of a line joining two points.
- Cartesian equation and vector equation of a line, skew lines, shortest distance between two lines.
- Angle between two lines.
Unit V: Linear Programming
Introduction, related terminology such as constraints, objective function, optimization, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).
Unit VI: Probability
- Conditional probability, Multiplications theorem on probability, independent events, total probability, Baye’s theorem.
- Random variable
Also Read: CUET Maths Important Topics & Chapter Wise Weightage
CUET Maths Syllabus 2026: Section B2 (Applied Mathematics)
Get detailed topic-wise syllabus for Section B2 of CUET Mathematics. The section B2 includes topics related to applied mathematics.
Unit I: Numbers, Quantification and Numerical Applications
Modulo Arithmetic
- Define Modulus of an Integer
- Apply Arithmetic Operations using Modular Arithmetic Rules
Congruence Modulo
- Define Congruence Modulo
- Apply the definition in various problems
Allegation and Mixture
- Understand the rule of allegation to produce a mixture at a given price
- Determine the mean price of a mixture
- Apply rule of allegation
Numerical Problems
- Solve real life problems mathematically
Boats and Streams
- Distinguish between upstream and downstream
- Express the problem in the form of an equation
Pipes and Cisterns
- Determine the time taken by two or more pipes to fill or empty the tank
Races and Games
- Compare the performance of two players w.r.t. time, distance
Numerical Inequalities
- Describe the basic concepts of numerical inequalities
- Understand and write numerical inequalities
UNIT II: Algebra
Matrices and types of matrices
- Define matrix
- Identify different kinds of matrices
Equality of matrices, Transpose of a matrix, Symmetric and Skew symmetric matrix
- Determine equality of two matrices
- Write transpose of given matrix
- Define symmetric and skew symmetric matrix
Algebra of Matrices
- Perform operations like addition & subtraction on matrices of same order
- Perform multiplication of two matrices of appropriate order
- Perform multiplication of a scalar with matrix
Determinant of Matrices
- Determinant of a square matrix
- Use elementary properties of determinants
- Singular matrix, Non-singular matrix
- |AB|=|A||B|
- Simple problems to find determinant value
Inverse of a Matrix
- Define the inverse of a square matrix
- Apply properties of inverse of matrices
- Inverse of a matrix using: a) cofactors
If A and B are invertible square matrices of same size- (AB)-1 = B-1A-1
- (A-1)-1 = A
- (AT)-1 = (A-1)T
Solving system of simultaneous equations (upto three variables only (non-homogeneous equations))
UNIT III: Calculus
Higher Order Derivatives
- Determine second and higher-order derivatives upto second order derivatives
- Understand the differentiation of parametric functions and implicit functions
Application of Derivatives
- Determine the rate of change of various quantities
Marginal Cost and Marginal Revenue using derivatives
- Define marginal cost and marginal revenue
- Find marginal cost and marginal revenue
Increasing/Decreasing Functions
- Determine whether a function is increasing or decreasing
- Determine the conditions for a function to be increasing or decreasing
Maxima and Minima
- Determine critical points of the function
- Find the point(s) of local maxima and local minima and corresponding local maximum and local minimum values
- Find the absolute maximum and absolute minimum value of a function
- Solve applied problems
Integration
- Understand and determine indefinite integrals of simple functions as anti-derivative
Indefinite integrals as family of curves
Evaluate indefinite integrals of simple algebraic functions by methods of
- Substitution
- Partial Fraction
- By Parts
Definite Integral as area under the curve
- Define definite integral as area under the curve (non-trigonometric function)
- Understand fundamental theorem of integral calculus and apply it to evaluate the definite integral
- Apply properties of definite integrals to solve problems
Application of Integration
- Identify the region representing C.S. and P.S. graphically
- Apply the definite integral to find consumer surplus-producer surplus
Differential Equations
- Recognize a differential equation
- Find the order and degree of a differential equation
Formulating and solving differential equations
- Formulate differential equations
- Verify the solution of differential equation
- Solve simple differential equation
Check Out: CUET UG Total Marks
UNIT IV: Probability Distributions
Probability Distribution
- Understand the concept of Random Variables and its Probability Distributions
- Find probability distribution of discrete random variable
Mathematical Expectation
- Apply arithmetic mean of frequency distribution to find the expected value of a random variable
Variance
Calculate the Variance and S.D. of a random variable
Binomial Distribution
- Identify the Bernoulli Trials and apply Binomial Distribution
- Evaluate Mean, Variance and S.D. of a Binomial Distribution
Poisson Distribution
- Understand the conditions of Poisson Distribution
- Evaluate the Mean and Variance of Poisson distribution
Normal Distribution
- Understand normal distribution is a continuous distribution
- Evaluate value of Standard normal variate
- Area relationship between Mean and Standard Deviation
UNIT V: Time Based Data
Time Series
- Identify time series as chronological data
Components of Time Series
- Distinguish between different components of time series
Time Series Analysis for Univariate Data
- Solve practical problems based on statistical data and Interpret
Secular Trend
- Understand the long term tendency
Methods of Measuring trend
- Demonstrate the techniques of finding trend by different methods
UNIT VI: Inefrential Statistics
Population and Sample
- Define Population and Sample
- Differentiate between population and sample
- Define a representative sample from a population
- Differentiate between a representative and a non-representative sample
- Draw a representative sample using simple random sampling
- Draw a representative sample using a systematic random sampling
Parameter and Statistics and Statistical Interferences
- Define Parameter with reference to Population
- Define Statistics with reference to Sample
- Explain the relation between Parameter and Statistic
- Explain the limitation of Statistic to generalize the estimation for population
- Interpret the concept of Statistical Significance and Statistical Inferences
- Central Limit Theorem
- Explain the relation between Population-Sampling Distribution-Sample
t-Test (one sample t-test for a small group sample)
- Define a hypothesis
- Differentiate between Null and Alternate hypothesis
- Define and calculate degree of freedom
- Test Null hypothesis and make inferences using t-test statistic for one group
UNIT VII: Financial Mathematics
Perpetuity, Sinking Funds
- Explain the concept of perpetuity and sinking fund
- Calculate perpetuity
- Differentiate between sinking fund and saving account
Calculation of EMI
- Explain the concept of EMI
- Calculate EMI using various methods
Calculation of Returns, Nominal Rate of Return
- Explain the concept of rate of return and nominal rate of return
- Calculate rate of return and nominal rate of return
Compound Annual Growth Rate
- Understand the concept of Compound Annual Growth Rate
- Differentiate between Compound Annual Growth rate and Annual Growth Rate
- Calculate Compound Annual Growth Rate
Linear method of Depreciation
- Concept of linear method of Depreciation
- Interpret cost, residual value and useful life of an asset from the given information
- Depreciation
Valuation of Bonds
- Concept of bond and related terms
- Value of bond using present value approach
UNIT VIII: Linear Programming
Introduction and Related Terminology
- Familiarize with terms related to Linear Programming Problem
Mathematical formulation of Linear Programming Problem
- Formulate Linear Programming Problem
Different types of Linear Programming Problems
- Identify and formulate different types of LPP
Graphical Method of Solution for problems in two Variables
- Draw the Graph for a system of linear inequalities involving two variables and find its solution graphically.
Feasible and Infeasible Regions
- Identify feasible, infeasible and bounded regions
Feasible and infeasible solutions, optimal feasible solution
- Understand feasible and infeasible solutions
- Find optimal feasible solutions
CUET Mathematics Syllabus PDF Download
Students preparing for mathematics can downlaod the CUET Mathematics syllabus PDF from the direct link given below.
Also Download:
CUET Mathematics Question Paper
CUET UG Subjects: Question Paper & Syllabus PDFs
Download the CUET Question Paper PDFs and syllabus for Sections I, II, & III from the table below:
The difficulty level of the CUET exam varies between moderate and tough. Since the CUET UG exam is held for multiple subjects and slots, the difficulty level of the exam varies from subject to subject. Sometimes, the difficulty level may also vary for different slots. While for the well-prepared candidates, the difficulty level will be low, for the underprepared students, the level of difficulty will be on the higher side.
No, CUET syllabus is not based on CBSE syllabus as claimed by Education Ministry in Rajya Sabha. The CUET exam is designed to assess the general understandig of the candidate in subjects he/she has opted for. CUET UG is on of the biggest UG entrance exam carnival conducted for admission in cebtral, state, private and deemed universities.
Candidates preparing for CUET UG exam must check the detailed CUET syllabus and CUET question paper to become familiar with the important topics and type of questions asked in the exam.
Since the CUET UG 2025 syllabus is in line with the Class 12 Board exam syllabus, it can be safely assumed that the NCERT books are enough to clear CUET UG 2025 exam. Candidates must note that, CUET exam tests students' understanding of the concepts and ability to apply them in various situations. Therefore, to prepare well and get a good score, it is advised that students refer to other study materials and books designed for national level competitive entrance exams. The CUET UG syllabus is in tune with the Class 12 Board exam syllabus. The chapters and topics are similar to Class 12 syllabus. Unlike other UG entrance exams, CUET UG syllabus does not include Class 11 syllabus.
Also Read: CUET Previous Years' Question Papers
Best Books for CUET Mathematics Preparation
Refer to the following books to attain a good CUET score in the CUET mathematics exam.
- NCERT Class 12 Mathematics Textbook (Majority of the exam is NCERT based)
- A Text Book of Mathematics Class 12 by Pradeep
- CUET Mathematics by Arihant Experts
- Mathematics for Competitive Exams by R.S. Aggarwal
- CUET Guide for Mathematics by Oswaal
Read More:

Nupur Jain started with a passion for educational content writing, which soon grew into a meaningful journey of helping students through reliable guidance. A commerce graduate from Delhi University, she has spent ov
Read Full BioNews & Updates
Explore Other Exams
5 Jan '26 - 6 Apr '26 | NEST 2026 Application Process |
5 Jan '26 - 12 Apr '26 | NEST 2026 Application Process |
Mar '26 | IISER Aptitude Test 2026 Regis... |
Apr '26 | IISER Aptitude Test 2026 Corre... |
Jul '25 | ITM NEST 2025 Result Date |
Jun '25 | ITM NEST 2025 Exam date |
Mar '26 | OUAT Entrance Exam 2026 Form A... |
Apr '26 | OUAT Entrance Exam 2026 Form A... |
Jul '22 | DAVV CET 2022 Registration |
Dec '24 | TISSNET 2024 Mock Test |
Jun '24 | TISS Online Assessment 2024 |
Student Forum
Answered 15 hours ago
No, CUET scores are not compulsory for admissions into the BA course at Jindal School of Environment and Sustainability. The college accepts other online entrance tests/ national or international level entrance tests, such as JSAT/ SAT/ ACT. Thus, CUET is one of the accepted entrance tests for enrol
K
Contributor-Level 10
Answered 3 days ago
To prepare for CUET Mathematics exam effectively, students must ideally give two to three hours practice. Students must focus on previous year qiuestion papers and mock tests to prepare well for exam. Daily practice and consistency will help candidate score 250 marks in exam.
N
Contributor-Level 6
Answered 3 days ago
Yes, NCERT is sufficient for conceptual clarity while preparing for CUET exam, but MCQ practice and CUET mock tests are important for scoring high. Students must not only focus on preparation books, they must solve CUET previous year question papers for Mathematics to know important topics or repeat
N
Contributor-Level 6
Answered 3 days ago
No, a valid CUET score is accepted for admissions to both BA (Hons) in Liberal Arts & Humanities and the BA (Hons) in Philosophy, Politics & Economics at JSLAH.
In the previous year admissions, CUET was only listed as an accepted exam for the BA (Hons) in Liberal Arts & Humanities admission.
S
Contributor-Level 10
Answered 3 days ago
No, candidates who wish receive the Jindal School of Liberal Arts and Humanities BA (Hons) scholarships must provide a valid score in the JSAT. Those candidates who appeared for the CUET during BA (Hons) admissions can still appear for the JSAT after getting admitted into the Jindal School of Libera
S
Contributor-Level 10
Answered 3 days ago
For admission to Delhi University, candidate must have passed or appeared for class 12 examination. There are no minimum marks requirement in class 12 for DU admission through CUET UG. DU may use the class 12 marks or percentage for tie breaking criteria.
N
Contributor-Level 6
Answered 3 days ago
Class 12 marks are important for fulfilling the admission criteria and tie breaking criteria (if any) during admissions. Admission to Central Universities are conducted through CUET scores, however, candidates must fulfil the minimum marks requirement for admissions.
D
Contributor-Level 6
Answered 3 days ago
The minimum marks for CUET class 12th is prescribed differently for accepting universities. CUET universities like DU and Allahabad University does not prescribe the minimum marks in class 12 for CUET UG. However, universities like Banaras Hindu University, BBAU has prescribed the minimum percentage
N
Contributor-Level 6
Answered 3 days ago
There are a total of 157 subjects in the CUET PG exam. The subjects are segregated into six streams. The table below shows the number of papers in each stream.
| Stream | Number of Subjects or Papers |
|---|---|
| Science | 30 |
| MTech | 12 |
| Language | 41 |
| Humanities | 26 |
| Common | 22 |
| Acharya | 26 |
The CUET PG exam pattern is the same for each paper. The language of the CUET PG question papers is English and Hindi. For the Language paper
P
Beginner-Level 5
Answered a week ago
Yes, there is a scholarship for BSc students at IILM University Greater Noida based on the CUET percentile.
If you score 95 percentile or more, you get a 40% scholarship.
In case your percentile is between 90 to 94.99, you get a 30% scholarship.
For the 80 to 89.99 percentile, a 20% scholarship is of
J
Contributor-Level 10
 Registration - 3 Jan '26 - 30 Jan '26
Registration - 3 Jan '26 - 30 Jan '26



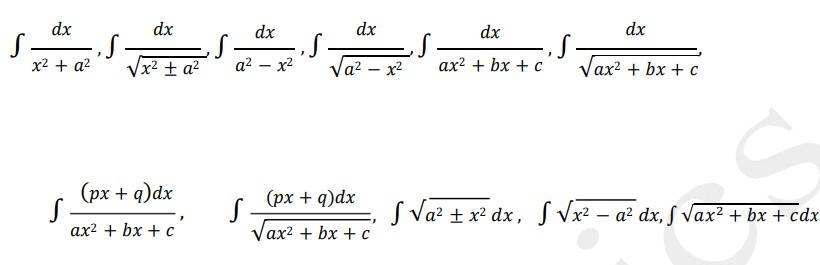


Yes, CUET UG 2026 official syllabus has been released. NTA uploaded the CUET 2026 syllabus PDFs online at cuet.nta.nic.in. Candidates preparing for CUET 2026 exam can download the CUET syllabus. The CUET syllabus is based on class 12th NCERT curriculum. Candidates must prepare well from the class 12th syllabus to ace the entrance examination.